美团笔试-后端 2022.9.17

编程题2：组队

时间限制：3000MS
内存限制：589824KB
题目描述：
小团所在的游戏工会最近接到了许多相同的任务。每个任务都需要两位玩家组队参与。设组队的两个玩家的等级分别为a和b，则a+b必须大于等于x且a*b必须大于等于y。现在小团想知道在工会内部由多少合法的组队方式。

输入描述

第一行有三个正整数n, x, y(2<=n<=100000, 1<=x,y<=1000000)，分别代表工会中的玩家数，组队玩家等级> 之和的下限，组队玩家等级之积的下限。
第二行有n个数，第i个代表工会中第i个玩家的等级。
等级均为不超过1000的整数。
数字间两两有空格隔开。

输出描述

输出一个非负整数，代表所求的答案，即有多少种合法的组队方式。

样例输入

5 6 3
3 4 2 5 1

样例输出

5

提示

(2, 4) (2, 5) (3, 4) (3, 5) (4, 5)为可行的五种组队方案。

# 排序+二分查找，不保证结果是对的
n, x, y = map(int, input().split())
data = list(map(int, input().split()))data.sort()def find_first_idx(target):if data[-1]=target:r = midelse:l = mid+1return lans = 0
j = n-1cache = set()
for i in range(n):v1 = x-data[i]v2 = y/data[i]idx1 = find_first_idx(v1)idx2 = find_first_idx(v2)idx = max(idx1, idx2)if (i, idx) not in cache and (idx, i) not in cache:ans += n-idxif idx<=i:ans -= 1cache.add((i, idx))cache.add((idx, i))print(ans)

编程题3：魔法筒

时间限制：3000MS
内存限制：589824KB
题目描述：
小团有n个球，编号为1到n，有一天，这n个球掉进了两个魔法筒里面。每个魔法筒可以视为一个栈，即按顺序掉进去的球只能以逆序取出来，魔法筒上面附有的魔法使得小团每次只能从筒的顶端拿走当前仍在两个筒中的编号最小的球，或者将顶端的球放入另一个魔法筒。现在小团想知道他至少要操作多少次才能将所有球都从筒中取出。每次操作即从筒中拿出一个球或将一个球从一个筒的顶端移入另一个筒。

输入描述

第一行有三个正整数n, x, y(2<=n<=1000，1<=x,y<=n-1,x+y=n)，分别代表球的总数，第一个筒中的球数和第二个筒中的球数。
第二行有x个数，依次代表第一个筒中从底端到顶端的x个球。
第二行有y个数，依次代表第二个筒中从底端到顶端的x个球。
保证编号为1到n的每个球均恰好在一个筒中出现。

输出描述

输出一个非负整数，代表所求的答案。

样例输入

5 2 3
3 4
2 5 1

样例输出

8

提示

先将1号球取出，将5号球放入第一个筒，取出2号球，然后将第一个筒中的5号球和4号球一次倒入第二个筒，取出3号球，然后取出第二个筒中的4号球和5号球，共8次操作。

# 直接模拟
n, x, y = map(int, input().split())
dx = list(map(int, input().split()))
dy = list(map(int, input().split()))val = 1ans = 0
while dx or dy:if val in dx:idx = dx.index(val)ans += len(dx)-idxfor _ in range(idx+1, len(dx)):dy.append(dx.pop())dx.pop()else:idx = dy.index(val)ans += len(dy)-idxfor _ in range(idx+1, len(dy)):dx.append(dy.pop())dy.pop()val += 1
print(ans)

编程题4：排序

时间限制：3000MS
内存限制：589824KB
题目描述：
小美有n个蓝色的球，上边分别写着1到n。小团有n个红色的球，上边也写着1到n。有一天，神秘人把这2n个球混到了一起并排成一列。在将这2n个球分开之前，小美和小团必须通过数次“交换相邻的两个球”的操作使得任意两个分别写着i和i+1的同色球，有i在i+1左边。现在小美和小团想知道它们需要进行多少次操作才能达到条件。

输入描述

第一行有一个正整数n(1<=n<=200)，代表球的个数。
第二行有2n个整数，代表从左到右的2n个球。整数代表红球，负数代表篮球。-n到n之间的每个非零整数均会出现恰好一次。

输出描述

输出一个非负整数，代表所求的答案。

样例输入

4
3 -3 1 -4 2 -2 -1 4

样例输出

10

提示

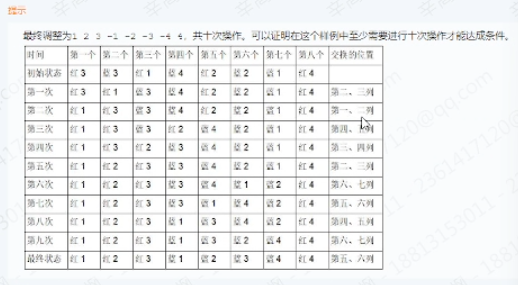
太难了，目前没时间看，有一个参考题解http://t.zoukankan.com/Aragaki-p-9031848.html

编程题5：小树

时间限制：3000MS
内存限制：589824KB
题目描述：
小美有一颗树，她想知道这棵树是不是一颗正常的小树。小美认为小树是正常的有这样的条件：可以给定树选定一个跟P，如果任意一个节点的值均比儿子节点的值的最小值小（如果有儿子的话）。
树是一种无向无环联通图。如果节点x到树根P的最短路径上需要经过的第一个点是y，那么x是y的儿子。跟P不是任何节点的儿子。

输入描述

多组数据，数据开头一个数T表示数据组成。
对于每组数据：
第一行一个正整数n，表示树上节点数。
接下来一行n-1个数 a 1 , a 2 , . . . , a n − 1 a_1,a_2,...,a_{n-1} a1​,a2​,...,an−1​。
接下来一行n-1个数 b 1 , b 2 , . . . , b n − 1 b_1,b_2,...,b_{n-1} b1​,b2​,...,bn−1​。
其中（ a i , b j a_i,b_j ai​,bj​）表示节点 a i a_i ai​与 b j b_j bj​相连，保证是一颗合法的树。
接下来一行n个数 v 1 , v 2 , . . . , v n v_1,v_2,...,v_n v1​,v2​,...,vn​表示节点i的值为 v i v_i vi​。
数字间两两有空格隔开。
1<=n<=50000，1<= a i , b j a_i,b_j ai​,bj​<=n，1<= v i v_i vi​<= 1 0 9 10^9 109，1<=T<=5

输出描述

对每组数据一行一个整数表示答案，如果不存在这样的根输出-1，否则输出树根的节点编号。

样例输入

2
3
1 1
2 3
1 1 2
3
1 1
2 3
1 2 3

样例输出

-1
1

import copyt = int(input())while t>0:t -= 1n = int(input())nodes = [[] for _ in range(n)]for _ in range(n-1):a, b = map(int, input().split())nodes[a-1].append(b-1)nodes[b-1].append(a-1)vals = list(map(int, input().split()))minorder = 0flag = Truefor i in range(1, n):if vals[minorder]==vals[i]:flag = Falseelif vals[minorder]>vals[i]:minorder = iflag = Truevis = [False]*ndef dfs(node):vis[node] = Truecur_val = vals[node]ch_min_val = float('inf')for ch in nodes[node]:if not vis[ch]:ch_val = dfs(ch)ch_min_val = min(ch_val, ch_min_val)if cur_val>=ch_min_val:return -1else:return cur_valif not flag:print(-1)else:res = dfs(minorder)if res==-1:print(-1)else:print(minorder+1)

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！