一 问题描述

用一个二维数组表示一个迷宫，其中 1 表示墙壁，0 表示可以走的路，只能横着走或竖着走，不能斜着走，编写程序，找出从左上角到右下角的最短路径。

int maze[5][5] = {

    0, 1, 0, 0, 0,

    0, 1, 0, 1, 0,

    0, 0, 0, 0, 0,

    0, 1, 1, 1, 0,

    0, 0, 0, 1, 0,

};

二 输入和输出

1 输入

一个 5 × 5 的二维数组，表示一个迷宫。数据保证有唯一解。

2 输出

左上角到右下角的最短路径。

三 输入和输出样例

1 输入样例

0 1 0 0 0

0 1 0 1 0

0 0 0 0 0

0 1 1 1 0

0 0 0 1 0

2 输出样例

(0, 0)

(1, 0)

(2, 0)

(2, 1)

(2, 2)

(2, 3)

(2, 4)

(3, 4)

(4, 4)

四 算法设计

可以使用广度优先搜索解决。定义方向数组 dir[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}

1 定义一个队列，将起点（0,0）入队，标记已走过。

2 如果队列不空，则队列出队。

3 如果队头正好是目标（4,4），则退出。

4 沿着 4 个方向搜索，如果该节点未出边界，未走过且不是墙壁，则标记走过并入队，用前驱数组记录该节点。

5 转向步骤 2。

6 根据前驱数组输出从起点到终点的最短路径。

五 代码

package com.platform.modules.alg.alglib.poj3984;import java.util.LinkedList;
import java.util.Queue;public class Poj3984 {boolean mp[][] = new boolean[5][5];boolean vis[][] = new boolean[5][5];int dir[][] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};public String output = "";private node pre[][] = new node[10][10];public Poj3984() {for (int i = 0; i < 10; i++) {for (int j = 0; j < 10; j++) {pre[i][j] = new node();}}}public String cal(String input) {String[] line = input.split("\n");for (int i = 0; i < 5; i++) {String[] words = line[i].split(" ");for (int j = 0; j < 5; j++) {mp[i][j] = words[j].equals("1");}}bfs();node ed = new node();ed.x = ed.y = 4;print(ed);return output;}void bfs() {Queue que = new LinkedList<>(); // 创建一个普通队列(先进先出)node st = new node();st.x = 0;st.y = 0;que.add(st);vis[0][0] = true;while (!que.isEmpty()) {node now = que.peek();que.poll();if (now.x == 4 && now.y == 4)return;for (int i = 0; i < 4; i++) {node next = new node();next.x = now.x + dir[i][0];next.y = now.y + dir[i][1];if (next.x >= 0 && next.x < 5 && next.y >= 0 && next.y < 5 && !mp[next.x][next.y] && !vis[next.x][next.y]) {vis[next.x][next.y] = true;que.add(next);pre[next.x][next.y] = now;}}}}void print(node cur) {if (cur.x == 0 && cur.y == 0) {output += "(0,0)\n";return;}print(pre[cur.x][cur.y]); // 逆序输出output += "(" + cur.x + "," + cur.y + ")\n";}
}class node {int x;int y;
}

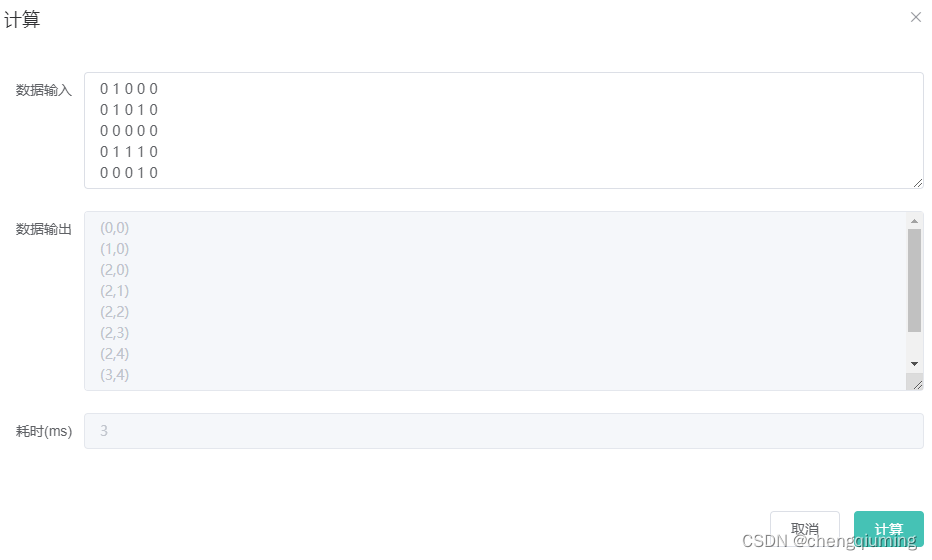
六 测试

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！