最小二乘法求解一元线性回归

最小二乘法求解一元线性回归

介绍线性回归模型以及简单一元线性回归模型的解法。

通过代码实现最小二乘法求解一元线性回归实例，并对结果进行预测。

一、线性回归

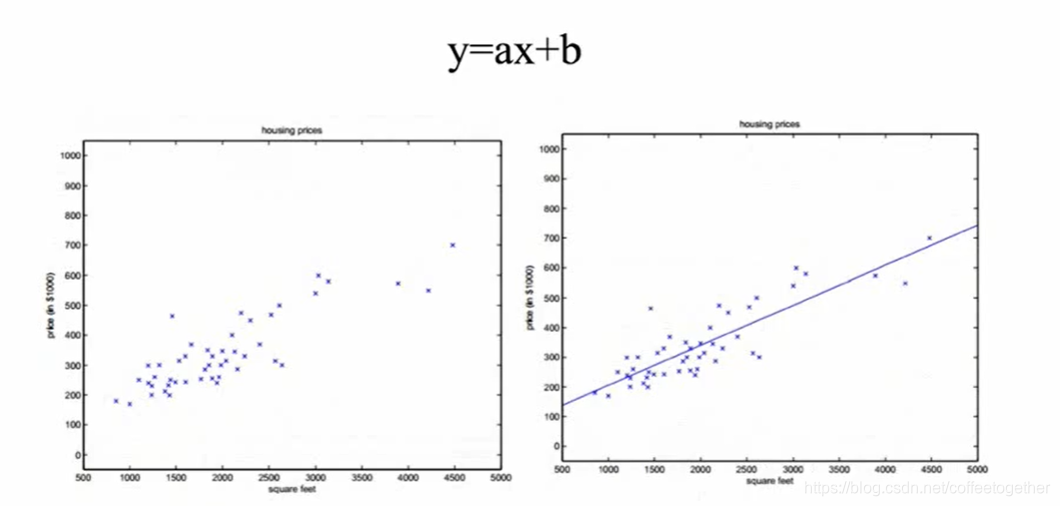
二、回归问题的解决

三、最小二乘法介绍

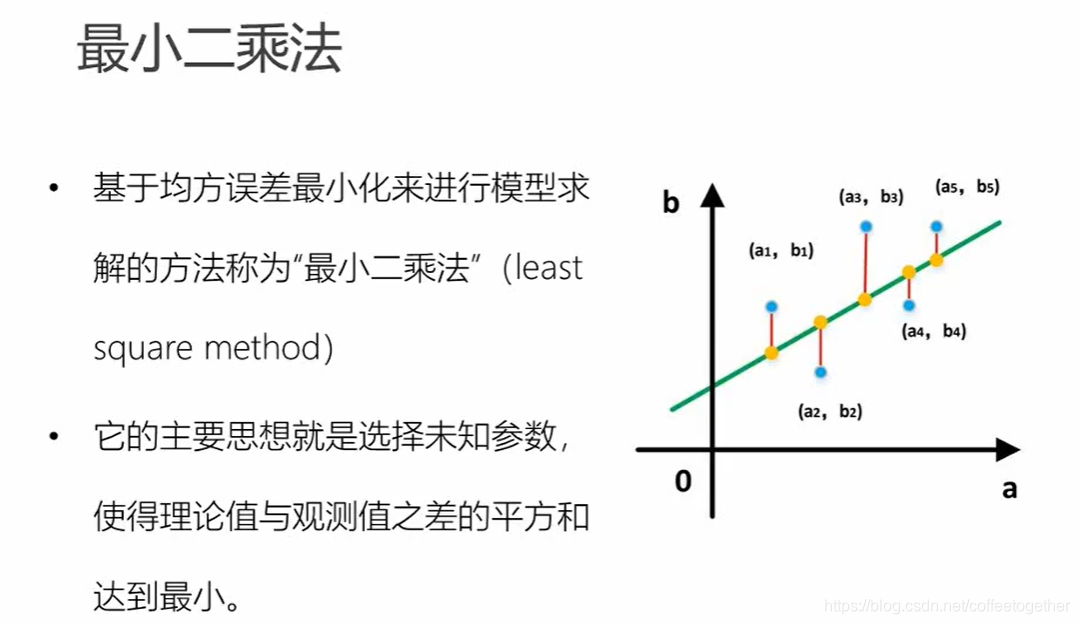
四、最小二乘法求解线性回归

五、实例验证

案例背景：数据中参数x为学习时间，y为得分。通过最小二乘法求解参数w，b，均方差。并预测x=80时的得分。

数据链接：
链接: https://pan.baidu.com/s/1KVw_9O5o9vqQnpgRNfLGVQ
提取码：8u8e

1.导入数据

# 导入必要库
import numpy as np
import matplotlib.pyplot as plt

points = np.genfromtxt('E:/PythonData/machine_learning/data.csv',delimiter=',')# 查看前5行数据
points[:5]

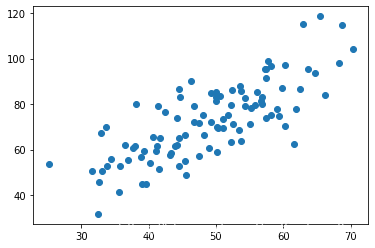
2.绘制散点图

# 分别提取points中的x和y数据
x = points[:,0]
y = points[:,1]# 绘制散点图
plt.scatter(x,y)
plt.show()

3.定义损失函数

# 损失函数是系数w，b的函数，另外还要传入数据x，y
def computer_cost(w,b,points):total_cost = 0M = len(points)# 逐点计算平方损失误差，然后求平均数for i in range(M):x = points[i,0]y = points[i,1]total_cost +=(y - w *x - b)**2# 取平均return total_cost/M

4.定义算法拟合函数

# 先定义求均值函数
def average(data):sum = 0num = len(data)for i in range(num):sum+=data[i]return sum/num# 定义核心拟合函数
def fit(points):M = len(points)x_bar = average(points[:,0])sum_yx = 0sum_x2 = 0sum_delta = 0for i in range(M):x = points[i,0]y = points[i,1]sum_yx += y*(x-x_bar)sum_x2 += x**2# 根据公式计算ww = sum_yx/(sum_x2 - M*(x_bar**2))# 再次创建for循环计算bfor i in range(M):x = points[i,0]y = points[i,1]sum_delta += y-w*xb = sum_delta/Mreturn w,b 

5.测试（得到参数w，b，均方误差）

# 将测试集传入拟合函数中
w,b = fit(points)
print('w is :',w)
print('b is :',b)cost = computer_cost(w,b,points)
print('cost is ',cost)

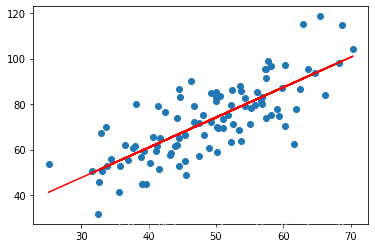
6.绘制拟合曲线

plt.scatter(x,y)# 针对每一个x，绘制出预测的值
pred_y = w*x+b# 画出拟合曲线，颜色设置为红色
plt.plot(x,pred_y,c='r')

7.预测分数

# 给出参数x，得出预测结果
pred_y1 = w*80+b
print(pred_y1)

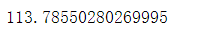
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！