一、实验目的与要求：

（一）实验目的

1、掌握图形结构的（邻接矩阵）输入方法

2、掌握图形结构的说明、创建以及图的存储表示

3、掌握最短路径算法原理

4、掌握最短路径的实现方法

（二）实验要求

1、熟悉C/C++语言编程

2、熟练使用C/C++语言实现图形结构的说明、创建以及图的存储表示

二、实验内容：

校园导航问题

（一）问题描述：

设计校园的平面图，至少包括8个以上的场所，每两个场所间可以有不同的路，且路长也可能不同。

1.（必做）找出从一个场所出发到达其它所有场所的最佳路径（最短路径）。

2.（选做）找出从任意场所到达另一场所的最佳路径（最短路径）。

（二） 基本要求

1、设计校园平面图，在校园景点选8个以上的景点。以图中顶点表示校园内各景点，存放景点名称、代号、简介等信息；以边表示路径，存放路径长度等有关信息。

2、为来访客人提供图中任意景点相关信息的查询。

3、为来访客人提供任意景点的问路查询。

（如：从学校1号门到各景点的最佳路线及距离；主楼到湖边餐厅的最佳路线及距离。）

4、界面要求：有合理提示；每个功能可以设立菜单；根据提示，可以完成相关的功能要求

3、熟练应用图形数据结构编程实现最短路径的算法

三、实验步骤与过程：

[介绍实验过程、算法描述及解题思路等]

[实验代码清单(要有注释语句)]

实验过程：

    先对实验要求进行一个脑中的呈现。如：输出格式，菜单页面，所需算法等等。再根据所想的算法进行代码实现。最后，对输出格式进行修改及完善即可。

算法描述：

  Dijkstra算法是一个基于「贪心」、「广度优先搜索」、「动态规划」求一个图中一个点到其他所有点的最短路径的算法，时间复杂度O(n^2)。 （可以解决问题一）

  Floyd算法是一个基于「贪心」、「动态规划」求一个图中所有点到所有点最短路径的算法，时间复杂度O(n^3)。（可以解决问题二）

解题思路：

  看到第一问和第二问就很容易想到了Dijkstra算法和Floyd算法去实现，所以就去实现这个两个算法即可。

代码呈现：

功能一：对各个场所进行简单描述

注：对于这个其实也可以创建一个顶点的结构体，包含char str[MAX]去存放场所信息。

//各个场所的功能函数
void feature()
{hint();printf("请输入场所编号: ");int num;scanf("%d",&num);switch (num) {case 1:printf("宿舍有公共厨房，公共阅览室，公共厕所\n\n");break;		case 2:printf("一食堂有丰富的菜品\n\n");break;	case 3:printf("湖滨餐厅有中西方菜品\n\n");break;	case 4:printf("图书馆设施好，学习氛围浓烈\n\n");break;	case 5:printf("实验楼有实验室以及机房\n\n");break;			case 6:printf("可以在里面举办一些晚会\n\n");break;	case 7:printf("老师办公区域\n\n");break;	case 8:printf("看主楼的最好位置\n\n");break;	default:printf("无该场所编号，请重新输入场所编号\n\n");break;		}
}

功能二：找出从一个场所出发到达其它所有场所的最佳路径（dilkstra算法）

//取最小值的函数 
int getMin(int* d,int* s,Graph* G)
{int min=MAX;int index;for(int i=0;ivexNum;i++){if(!s[i] && d[i]vexNum); int* p=(int*)malloc(sizeof(int)*G->vexNum);int* d=(int*)malloc(sizeof(int)*G->vexNum);//对辅助数组进行初始化 for(int i=0;ivexNum;i++){if(G->arcs[index][i]>0 && G->arcs[index][i]!=MAX){d[i]=G->arcs[index][i];p[i]=index;}else{d[i]=MAX;p[i]=-1;}if(i==index){s[i]=1;d[i]=0;}else{s[i]=0;}}  for(int i=0;ivexNum-1;i++){int index=getMin(d,s,G);s[index]=1;		//代表已经找到了最小路径 for(int j=0;jvexNum;j++){if(!s[j] && d[index]+G->arcs[index][j]arcs[index][j];	 p[j]=index;		//更改 }} }//输出到达个点的最短路径 for(int i=0;i<=G->vexNum-1;i++){int j=i;printf("%s <—— ",G->vexs[i].name);	//最后打印所到场所while(j!=index){j=p[j];if(j!=index){printf("%s <——  ",G->vexs[j].name);	}}  	 printf("%s",G->vexs[index].name);printf("\n%s --> %s的最短路径大小为：%d分钟",G->vexs[index].name,G->vexs[i].name,d[i]);printf("\n");}
}

功能三：找出从一个场所出发到达其它所有场所的最佳路径（floyd算法）

/*floyd算法(3 for:[n*n*n]):求每一对顶点之间的最短路径d数组:保存了两点的最短路径长度(权值)p数组:保存了两点之间最短路径前驱核心:试探法，通过加入不同的点进行中转，选择出最优解
*/
void floyd(Graph* G,int f,int n)
{int d[G->vexNum][G->vexNum];int p[G->vexNum][G->vexNum];//数组的初始化for(int i=0;ivexNum;i++){for(int j=0;jvexNum;j++){d[i][j]=G->arcs[i][j];if(G->arcs[i][j]>0 && G->arcs[i][j]!=MAX)	//两个顶点之间有弧{p[i][j]=i;	//有弧指向前继顶点}else{p[i][j]=-1;}}}/*进行试探法:第一个循环代表着加入的顶点进行试探后两个循环代表着每一对顶点*/for(int i=0;ivexNum;i++){for(int j=0;jvexNum;j++){for(int k=0;kvexNum;k++){if(d[j][i]+d[i][k] %s的最小路径为：%d分钟\n",G->vexs[f].name,G->vexs[n].name,d[f][n]);int l=p[f][n];  // l作为中间变量用来接受最短路径中的父亲节点 printf("最短路径为:  %s",G->vexs[f].name);   // 输出最短路径 int temp=0;		//创建一个中间变量，便于储存l值while(l!=f)  {printf(" --> %s",G->vexs[l].name);if(l==temp)		//当后一个l等于前一个l时，循环截至break;l=p[l][n];  //  不断更新l节点 temp=l;}printf(" --> %s\n\n",G->vexs[n].name);}

完整代码：

#include
#include
#include
#include/*图顶点之间不通，那么邻接矩阵的值为MAX如果顶点是自己本身，那么值为0*/
#define MAX 32767int system(const char *command);////结构体定义顶点
typedef struct Vertex  
{int num;  //顶点编号 char name[MAX];  //顶点名称 
}Vertex;     typedef struct Graph{Vertex vexs[9];		//顶点int** arcs;		//权重(使用**目的表示矩阵)int vexNum;int arcsNum;
}Graph;//初始化一个图
Graph* initGraph(int vexNum)
{Graph* G=(Graph*)malloc(sizeof(Graph));G->arcs=(int**)malloc(sizeof(int*) *vexNum);for(int i=0;iarcs[i]=(int*)malloc(sizeof(int) *vexNum);}for(int i=1;i<=G->vexNum;i++) G->vexs[i].num=i;    //初始化顶点编号为1-10 G->vexNum=vexNum;G->arcsNum=0;strcpy(G->vexs[0].name,"宿舍");strcpy(G->vexs[1].name,"一食堂");strcpy(G->vexs[2].name,"湖滨餐厅");strcpy(G->vexs[3].name,"图书馆");strcpy(G->vexs[4].name,"二号实验楼");strcpy(G->vexs[5].name,"礼堂");strcpy(G->vexs[6].name,"主楼");strcpy(G->vexs[7].name,"一号门");return G;
}//构建一个图
void createGraph(Graph* G,int* arcs)
{for(int i=0;ivexNum;i++){for(int j=0;jvexNum;j++){G->arcs[i][j]=*(arcs+i*G->vexNum+j);if(G->arcs[i][j]!=0&&G->arcs[i][j]!=MAX){G->arcsNum++;}}}G->arcsNum=G->arcsNum/2;
}//取最小值的函数 
int getMin(int* d,int* s,Graph* G)
{int min=MAX;int index;for(int i=0;ivexNum;i++){if(!s[i] && d[i]vexNum); int* p=(int*)malloc(sizeof(int)*G->vexNum);int* d=(int*)malloc(sizeof(int)*G->vexNum);//对辅助数组进行初始化 for(int i=0;ivexNum;i++){if(G->arcs[index][i]>0 && G->arcs[index][i]!=MAX){d[i]=G->arcs[index][i];p[i]=index;}else{d[i]=MAX;p[i]=-1;}if(i==index){s[i]=1;d[i]=0;}else{s[i]=0;}}  for(int i=0;ivexNum-1;i++){int index=getMin(d,s,G);s[index]=1;		//代表已经找到了最小路径 for(int j=0;jvexNum;j++){if(!s[j] && d[index]+G->arcs[index][j]arcs[index][j];	 p[j]=index;		//更改 }} }//输出到达个点的最短路径 for(int i=0;i<=G->vexNum-1;i++){int j=i;printf("%s <—— ",G->vexs[i].name);	//最后打印所到场所while(j!=index){j=p[j];if(j!=index){printf("%s <——  ",G->vexs[j].name);	}}  	 printf("%s",G->vexs[index].name);printf("\n%s --> %s的最短路径大小为：%d分钟",G->vexs[index].name,G->vexs[i].name,d[i]);printf("\n");}
}/*floyd算法(3 for:[n*n*n]):求每一对顶点之间的最短路径d数组:保存了两点的最短路径长度(权值)p数组:保存了两点之间最短路径前驱核心:试探法，通过加入不同的点进行中转，选择出最优解
*/
void floyd(Graph* G,int f,int n)
{int d[G->vexNum][G->vexNum];int p[G->vexNum][G->vexNum];//数组的初始化for(int i=0;ivexNum;i++){for(int j=0;jvexNum;j++){d[i][j]=G->arcs[i][j];if(G->arcs[i][j]>0 && G->arcs[i][j]!=MAX)	//两个顶点之间有弧{p[i][j]=i;	//有弧指向前继顶点}else{p[i][j]=-1;}}}/*进行试探法:第一个循环代表着加入的顶点进行试探后两个循环代表着每一对顶点*/for(int i=0;ivexNum;i++){for(int j=0;jvexNum;j++){for(int k=0;kvexNum;k++){if(d[j][i]+d[i][k] %s的最小路径为：%d分钟\n",G->vexs[f].name,G->vexs[n].name,d[f][n]);int l=p[f][n];  // l作为中间变量用来接受最短路径中的父亲节点 printf("最短路径为:  %s",G->vexs[f].name);   // 输出最短路径 int temp=0;		//创建一个中间变量，便于储存l值while(l!=f)  {printf(" --> %s",G->vexs[l].name);if(l==temp)		//当后一个l等于前一个l时，循环截至break;l=p[l][n];  //  不断更新l节点 temp=l;}printf(" --> %s\n\n",G->vexs[n].name);}void menu()
{printf("**************************************************************\n");printf("		深圳北理莫斯科大学校园导航         	          \n");printf("**************************************************************\n");printf("****  1.查询找出从一个场所出发到达其它所有场所的最佳路径  ****\n");printf("****  2.查询找出从任意场所到达另一场所的最佳路径          ****\n");printf("****  3.查询各个场所的功能                                ****\n");printf("****  4.清屏                            				  ****\n");printf("****  0.退出程序                                          ****\n");printf("**************************************************************\n");
}void hint()
{printf("1-宿舍        2-一食堂  3-湖滨餐厅  4-图书馆\n");printf("5-二号实验楼  6-礼堂    7-主楼      8-一号门\n");
}//各个场所的功能函数
void feature()
{hint();printf("请输入场所编号: ");int num;scanf("%d",&num);switch (num) {case 1:printf("宿舍有公共厨房，公共阅览室，公共厕所\n\n");break;		case 2:printf("一食堂有丰富的菜品\n\n");break;	case 3:printf("湖滨餐厅有中西方菜品\n\n");break;	case 4:printf("图书馆设施好，学习氛围浓烈\n\n");break;	case 5:printf("实验楼有实验室以及机房\n\n");break;			case 6:printf("可以在里面举办一些晚会\n\n");break;	case 7:printf("老师办公区域\n\n");break;	case 8:printf("看主楼的最好位置\n\n");break;	default:printf("无该场所编号，请重新输入场所编号\n\n");break;		}
}int main()
{//打印学校图(注：需要把照片与代码放在用一个文件夹下)char pic_name[80]="school.PNG";char cmd[100];sprintf(cmd,pic_name);system(cmd);Graph* G=initGraph(8);int arcs[8][8]={	//邻接矩阵(权重(按走到该建筑的时间创立))0,3,6,6,10,5,MAX,4,3,0,4,MAX,MAX,MAX,MAX,MAX,6,4,0,1,6,MAX,MAX,MAX,6,MAX,1,0,5,MAX,MAX,MAX,10,MAX,6,5,0,MAX,3,MAX,5,MAX,MAX,MAX,MAX,0,1,2,MAX,MAX,MAX,MAX,3,1,0,1,4,MAX,MAX,MAX,MAX,2,1,0};printf("学校的平面图为:\n");createGraph(G,(int*)arcs);int input;do{Sleep(1000);	//延迟输出1s,方便查看menu();printf("请输入所需要的功能: ");scanf("%d",&input);switch (input) {case 1:{	int n;hint();	printf("请输入场所编号: ");scanf("%d",&n);if(n<1||n>8){printf("无该场所编号，请重新输入\n\n");break;}printf("\n从该场所到各个场所的最短路径依次是:\n");dijkstra(G,n-1);printf("\n");		break;}case 2:{int a,b;hint();	printf("请输入想从哪个场所到哪个场所的编号\n");printf("开始场所: ");scanf("%d",&a);printf("目的地场所: ");scanf("%d",&b);if((a<1||a>8)&&(b<1||b>8)){printf("无该场所编号，请重新输入\n\n");break;}floyd(G,a-1,b-1);			break;	}case 3:{	feature();break;}case 4:{system("cls");break;}case 0:{printf("退出程序\n");break;}default:{	printf("无该功能，请重新输入所需的功能\n\n");		break;}}}while(input);	return 0;
}

四、实验结果及数据处理分析： 

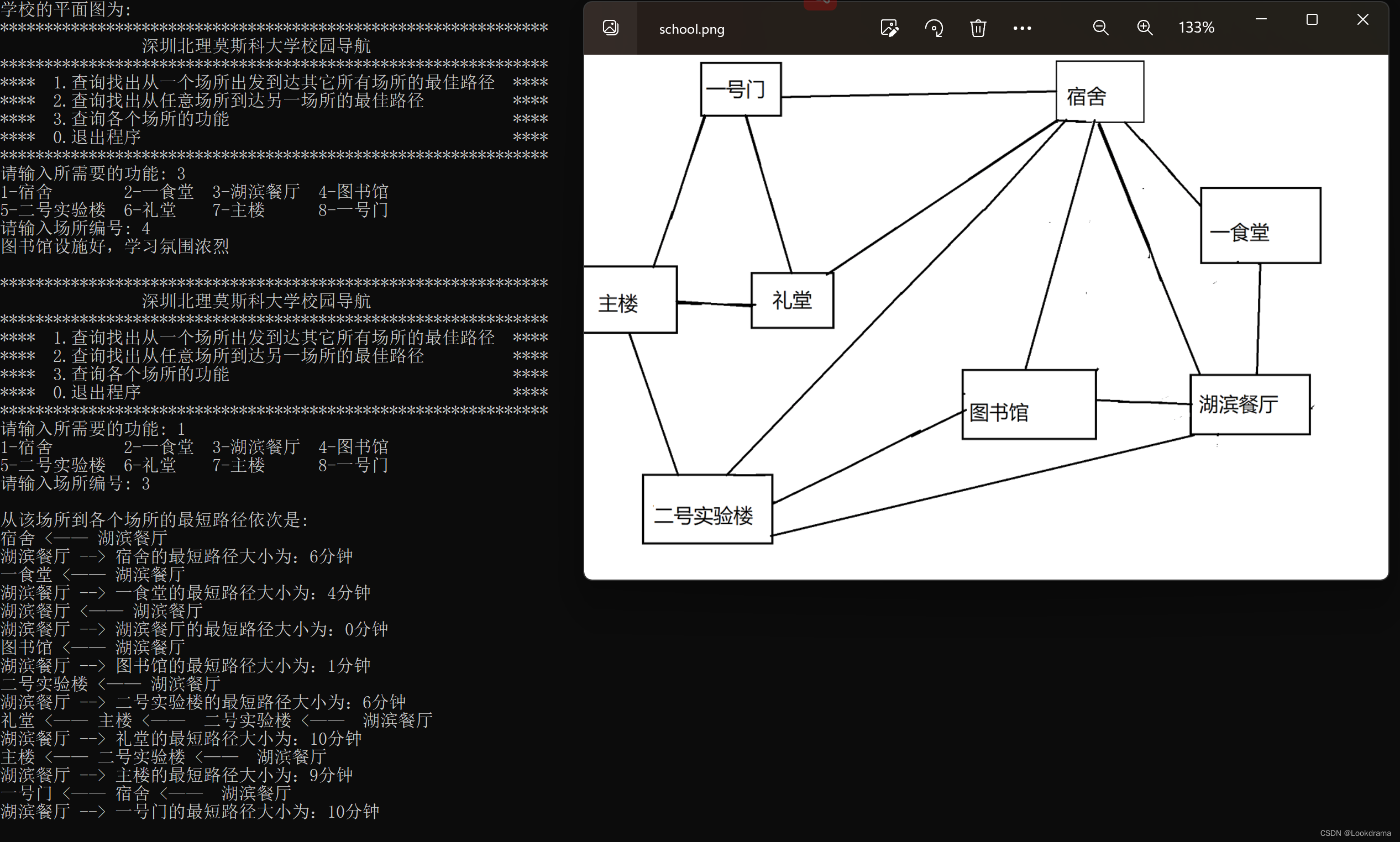
    根据运行结果，发现此代码实现了该实验的功能。(为了更好的呈现结果这里将清屏功能删除，在实际代码中可实现清屏功能。) 

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！