活动选择问题-最大场次和最大收益(贪心和动态规划求解)
一、问题描述

拓展:假如每个活动都有收益,收益各不相同,问怎样使收益最大呢?
二、求解过程分析
重要数据结构:
int p[N]; //p[i]代表在ai开始前最后结束的活动
int rec[N]; //记录决策
double dp[N]; //动态规划数组,dp[i] 代表选择第i个活动所获得的收益//dp[p[i]] 代表 选择该活动上一个最先结束的活动 时所获得的收益//状态转移方程为:dp[i] = max(dp[p[i]] + actList[i].value, dp[i - 1])
-
已证明优先选择最早结束的活动时举办活动的场次最多,证明略。那我们只需将各活动按照结束时间升序排序(使用快速排序),然后将第一个活动加入集合S(表示选择的活动),因为第一个活动一定最早结束的,再依次比较下一个活动的开始时间是否大于当前选择活动的结束时间:
struct actTime S[N]; //选择的活动集合 int res = 1; //活动场数 int k = 1; //当前活动 S[1] = actList[1]; //将第一个活动加入已选择活动集合 for(int i = 2; i <= n; i ++){if(actList[i].startTime >= actList[k].endTime){ //该场的开始时间大于上一场的结束时间 S[++ res] = actList[i]; //将该场活动加入集合 k = i; //更新当前的活动场次 }} -
使用二分法查找第i个活动前最后结束的活动
p[1] = 0; //第一个活动前没有活动 for(int i = 2; i <= n; i ++){ //依次查找活动的p[i] int time = actList[i].startTime;int l = 1, r = n;while(l < r){int mid = l + r + 1 >> 1;if(actList[mid].endTime < time) l = mid;else r = mid - 1;}//找到后赋值 p[i] = r; //l 和 r 都可 } -
动态规划
对于第i个活动,我们的选择有 选 与 不选
选:
dp[i] = dp[p[i]] + actList[i].value不选:
dp[i] = dp[i - 1]for(int i = 1; i <= n; i ++){if(dp[p[i]] + actList[i].value > dp[i - 1]){ //选择dp[i] = dp[p[i]] + actList[i].value;rec[i] = 1; //记录决策 选择 } else{ //不选 dp[i] = dp[i - 1]; }}
三、算法步骤
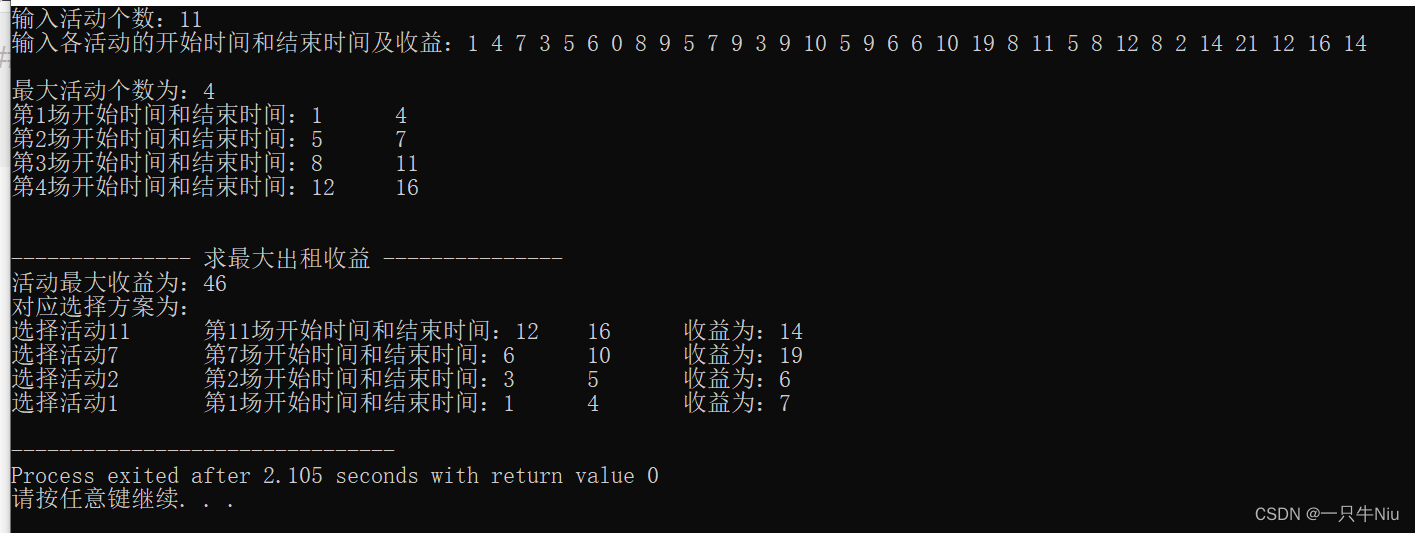
测试用例
11
1 4 7 3 5 6 0 8 9 5 7 9 3 9 10 5 9 6 6 10 19 8 11 5 8 12 8 2 14 21 12 16 14
完整代码:
#include
#include
#includeusing namespace std;/**//求场地最多能举办几场活动,分别是哪些活动 1.先用将活动按结束时间进行升序排序 -- 归并排序 //拓展:求如何选择活动带来的收益最大 2.二分查找法求解p[i] 3.再用动态规划选择活动
*/ const int N = 10010;
int n; //活动个数
int p[N]; //p[i]代表在ai开始前最后结束的活动
int rec[N]; //记录决策
double dp[N]; //动态规划数组,dp[i] 代表选择第i个活动所获得的收益//dp[p[i]] 代表 选择该活动上一个最先结束的活动 时所获得的收益//状态转移方程为:dp[i] = max(dp[p[i]] + actList[i].value, dp[i - 1])//活动时间数据结构
struct actTime{double startTime; //活动开始时间 double endTime; //活动结束时间 double value = 0; //活动的收益 void swap(actTime &a){ //交换函数 actTime b;b.endTime = this->endTime;b.startTime = this->startTime;b.value = this->value; this->endTime = a.endTime, this->startTime = a.startTime, this->value = a.value;a.endTime = b.endTime, a.startTime = b.startTime, a.value = b.value;}
};
struct actTime actList[N]; //活动信息列表 //快速排序
void quick_sort(actTime *actList, int l, int r)
{if(l >= r) return;//x:选取一个作哨兵 int x = actList[l].endTime;int i = l - 1, j = r + 1;//将 >= actList[l].endTime的都放在右边//将 <= actList[l].endTime的都放在左边while(i < j){do{i ++;}while(actList[i].endTime < x);do{j --;} while(actList[j].endTime > x);if(i < j) actList[i].swap(actList[j]);}quick_sort(actList, l, j);quick_sort(actList, j + 1, r);}//主函数
int main()
{//输入cout << "输入活动个数:";cin >> n;cout << "输入各活动的开始时间和结束时间及收益:";for(int i = 1; i <= n; i ++){cin >> actList[i].startTime >> actList[i].endTime >> actList[i].value; }cout<= actList[k].endTime){ //该场的开始时间大于上一场的结束时间 S[++ res] = actList[i]; //将该场活动加入集合 k = i; //更新当前的活动场次 }}cout << "最大活动个数为:" << res << endl;for(int i = 1; i <= res; i ++){cout << "第" << i << "场开始时间和结束时间:" <> 1;if(actList[mid].endTime < time) l = mid;else r = mid - 1;}//找到后赋值 p[i] = r; //l 和 r 都可 } //动态规划求最大收益 for(int i = 1; i <= n; i ++){if(dp[p[i]] + actList[i].value > dp[i - 1]){ //选择dp[i] = dp[p[i]] + actList[i].value;rec[i] = 1; //记录决策 选择 } else{ //不选 dp[i] = dp[i - 1]; }} //输出cout << "活动最大收益为:" << dp[n] << endl;cout << "对应选择方案为:" < 0){if(rec[k] == 1){cout << "选择活动" << k << "\t第" << k << "场开始时间和结束时间:" < 运行截图:
四、复杂性分析
快速排序:O(nlogn)
二分查找:O(nlogn)
动态规划:O(n)
输出方案:O(n)
时间复杂度为:O(nlogn)
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!