【计算机图形学|直线生成算法】中点画线法
文章目录
- 概述
- 一、基本思想
- 二、构造判别式:
- 三、递推出增量
- 优化:
- 总结:
- 四、例题分析
- 五、伪代码
概述
中点画线法(Midpoint Line Algorithm)是一种画线(Line Drawing)算法,用来在计算机屏幕上绘制线条。
它的基本思想是从线段的起点和终点出发,按照一定的规则向终点逐步逼近,并在途中以控制变量的方式得出每个像素点的坐标,从而绘制出所需的线条。
具体实现中,中点画线法通过计算线段斜率的变化情况,来分为斜率小于1和大于等于1两种情况,并采用Bresenham的对称性原理,以中点的颜色来控制每个像素点的生长方向,从而获得较高的绘制效率和图像质量表现。
总的来说,中点画线法是一种高效且易于实现的线段绘制算法,也是计算机图形学领域最基本的算法之一。
一、基本思想
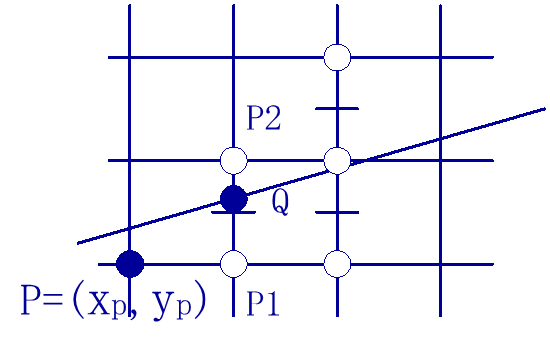
当前像素点为 ( x p , y p ) (x_p,y_p) (xp,yp),下一个像素点为 P 1 P1 P1或 P 2 P2 P2。
设 M = ( x p + 1 , y p + 0.5 ) M=(x_p+1,y_p+0.5) M=(xp+1,yp+0.5)为 P 1 P1 P1与 P 2 P2 P2之中点, Q Q Q为理想直线与 x = x p + 1 x=x_p+1 x=xp+1垂线的交点。将 Q Q Q与 M M M的 y y y坐标进行比较。
当 M M M在 Q Q Q的下方,则 P 2 P2 P2应为下一个像素点;当 M M M在 Q Q Q的上方,则 P 1 P1 P1应为下一个像素点。
二、构造判别式:
d = F ( M ) = F ( x p + 1 , y p + 0.5 ) = a ( x p + 1 ) + b ( y p + 0.5 ) + c d=F(M)=F(x_p+1,y_p+0.5)=a(x_p+1)+b(y_p+0.5)+c d=F(M)=F(xp+1,yp+0.5)=a(xp+1)+b(yp+0.5)+c
其中, a = y 0 − y 1 , b = x 1 − x 0 , c = x 0 y 1 − x 1 y 0 a=y_0-y_1, b=x_1-x_0, c=x_0y_1-x_1y_0 a=y0−y1,b=x1−x0,c=x0y1−x1y0.
- 当 d < 0 d<0 d<0时, M M M在 L ( Q L(Q L(Q点 ) ) )下方,取右上方 P 2 ( x p + 1 , y p + 1 ) P2(x_p+1,y_p+1) P2(xp+1,yp+1)为下一个像素;
- 当 d > 0 d>0 d>0时, M M M在 L ( Q L(Q L(Q点 ) ) )上方,取右方 P 1 ( x p + 1 , y p ) P1(x_p+1,y_p) P1(xp+1,yp)为下一个像素;
- 当 d = 0 d=0 d=0时,选 P 1 P1 P1或 P 2 P2 P2均可,约定取 P 1 ( x p + 1 , y p ) P1(x_p+1,y_p) P1(xp+1,yp)为下一个像素;

三、递推出增量
若当前像素处于:
d ≥ 0 d\geq 0 d≥0情况,则取正右方像素 P 1 ( x p + 1 , y p ) P1(x_p+1, y_p) P1(xp+1,yp),要判下一个像素位置,应计算
d 1 = F ( x p + 2 , y p + 0.5 ) = a ( x p + 2 ) + b ( y p + 0.5 ) = d + a d1=F(x_p+2, y_p+0.5)=a(x_p+2)+b(y_p+0.5)=d+a d1=F(xp+2,yp+0.5)=a(xp+2)+b(yp+0.5)=d+a
增量为 a a a。
d < 0 d<0 d<0时,则取右上方像素 P 2 ( x p + 1 , y p + 1 ) P2(x_p+1, y_p+1) P2(xp+1,yp+1)。要判断再下一像素,则要计算
d 2 = F ( x p + 2 , y p + 1.5 ) = a ( x p + 2 ) + b ( y p + 1.5 ) + c = d + a + b d2= F(x_p+2, y_p+1.5)=a(x_p+2)+b(y_p+1.5)+c=d+a+b d2=F(xp+2,yp+1.5)=a(xp+2)+b(yp+1.5)+c=d+a+b
增量为 a + b a+b a+b。
优化:
由于画线从 ( x 0 , y 0 (x_0, y_0 (x0,y0)开始, d d d的初值为:
d 0 = F ( x 0 + 1 , y 0 + 0.5 ) = F ( x 0 , y 0 ) + a + 0.5 b = a + 0.5 b d_0=F(x_0+1, y_0+0.5)=F(x_0, y_0)+a+0.5b=a+0.5b d0=F(x0+1,y0+0.5)=F(x0,y0)+a+0.5b=a+0.5b
可以用 2 d 2d 2d代替 d d d来避免小数,提高效率。令 d 0 = 2 a + b , d 1 = 2 a , d 2 = 2 a + 2 b d_0=2a+b, d_1=2a, d_2=2a+2b d0=2a+b,d1=2a,d2=2a+2b。
总结:
如果 d > 0 d > 0 d>0,则中点 ( x , y m ) (x_, y_m) (x,ym)在 L ( Q ) L(Q) L(Q)的上方,此时应该取右边的像素点 P 1 ( x p + 1 , y p ) P1(x_p+1,y_p) P1(xp+1,yp),即 x x x加1、 y y y不变。此时, d d d的值增加 d 1 d1 d1,即 d = d + d 1 d=d+d1 d=d+d1。
如果 d < 0 d<0 d<0,则中点 ( x m , y m ) (x_m, y_m) (xm,ym)在 L ( Q ) L(Q) L(Q)的下方,应该取右上方的像素点 P 2 ( x p + 1 , y p + 1 ) P2(x_p+1,y_p+1) P2(xp+1,yp+1),即 x x x和 y y y均加1。此时, d d d的值增加 d 2 d2 d2,即 d = d + d 2 d=d+d2 d=d+d2。
四、例题分析
以P0(0,0)到P1(5,2)为例,使用中点画线法,计算 d 0 d_0 d0, d 1 d_1 d1和 d 2 d_2 d2,并画出对应表格。
首先,根据两点坐标求出 a a a、 b b b、 c c c的值,有:
a = y 0 − y 1 = − 2 a=y_0-y_1=-2 a=y0−y1=−2
b = x 1 − x 0 = 5 b=x_1-x_0=5 b=x1−x0=5
c = x 0 y 1 − x 1 y 0 = − 10 c=x_0y_1-x_1y_0=-10 c=x0y1−x1y0=−10
接着,根据公式得到 d 0 d_0 d0, d 1 d_1 d1和 d 2 d_2 d2的初值,有:
d 0 = 2 a + b = 1 d_0 = 2a+b = 1 d0=2a+b=1
d 1 = 2 a = − 4 d_1 = 2a = -4 d1=2a=−4
d 2 = 2 a + 2 b = 6 d_2 = 2a+2b = 6 d2=2a+2b=6
然后,根据中点画线法的算法流程结合总结,可以按照如下表格计算每个像素点的坐标 ( x i , y i ) (x_i,y_i) (xi,yi)以及 d i d_i di的变化:
| count | x | y | d | P |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | P0 |
| 1 | 1 | 0 | -3 | |
| 2 | 2 | 1 | 3 | |
| 3 | 3 | 1 | -1 | |
| 4 | 4 | 2 | 5 | |
| 5 | 5 | 2 | 1 | P1 |
其中, P P P表示像素点位置, c o u n t count count表示计数, d d d表示中点到直线距离的判别式值(经过放大2倍),根据 d > 0 d>0 d>0还是 d < 0 d < 0 d<0判断所选的下一个像素点。对于 d = 0 d=0 d=0,约定选择右下方的像素点。
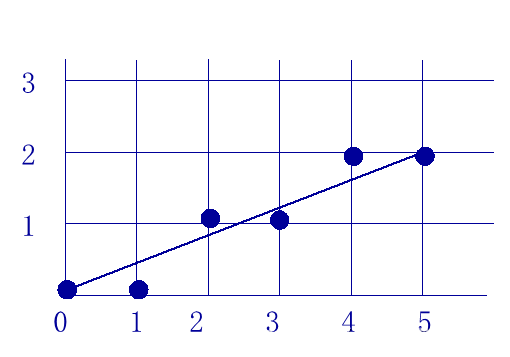
最终,依照算法,连线的轨迹如下:
P0 (0, 0) -> (1, 1) -> (2, 1) -> (3, 2) -> (4, 2) -> P1 (5, 2)
如下图:
五、伪代码
/* mid PointLine */
void Midpoint Line (int x0,int y0,int x1, int y1,int color){ int a, b, d1, d2, d, x, y;a=y0-y1, b=x1-x0, d=2*a+b;d1=2*a, d2=2* (a+b);x=x0, y=y0;drawpixel(x, y, color);while (x<x1){ if (d<0) {x++, y++, d+=d2; }else {x++, d+=d1;}drawpixel (x, y, color);} /* while */}
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!