[深度学习]吴恩达笔记——第二周
一、神经网络表示
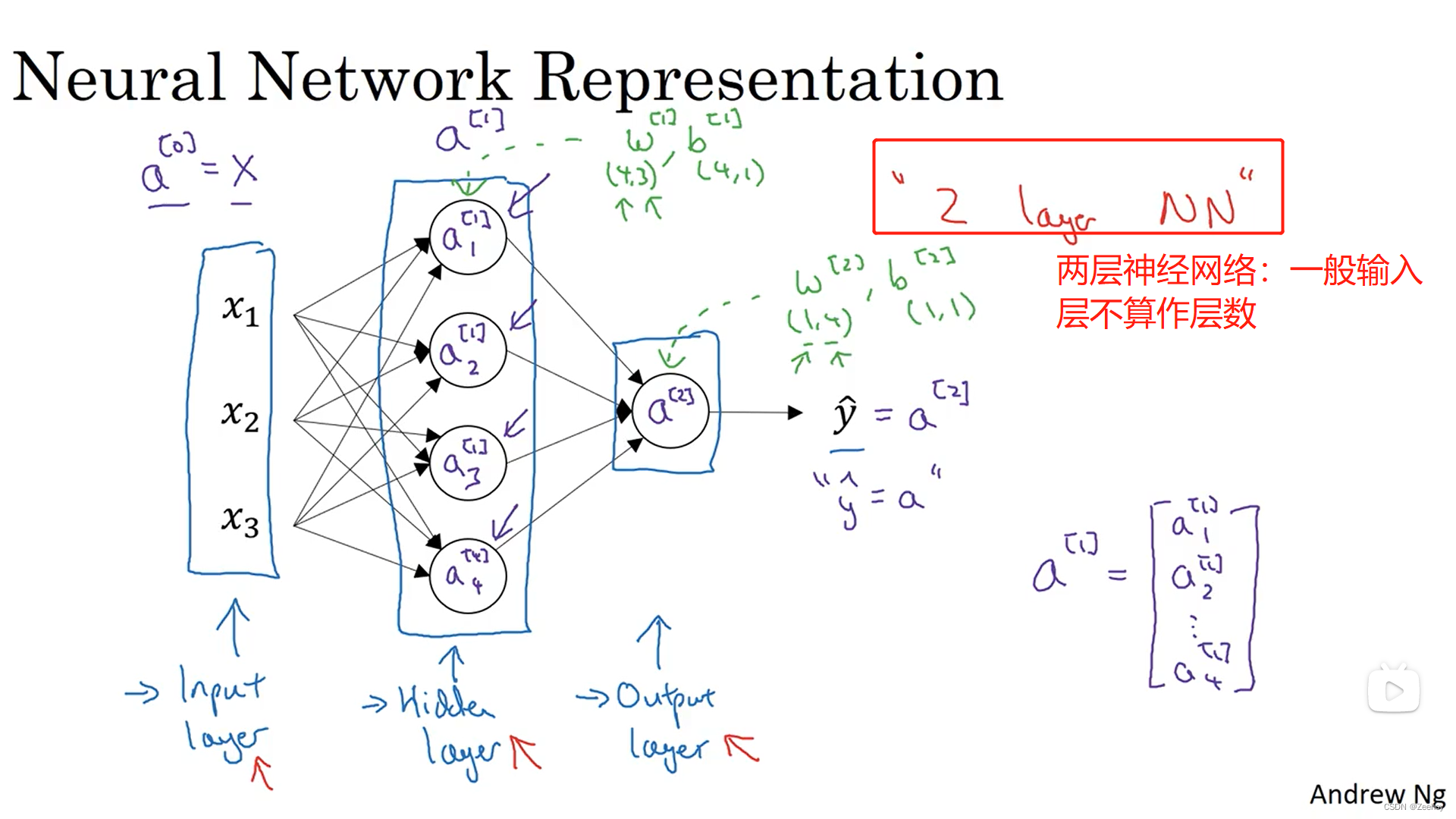
1. w [ 1 ] w^{[1]} w[1]是(4,3)的原因:第一层 a [ 1 ] a^{[1]} a[1]有4个节点,输入有3个特征
2. w [ 2 ] w^{[2]} w[2]是(1,4)的原因:输出层只有1个节点, a [ 1 ] a^{[1]} a[1]层有4个节点
二、神经网络的输出
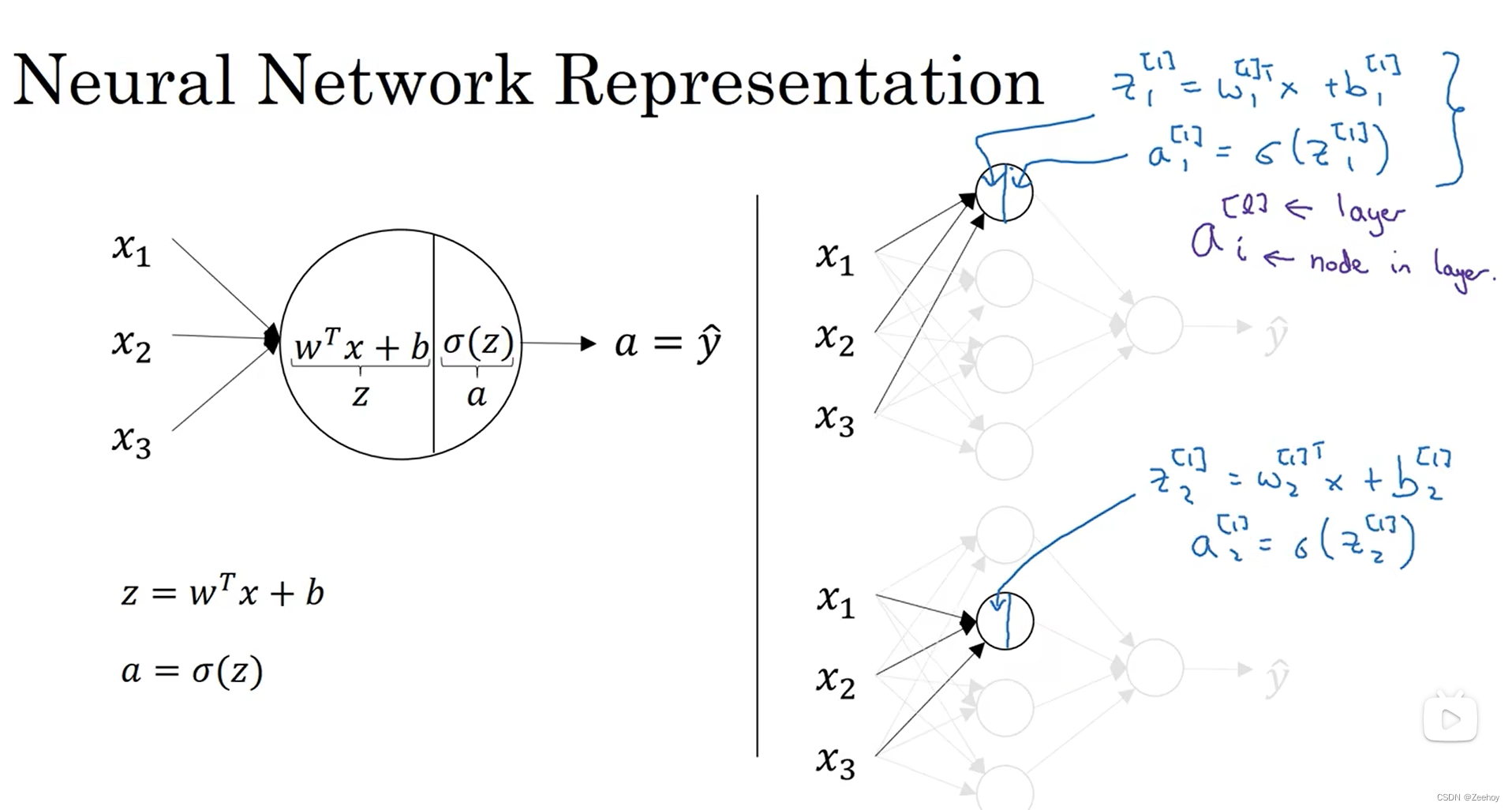
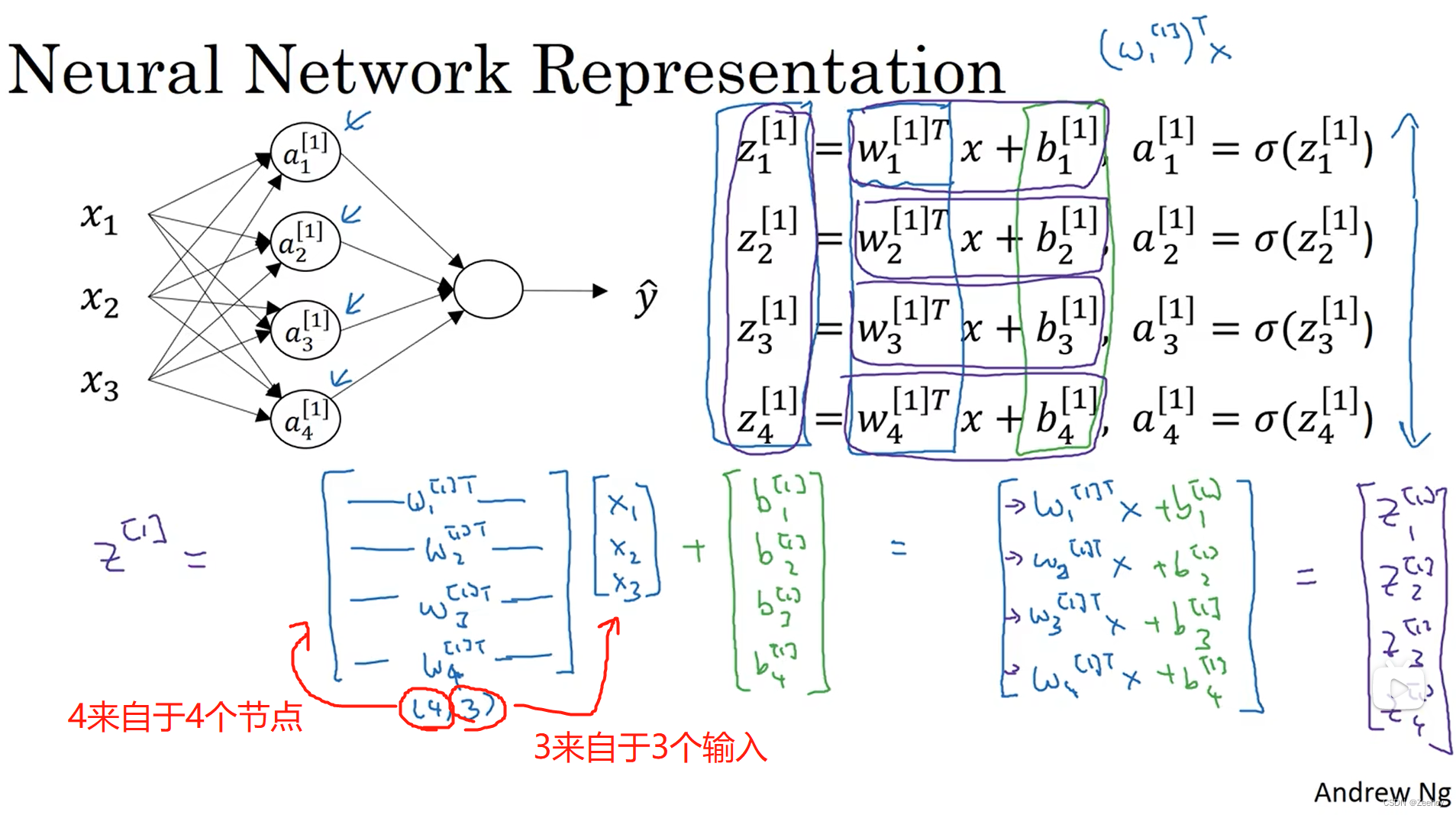
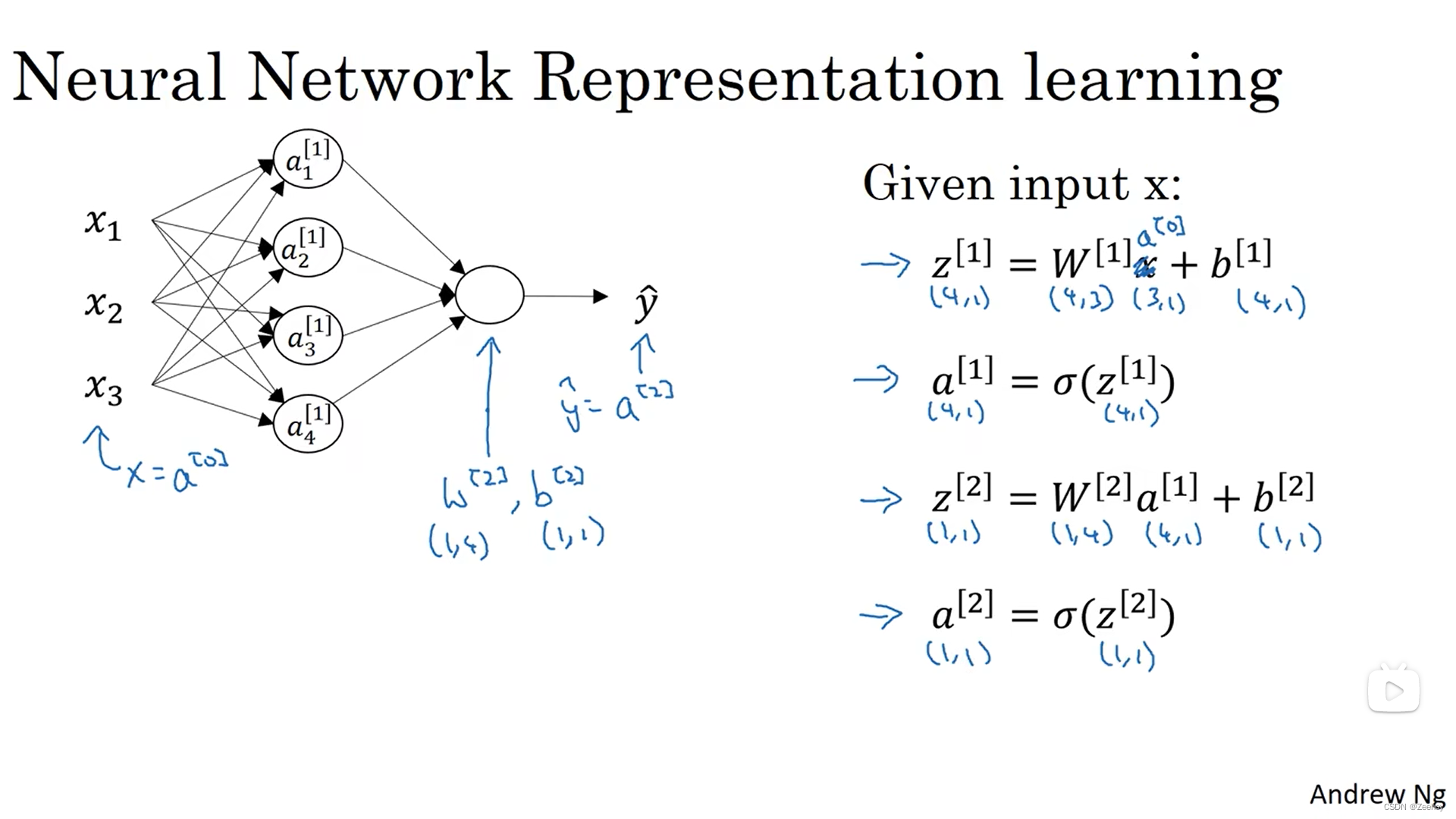
输入单个特征向量 x x x,得到神经网络的预测输出
三、多个样本的向量化


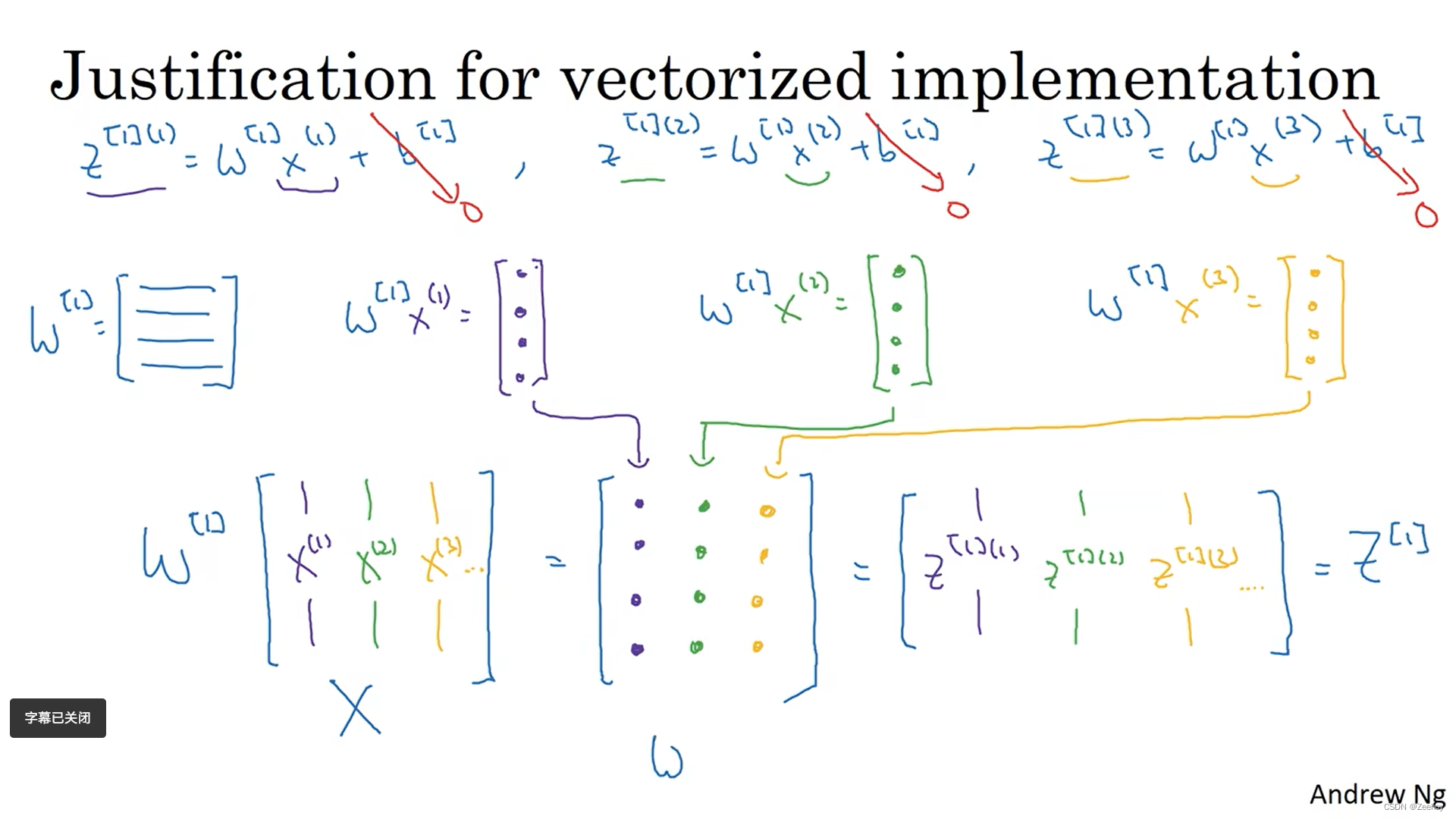
四、激活函数
1.sigmoid函数
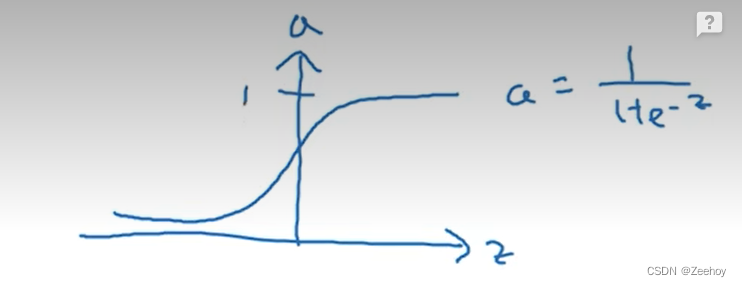
a = 1 1 + e − z a=\frac{1}{1+e^{-z}} a=1+e−z1
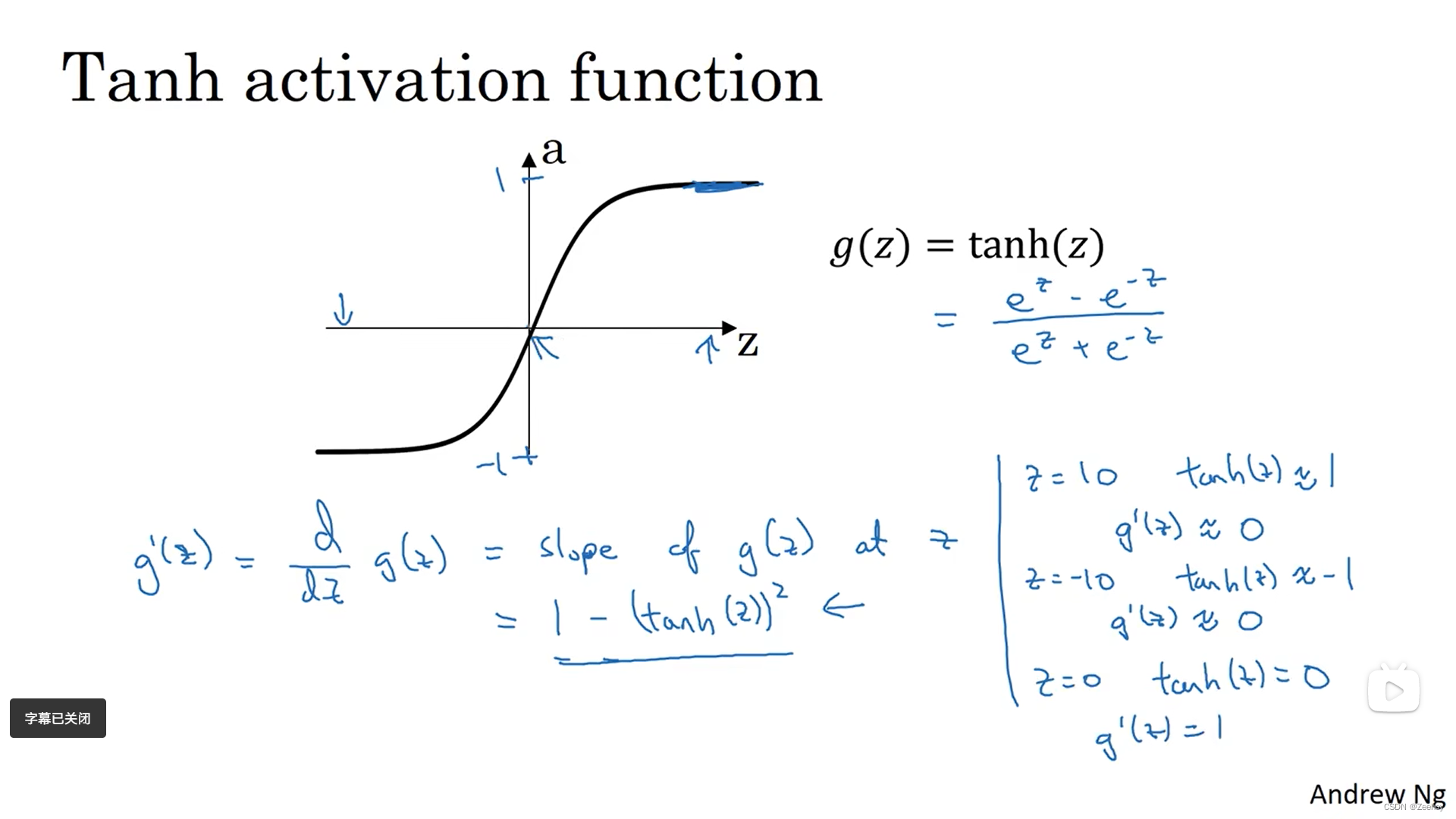
2.tanh函数(双曲正切函数)
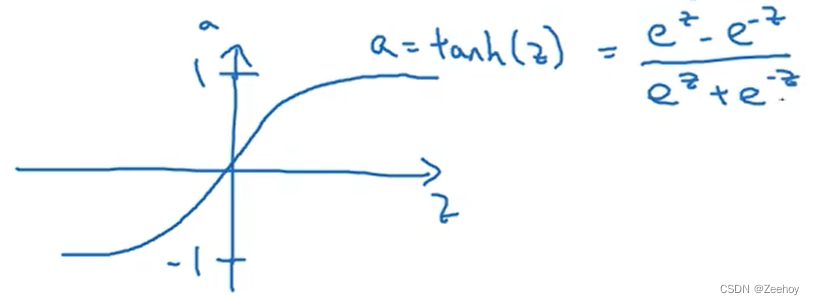
a = t a n h ( z ) = e z − e − z e z + e − z a=tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}} a=tanh(z)=ez+e−zez−e−z
对于隐藏层神经元来说,激活函数选用tanh函数的效果往往比sigmoid函数的效果要好,因为这使得函数的输出介于-1和1之间,导致输出的平均值更接近0。而在有些时候,是可能需要通过平移所有数据,使得数据的均值为0的。使用tanh函数同样导致了类似的数据中心化的效果,这使得下一层的学习更方便。
对于输出层神经元来说,激活函数选用sigmoid函数的效果更好,因为如果输出结果想要表示一个概率的大小,输出的值处于0到1之间显然更合理
sigmoid函数和tanh函数共有的缺点:
当输入值(z)非常大或非常小时,函数的梯度会变得非常小(梯度消失),会导致梯度下降算法的速度变慢。
3.ReLU函数(修正线性单元函数)
一个解决梯度消失问题的选择就是ReLU函数
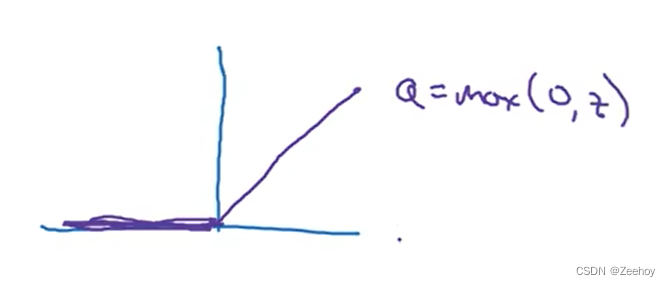
a = m a x ( 0 , z ) a=max(0,z) a=max(0,z)
只要输入值为正时,函数的导数永远都是1;当输入值为负时,函数的导数为0
当输入值为0时,函数的导数是没有定义的,但在实际编程中,z=0.00000000000…出现的概率是很低的。在实际中可以直接给z=0时的函数的导数赋值为1或者0。
现如今,ReLU函数已成为大多数情况下激活函数的默认选择,当不清楚隐藏层神经元该选用什么激活函数时,大多数人会选用ReLU函数
ReLU函数的缺点:
当输入值为负时,函数的导数全为0。但在实际中,有足够多的神经元的输入值是大于0,所以ReLU函数对于大多数训练样本来说,训练速度还是快的
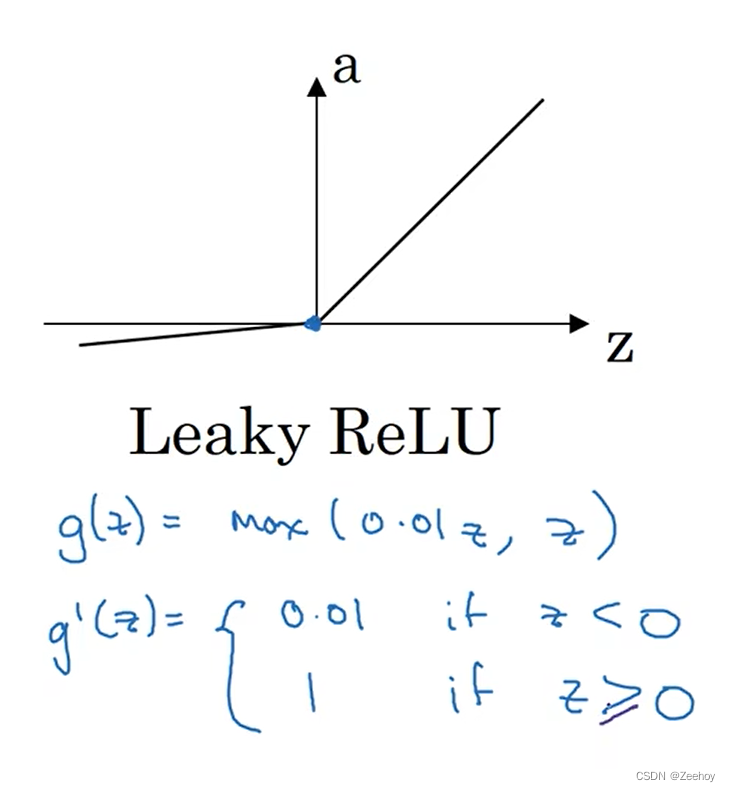
4.Leaky ReLU函数
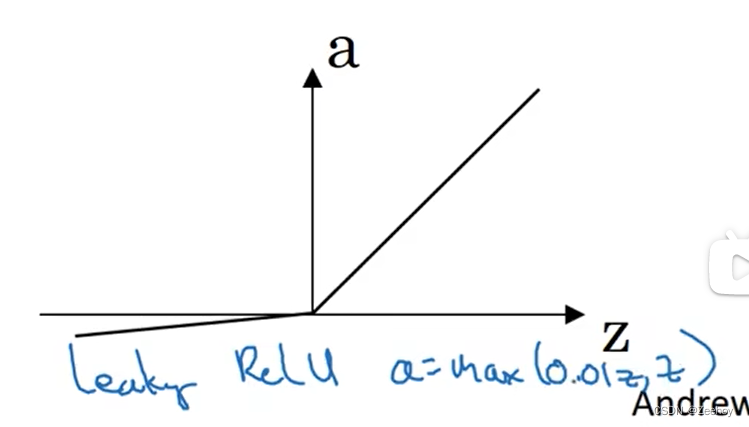
a = m a x ( 0.01 z , z ) a=max(0.01z,z) a=max(0.01z,z)
对于常数0.01来说,可以设成学习函数的另一个参数,通过训练得到最优值
五、激活函数为什么需要是非线性的?
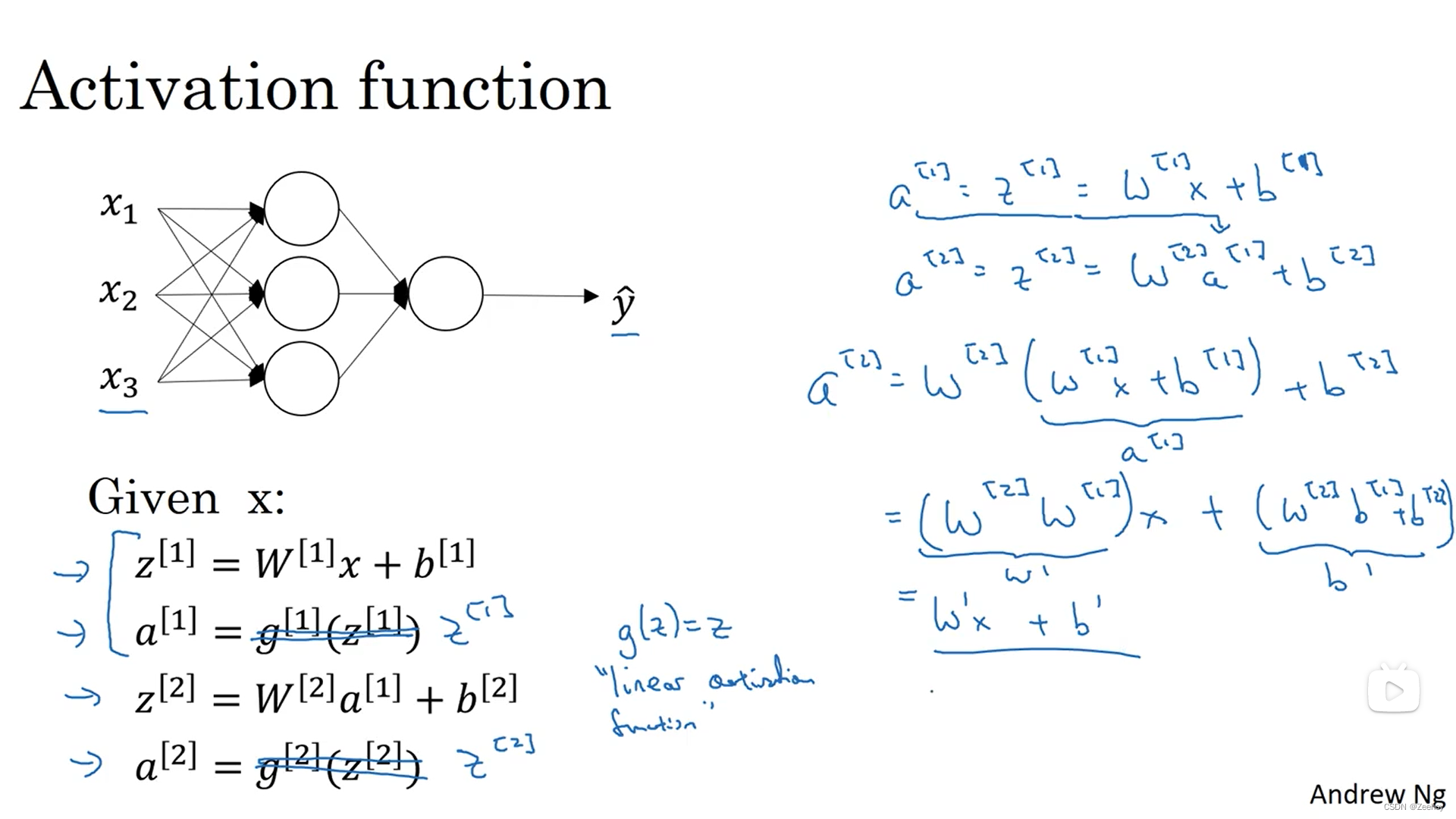
如果激活函数是线性的,那神经网络的输出就只是输入的线性组合,那么无论神经网络的隐藏层有多少层,都将变得没有意义。
只有一个情况下可以使用线性激活函数: a = z a=z a=z
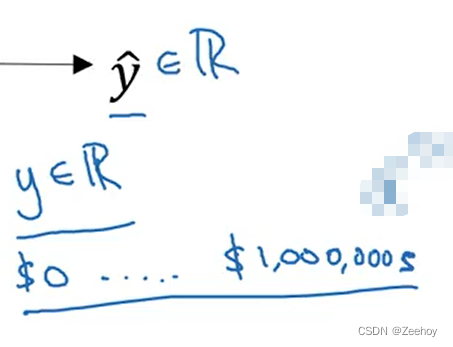
在回归问题中,预测的输出值是一个实数,比如说预测房地产价格,那么输出层神经元的激活函数或许可以选用线性激活函数
六、激活函数的导数
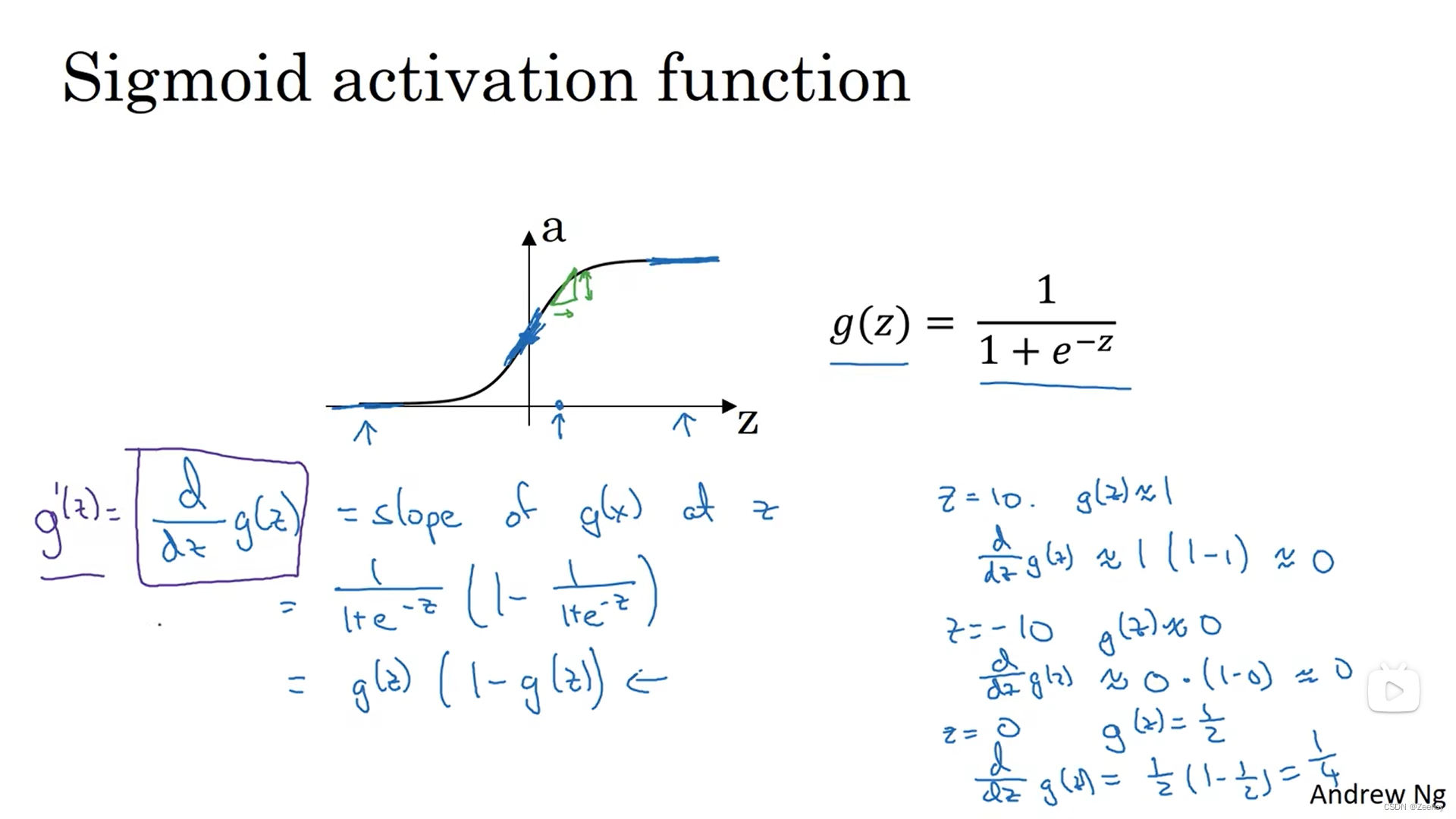
1.sigmoid函数
2.tanh函数
3.ReLU函数

4.Leaky ReLU
七、神经网络的梯度下降法

正向传播的公式:
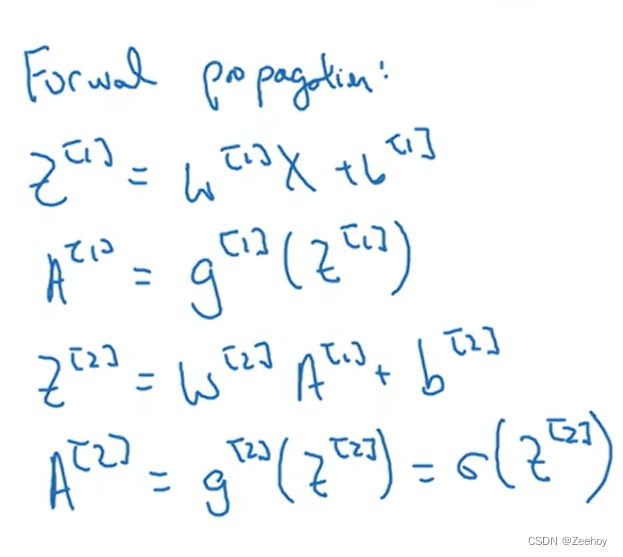
反向传播的公式:

keepdims=true用于防止python输出(n,)类型的数组,保证python输出的是矩阵。这个工作也可以通过reshape来实现。
八、反向传播公式的推导过程
1.Logistic回归

L ( a , y ) = − y l o g a − ( 1 − y ) l o g ( 1 − a ) L(a,y)=-yloga-(1-y)log(1-a) L(a,y)=−yloga−(1−y)log(1−a)
d a = d L d a = − y 1 a + ( 1 − y ) 1 1 − a = − y a + 1 − y 1 − a da=\frac{dL}{da}=-y\frac{1}{a}+(1-y)\frac{1}{1-a}=-\frac{y}{a}+\frac{1-y}{1-a} da=dadL=−ya1+(1−y)1−a1=−ay+1−a1−y
当激活函数选用sigmoid函数时:
a = s i g m o i d ( z ) = 1 1 + e − z a=sigmoid(z)=\frac{1}{1+e^{-z}} a=sigmoid(z)=1+e−z1
于是:
d a d z = − 1 ( 1 + e − z ) 2 ( 1 + e − z ) ′ = − 1 ( 1 + e − z ) 2 ( − e − z ) = e − z ( 1 + e − z ) 2 = 1 1 + e − z e − z 1 + e − z = 1 1 + e − z 1 + e − z − 1 1 + e − z = 1 1 + e − z ( 1 − 1 1 + e − z ) = a ( 1 − a ) \frac{da}{dz}=-\frac{1}{(1+e^{-z})^2}(1+e^{-z})' \\ \\=-\frac{1}{(1+e^{-z})^2}(-e^{-z}) \\ \\=\frac{e^{-z}}{(1+e^{-z})^2} \\ \\=\frac{1}{1+e^{-z}}\frac{e^{-z}}{1+e^{-z}} \\ =\frac{1}{1+e^{-z}}\frac{1+e^{-z}-1}{1+e^{-z}} \\ =\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}}) \\ =a(1-a) dzda=−(1+e−z)21(1+e−z)′=−(1+e−z)21(−e−z)=(1+e−z)2e−z=1+e−z11+e−ze−z=1+e−z11+e−z1+e−z−1=1+e−z1(1−1+e−z1)=a(1−a)
d z = d L d z = d L d a d a d z = ( − y a + 1 − y 1 − a ) [ a ( 1 − a ) ] = a − y dz=\frac{dL}{dz}=\frac{dL}{da}\frac{da}{dz}=(-\frac{y}{a}+\frac{1-y}{1-a})[a(1-a)]=a-y dz=dzdL=dadLdzda=(−ay+1−a1−y)[a(1−a)]=a−y
d w = d L d a d a d z d z d w = ( a − y ) x = d z ⋅ x dw=\frac{dL}{da}\frac{da}{dz}\frac{dz}{dw}=(a-y)x=dz·x dw=dadLdzdadwdz=(a−y)x=dz⋅x
d b = d L d a d a d z d z d b = ( a − y ) = d z db=\frac{dL}{da}\frac{da}{dz}\frac{dz}{db}=(a-y)=dz db=dadLdzdadbdz=(a−y)=dz
2.双层神经网络
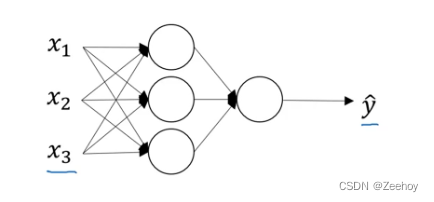
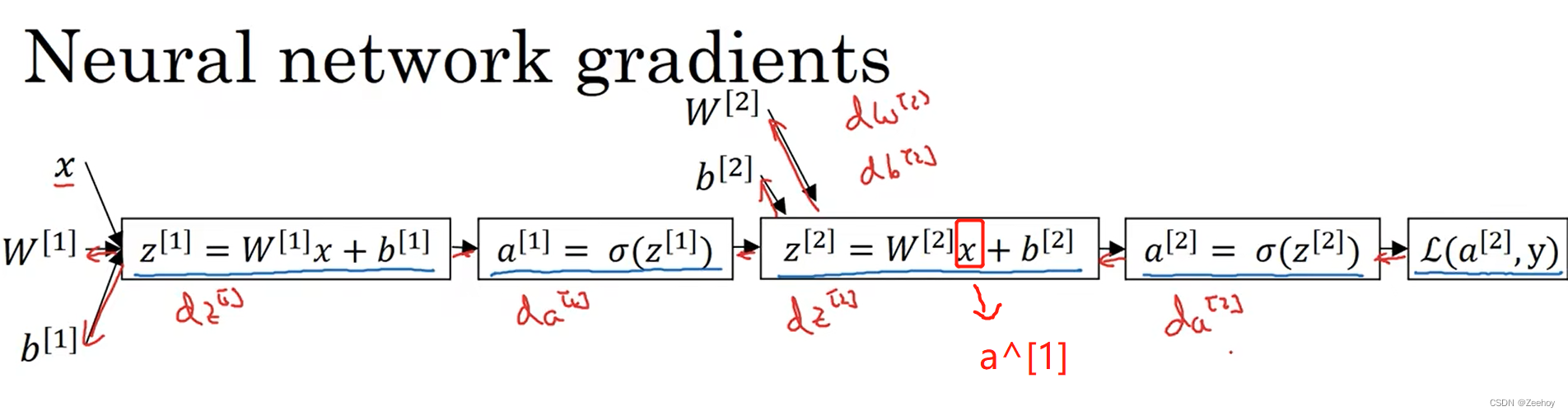
最后一层输出层的激活函数是sigmoid函数,与Logistics回归类似,因此反向传播也与Logistics回归类似,请注意,最后一层输出层的输入 x x x 实际上是前一层的输出 a [ 1 ] a^{[1]} a[1] :
d z [ 2 ] = a [ 2 ] − y dz^{[2]}=a^{[2]}-y dz[2]=a[2]−y
d W [ 2 ] = d z [ 2 ] ⋅ a [ 1 ] T dW^{[2]}=dz^{[2]}·a^{[1]^T} dW[2]=dz[2]⋅a[1]T
d b [ 2 ] = d z [ 2 ] db^{[2]}=dz^{[2]} db[2]=dz[2]
而前一层的导数根据链式法则进行求解:
d z [ 1 ] = d L d a [ 2 ] d a [ 2 ] d z [ 2 ] d z [ 2 ] d a [ 1 ] d a [ 1 ] d z [ 1 ] dz^{[1]}=\frac{dL}{da^{[2]}}\frac{da^{[2]}}{dz^{[2]}}\frac{dz^{[2]}}{da^{[1]}}\frac{da^{[1]}}{dz^{[1]}} dz[1]=da[2]dLdz[2]da[2]da[1]dz[2]dz[1]da[1]
= d z [ 2 ] ⋅ d z [ 2 ] d a [ 1 ] ⋅ d a [ 1 ] d z [ 1 ] =dz^{[2]}·\frac{dz^{[2]}}{da^{[1]}}·\frac{da^{[1]}}{dz^{[1]}} =dz[2]⋅da[1]dz[2]⋅dz[1]da[1]
= W [ 2 ] T d z [ 2 ] ∗ g [ 1 ] ′ ( z [ 1 ] ) , ∗ 意味着矩阵逐元素相乘得到新的矩阵 =W^{[2]^T}dz^{[2]}*g^{[1]'}(z^{[1]}),*意味着矩阵逐元素相乘得到新的矩阵 =W[2]Tdz[2]∗g[1]′(z[1]),∗意味着矩阵逐元素相乘得到新的矩阵
d W [ 1 ] = d z [ 1 ] ⋅ x T dW^{[1]}=dz^{[1]}·x^T dW[1]=dz[1]⋅xT
d b [ 1 ] = d z [ 1 ] db^{[1]}=dz^{[1]} db[1]=dz[1]
需要注意各矩阵间的维度关系
九、L2正则化
正则化是为了防止神经网络过拟合

λ 2 m ∑ l = 1 L ∣ ∣ w [ l ] ∣ ∣ F 2 = λ 2 m ( ∣ ∣ w [ 1 ] ∣ ∣ F 2 + ∣ ∣ w [ 2 ] ∣ ∣ F 2 + . . . + ∣ ∣ w [ L ] ∣ ∣ F 2 ) \frac{\lambda}{2m}\sum_{l=1}^{L}||w^{[l]}||_F^2=\frac{\lambda}{2m}(||w^{[1]}||_F^2+||w^{[2]}||_F^2+...+||w^{[L]}||_F^2) 2mλl=1∑L∣∣w[l]∣∣F2=2mλ(∣∣w[1]∣∣F2+∣∣w[2]∣∣F2+...+∣∣w[L]∣∣F2)
这块东西对 w [ 1 ] w^{[1]} w[1] 求导,除 w [ 1 ] w^{[1]} w[1] 外全为0了:
∂ λ 2 m ∣ ∣ w [ 1 ] ∣ ∣ F 2 ∂ w [ 1 ] = λ 2 m ∂ w [ 1 ] T w [ 1 ] ∂ w [ 1 ] = λ 2 m 2 w [ 1 ] = λ m w [ 1 ] \frac{\partial \frac{\lambda}{2m}||w^{[1]}||_F^2}{\partial w^{[1]}}=\frac{\lambda}{2m}\frac{\partial w^{[1]^{T}}w^{[1]}}{\partial w^{[1]}}=\frac{\lambda}{2m}2w^{[1]}=\frac{\lambda}{m}w^{[1]} ∂w[1]∂2mλ∣∣w[1]∣∣F2=2mλ∂w[1]∂w[1]Tw[1]=2mλ2w[1]=mλw[1]
参考矩阵求导:
∂ x T x ∂ x = 2 x \frac{\partial x^Tx}{\partial x}=2x ∂x∂xTx=2x

从直觉上来看,正则化参数 λ \lambda λ 使得权重矩阵 w [ l ] w^{[l]} w[l] 被设置为接近0的值,基本上使得某些隐藏层的神经元的影响降低,从而将这个大规模的过拟合的神经网络简化成了深度大但每层神经元数量小的网络,使得其偏向于高偏差状态,但 λ \lambda λ 还可以取到中间值,使这个网络达到中间刚好的状态。
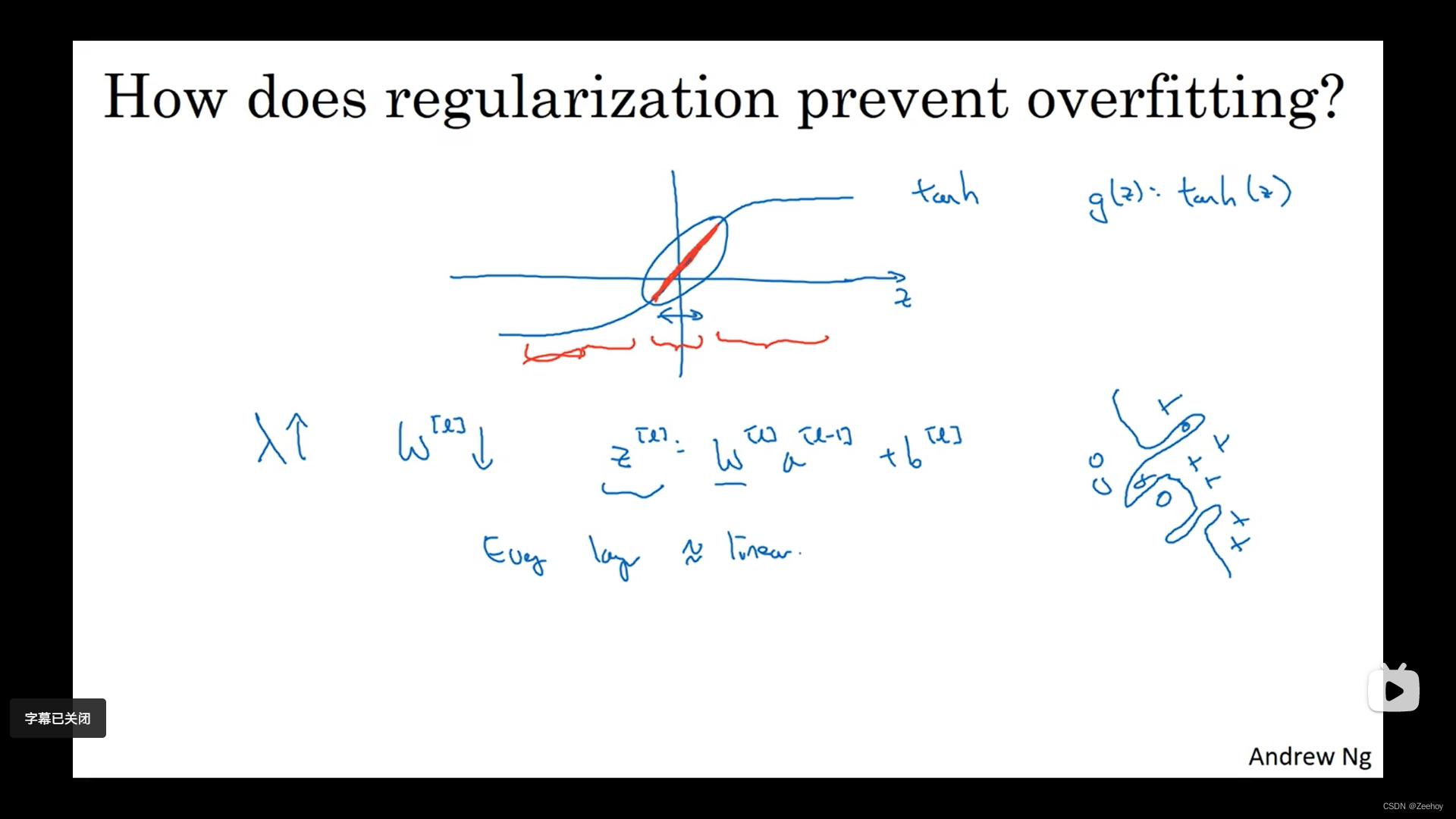
z z z 相对变小, 使得激活函数会相对呈现更接近线性的性质,使整个神经网络会更接近线性函数而不是一个极度复杂的非线性函数,因此不会发生过拟合。
十、dropout正则化

a [ 3 ] a^{[3]} a[3] 再除以 keep-prob 的原因: a [ 3 ] a^{[3]} a[3] 中有20%的元素被归零了,为了不影响 z [ 4 ] z^{[4]} z[4] 的期望值
dropout的缺点:成本函数 J J J 不再被明确定义,不再能通过 p l o t plot plot 成本函数 J J J 的数值变化曲线来观察每次迭代后成本函数是否有在下降。
解决方法:先关闭dropout,运行代码,plot成本函数,确保它在每次迭代都单调递减。再加入dropout。
十一、成本函数优化算法
1.batch梯度下降法
2.随机梯度下降法
永远不会收敛,会一直在最小值附近波动
3.mini-batch梯度下降法

4.动量梯度下降法(Momentum)

V d w = β V d w + ( 1 − β ) d w V_{dw}=\beta V_{dw}+(1-\beta)dw Vdw=βVdw+(1−β)dw
V d b = β V d b + ( 1 − β ) d b V_{db}=\beta V_{db}+(1-\beta)db Vdb=βVdb+(1−β)db
W : = W − α V d w W:=W-\alpha V_{dw} W:=W−αVdw
b : = b − α V d b b:=b-\alpha V_{db} b:=b−αVdb
4.RMSprop(root,mean,square)
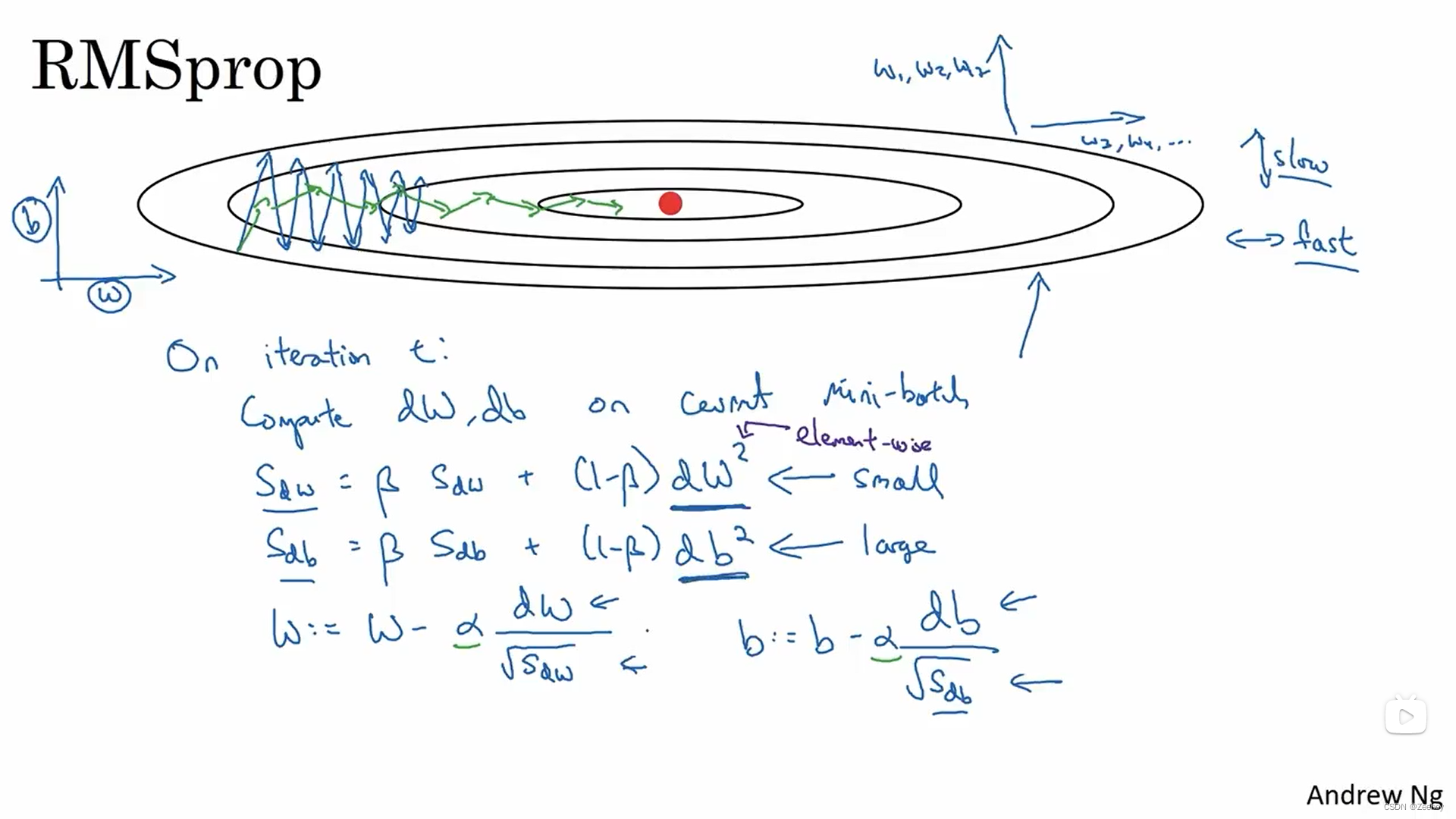
S d w = β S d w + ( 1 − β ) ( d w ) 2 S_{dw}=\beta S_{dw}+(1-\beta)(dw)^2 Sdw=βSdw+(1−β)(dw)2
S d b = β S d b + ( 1 − β ) ( d b ) 2 S_{db}=\beta S_{db}+(1-\beta)(db)^2 Sdb=βSdb+(1−β)(db)2
W : = W − α d w S d w W:=W-\alpha \frac{dw}{\sqrt{S_{dw}}} W:=W−αSdwdw
b : = b − α d b S d b b:=b-\alpha \frac{db}{\sqrt{S_{db}}} b:=b−αSdbdb
5.Adam(Adapt moment estimation)
RMSprop和Adam优化算法是少有的被证明适用于不同的深度学习结构的算法
Adam算法实际上是将Momentum算法和RMSprop算法结合在一起

Momentum部分:
V d w = β 1 V d w + ( 1 − β 1 ) d w V_{dw}=\beta_1 V_{dw}+(1-\beta_1)dw Vdw=β1Vdw+(1−β1)dw
V d b = β 1 V d b + ( 1 − β 1 ) d b V_{db}=\beta_1 V_{db}+(1-\beta_1)db Vdb=β1Vdb+(1−β1)db
RMSprop部分:
S d w = β 2 S d w + ( 1 − β 2 ) ( d w ) 2 S_{dw}=\beta_2 S_{dw}+(1-\beta_2)(dw)^2 Sdw=β2Sdw+(1−β2)(dw)2
S d b = β 2 S d b + ( 1 − β 2 ) ( d b ) 2 S_{db}=\beta_2 S_{db}+(1-\beta_2)(db)^2 Sdb=β2Sdb+(1−β2)(db)2
偏差修正:
V d w c o r r e c t e d = V d w 1 − β 1 t V_{dw}^{corrected}=\frac{V_{dw}}{1-\beta_1^t} Vdwcorrected=1−β1tVdw
V d b c o r r e c t e d = V d b 1 − β 1 t V_{db}^{corrected}=\frac{V_{db}}{1-\beta_1^t} Vdbcorrected=1−β1tVdb
S d w c o r r e c t e d = S d w 1 − β 2 t S_{dw}^{corrected}=\frac{S_{dw}}{1-\beta_2^t} Sdwcorrected=1−β2tSdw
S d b c o r r e c t e d = S d b 1 − β 2 t S_{db}^{corrected}=\frac{S_{db}}{1-\beta_2^t} Sdbcorrected=1−β2tSdb
权重更新:
W : = W − α V d w c o r r e c t e d S d w c o r r e c t e d + ϵ W:=W-\alpha \frac{V_{dw}^{corrected}}{\sqrt{S_{dw}^{corrected}}+\epsilon} W:=W−αSdwcorrected+ϵVdwcorrected
b : = b − α V d b c o r r e c t e d S d b c o r r e c t e d + ϵ b:=b-\alpha \frac{V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+\epsilon} b:=b−αSdbcorrected+ϵVdbcorrected
超参数:

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!