数据结构实验报告

1. 问题描述及分析

问题描述：实现一元多项式的加法.

要求：（1）编程实现一元多项式的加法。

1. 编写一个测试主函数

分析：对于任意一元多项式

      Pn(x)=p0+p1X^1+p2X^2+...+piXi+...+pnXn

可以抽象一个为一个由“系数——指数”对构成的线性表，且线性表中各元素的指数项式递增的、p=((p0,0），（p1,1),(p2,2),...,(pn,n))

用一个单链表表示上述线性表，其结点结构为：

typedef  struct node{float  coef;//系数域int exp;//指针域struct node *next;//指针域}PloyNode;

(1)建立单链表功能

建立一个顺序表，确定DataType与Node。

（2）初始化

将单链表初始化。

（3）插入功能

输入的形式：在带头节点的单链表head的第i个（0~size）个结点前插入一个存放元素x的结点，首先要在单链表中找到ai-1结点并由指针p指示，然后动态申请一个内存单元并由指针q指示，并把元素x的值赋予新的结点的数据域（即q->data=x),最后修改新的结点的指针指向ai的结点（q->next=p->next),并修改ai-1结点的指针域使之指向新结点q（即p->next=q).

输出的形式：如果输入的参数不合法，则显示参数错误信息。

返回值：插入成功返回1，插入失败返回0。

（4）删除功能

输入的形式：要在带头结点的单链表中删除ai结点，首先要在单链表中寻找到ai-1结点并由指针p指示，然后让指针s指向ai结点（s=p->next),并把ai结点数据域赋予元素x（*x=s->data),最后把ai结点脱链（p->next=p->next->next),并动态释放ai结点的内存单元（free（s）).

输出的形式：如果输入的参数不合法或顺序表为空，则显示参数错误信息。

返回值：删除成功返回1，删除失败返回0。

（5）查找功能

输入的形式与输入值的范围：输入一个表示查找位置且小于MaxSize的非负整数。

输出的形式：如果输入的参数不合法，则显示参数错误信息。

返回值：查找成功返回1，查找失败返回0。

1. 概要设计

1.打算采用书中的链式存储来储存多项式的各项系数和指数。使用的数据结构也和书上的一致，包含该项的系数，指数以及指向下一项的指针。

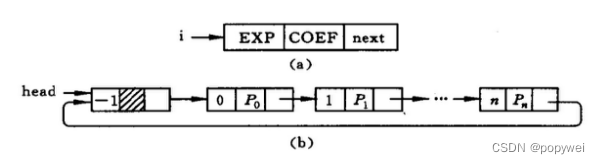
2.数据结构：

typedef struct node{int exp;                //指数float coef;             //系数struct NODE* next;    //指针域}PloyNode;

3.算法描述：

  用带有头结点的线性链表表示多项式A（x），B（x），设指针hA，hB，hC分别为指向多项式链表A（x），B（x）的头指针，指针p,q的初始位置分别指向A（x），B（x）中第一项，则求A（x）+B（x）的运算过程为：比较p,q所指结点中的指数项，若EXP（p）EXP（q），则把q节点存储的的系数和指数传给C（x）新创建的一个节点，q指向下一个节点，p不动；若EXP（p）=EXP（q），则将两个结点中的系数相加，当和不为零时把这个和以及系数传给C（x）新创建的一个节点。如果有一个多项式的所有项都已经处理过，只需要把没处理完的多项式剩下的项全部加到C（x）即可。

（4）①在开始设计时，考虑到功能分块，所以写了以下几个函数：

   Link Create(int num)    //用于创建多项式

   Link AddPoly(Link heada, Link headb)      //多项式运算

   void printpoly(Link head)    //打印（输出）

1. 详细设计

//一元多项式相加#include #include typedef struct node{int exp;                //指数float coef;             //系数struct NODE* next;    //指针域}PloyNode;Link Create(int num)        //建立一个多项式（利用尾插法）{printf("\n"); //换行int tempexp = 0;        //临时指数float tempcoef = 0;     //临时系数Link head = (Link)malloc(sizeof(Node));head->next = NULL;Link rear = head;rear->next = NULL;//输入部分链接链表结点for (int i = 1; i <= num; i++){printf("请输入第%d项的次数和系数：", i);scanf("%d %f", &tempexp, &tempcoef);    //输入Link temp = (Link)malloc(sizeof(Node));temp->exp = tempexp;temp->coef = tempcoef;rear->next = temp;rear = temp;}rear->next = NULL;return head;                  //返回头结点}void printpoly(Link head)        //打印多项式{Link p = head->next;while (p != NULL){if(p->coef>0)  //如果系数是负数则加个括号printf("%.1fX^%d", p->coef, p->exp);elseprintf("(%.1f)X^%d", p->coef, p->exp);if (p->next != NULL)printf("+");         //加号的打印p = p->next;}}Link AddPoly(Link heada, Link headb)      //进行多项式相加{Link headc = (Link)malloc(sizeof(Node));headc->next = NULL;Link rear = headc;Link pa = heada->next;Link pb = headb->next;Link pc = headc->next;while (pa != NULL || pb != NULL)    //如果都为空就结束{Link temp = (Link)malloc(sizeof(Node));temp->next = NULL;if (pa != NULL && pb != NULL)    //如果都不为空就可以找到合适的项相加{if ((pa->exp) < (pb->exp) )    //b的这一项指数大{temp->exp = pa->exp;temp->coef = pa->coef;rear->next = temp;rear = temp;pa = pa->next;}else if ((pa->exp) == (pb->exp))    //指数相同{if (pa->coef + pb->coef == 0)   //系数如果加起来等于0{pa = pa->next;pb = pb->next;}else                            //系数加起来不为0{temp->exp = pa->exp;temp->coef = pa->coef + pb->coef;rear->next = temp;rear = temp;pa = pa->next;pb = pb->next;}}else if ((pa->exp) > (pb->exp) )     //a的这一项指数大{temp->exp = pb->exp;temp->coef = pb->coef;rear->next = temp;rear = temp;pb = pb->next;}}else if (pa != NULL && pb == NULL)//b多项式所有项处理完了，a还没处理完{temp->exp = pa->exp;temp->coef = pa->coef;rear->next = temp;rear = temp;pa = pa->next;}else if (pa == NULL && pb != NULL)//a多项式所有项处理完了，b还没处理完{temp->exp = pb->exp;temp->coef = pb->coef;rear->next = temp;rear = temp;pb = pb->next;}}return headc;}int main(){int n1 = 0, n2 = 0;Link hc = NULL;//创立多项式Aprintf("\n构建多项式A\n");printf("请输入多项式的项数：");scanf("%d", &n1);Link ha = Create(n1);printf("多项式A:");printpoly(ha);printf("\n");//创立多项式Bprintf("\n构建多项式B\n");printf("请输入多项式的项数：");scanf("%d", &n2);Link hb = Create(n2);printf("多项式B:");printpoly(hb);printf("\n");//计算出多项式Chc=AddPoly(ha, hb);printf("\nRESULT:\n多项式C:");printpoly(hc);return 0;}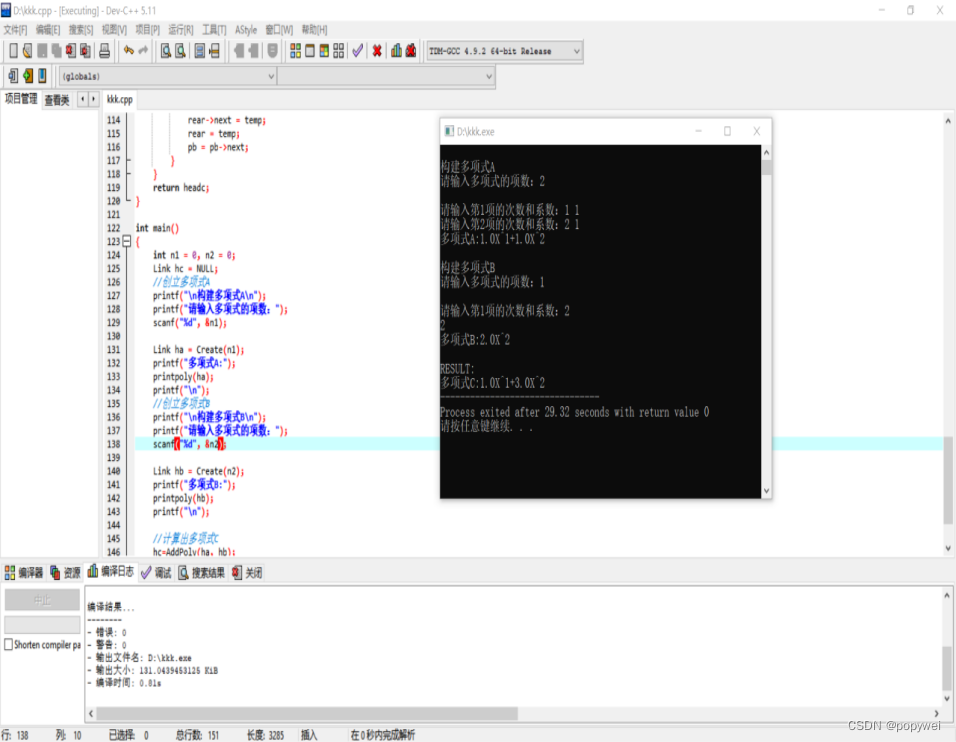

调试与分析

该结果与预期结果一致

1. 总结

1.一元多项式的加法，我是考虑特殊化的，默认是从小到大排序的

2.在写算法的时候没有考虑到可能多项式系数经过运算可能为负数，所以在测试时，原先如果有某一项相加结果是负数，则会出现“+-”这样的情况。所以在程序中加入判断：

if(p->coef>0)  //如果系数是负数则加个括号

printf("%.1fX^%d", p->coef, p->exp);

else

printf("(%.1f)X^%d", p->coef, p->exp);解决了问题。

3.输出时用了%.1f,控制宽度，使输出更好看

4.算法思想太特殊化了，还需改善。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！