概率论与数理统计期末复习
文章目录
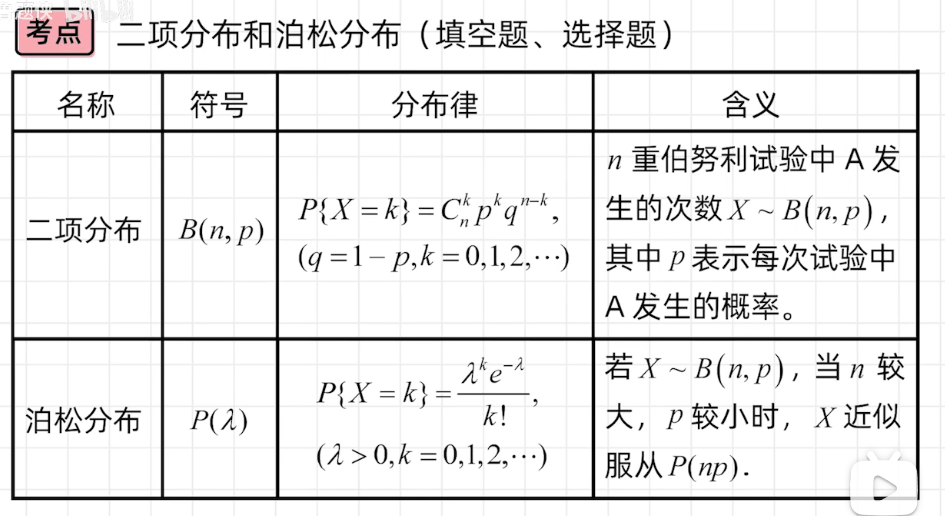
- 泊松分布
- 连续性随机变量概率密度
- 均匀分布
- 离散型随机变量函数的分布
- 二维离散型随机变量的分布
- 二维随机变量的的分布
- 离散型随机变量函数的分布
- 连续性随机变量函数的分布
- 正太分布可加性
- 数学期望
- 方差和标准差
- 常见的随机变量的期望和方差
- 协方差和相关系数
- 二维离散型随机变量期望与方差的计算
- 中心极限定理
- 三大分布
- 矩估计
- 极大似然估计
- 假设检验
- 假设检验

泊松分布

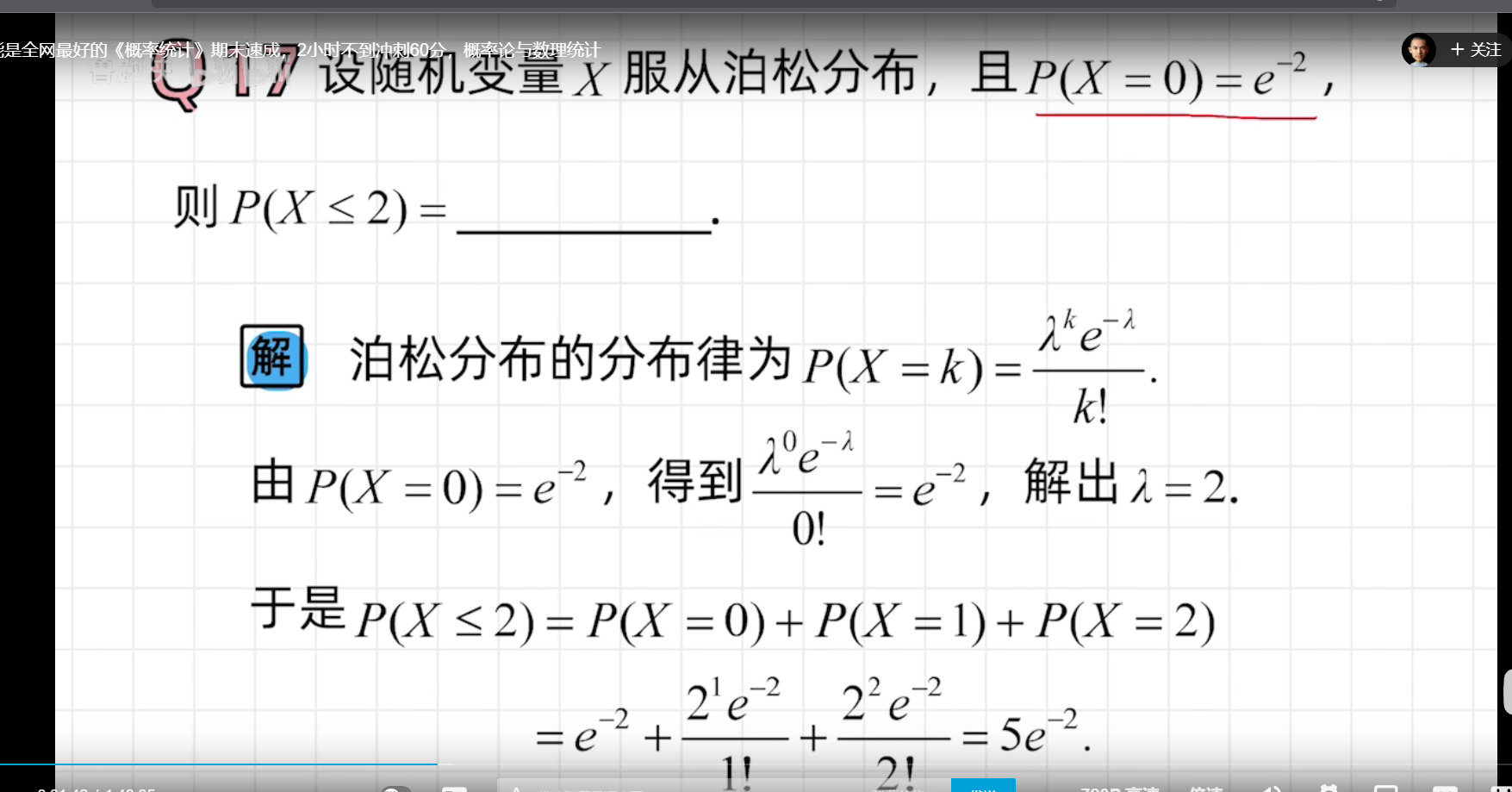
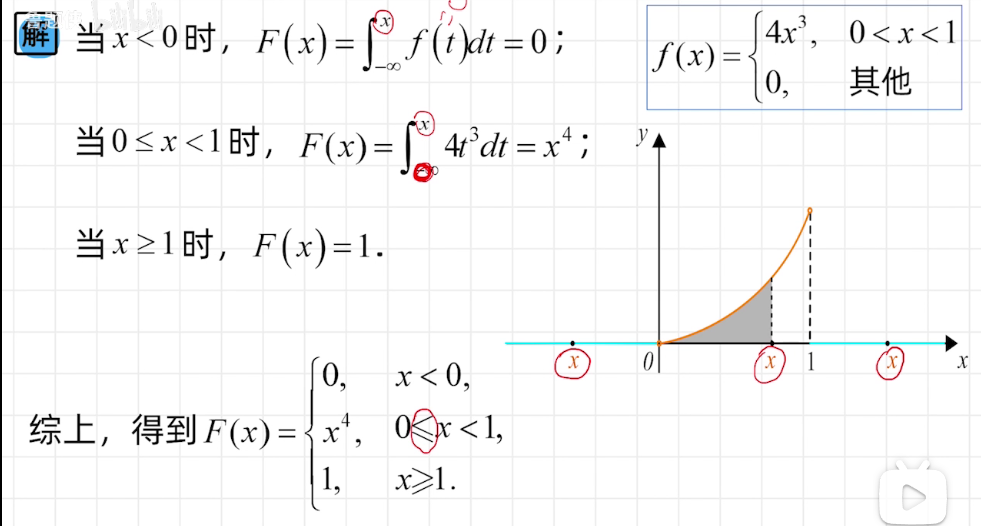
连续性随机变量概率密度
概率密度积分求分布函数,概率密度函数积分求概率,分布函数端点值相减为概率


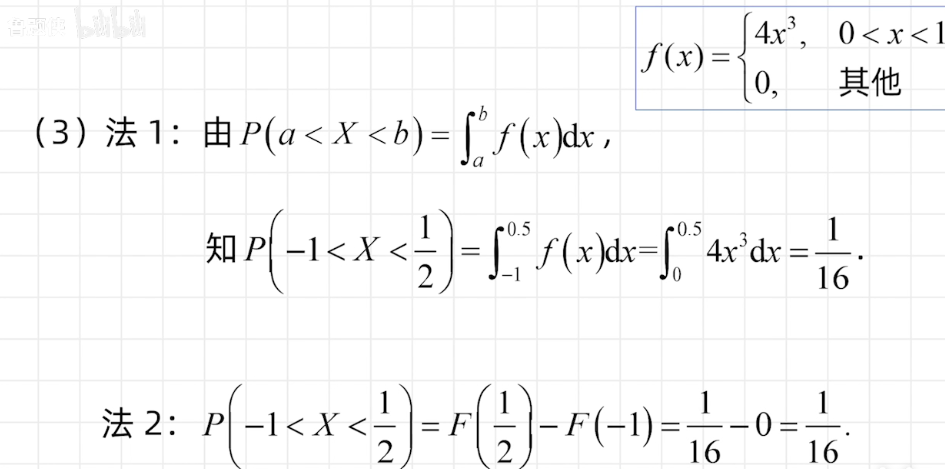


均匀分布


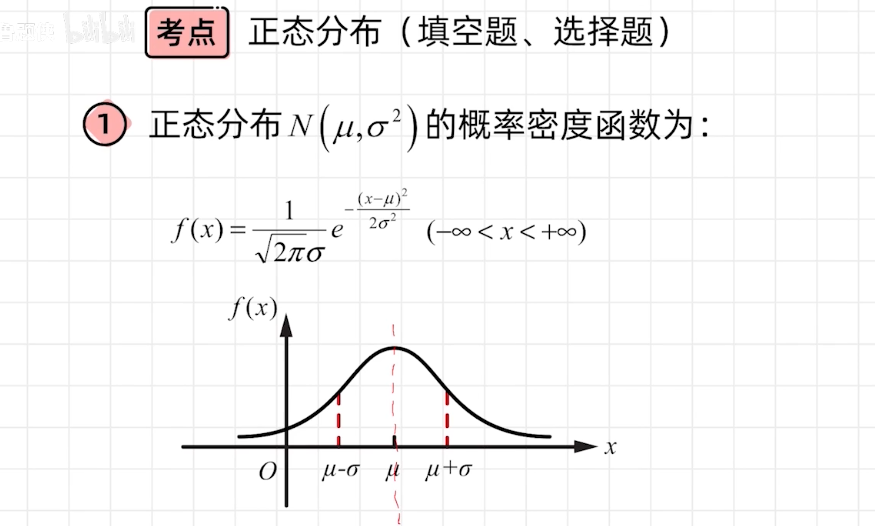
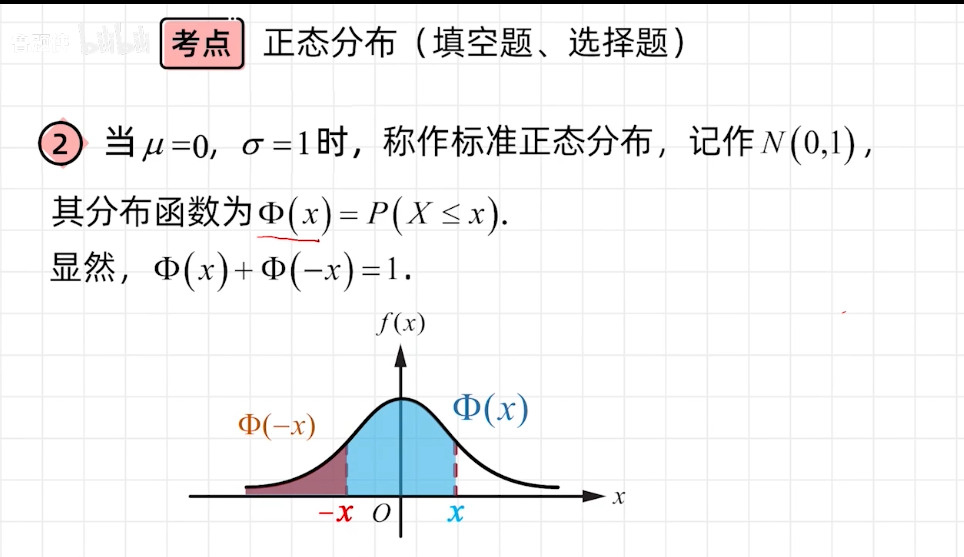
正太分布标准化

例题

离散型随机变量函数的分布
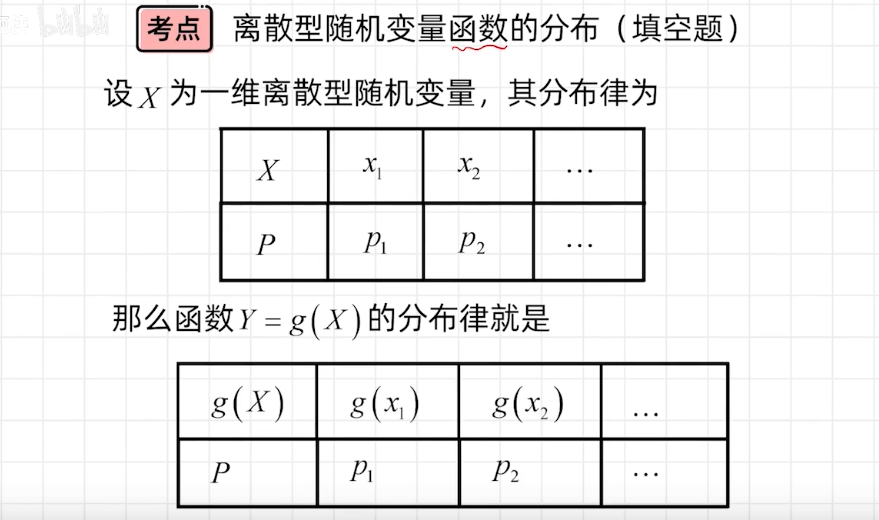
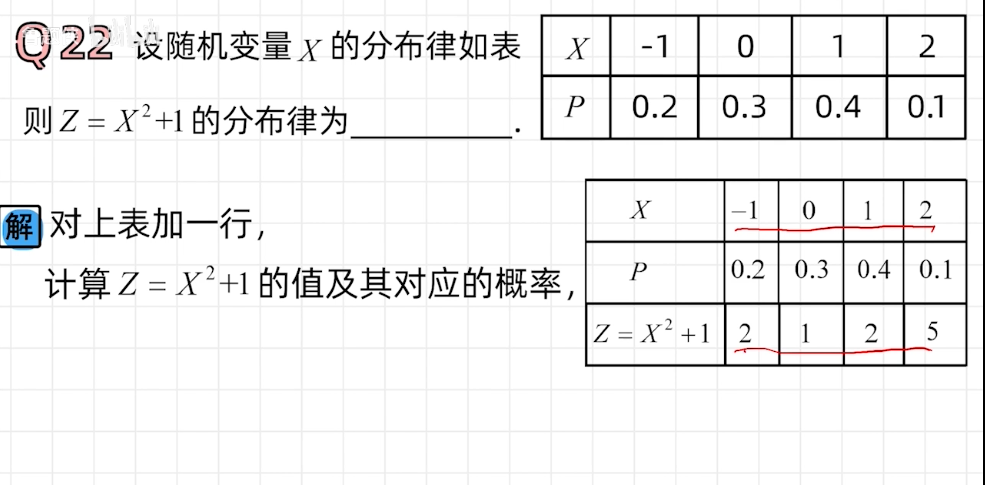

概率密度求概率密度
先积分,再求导


例题




二维离散型随机变量的分布
联合分布律
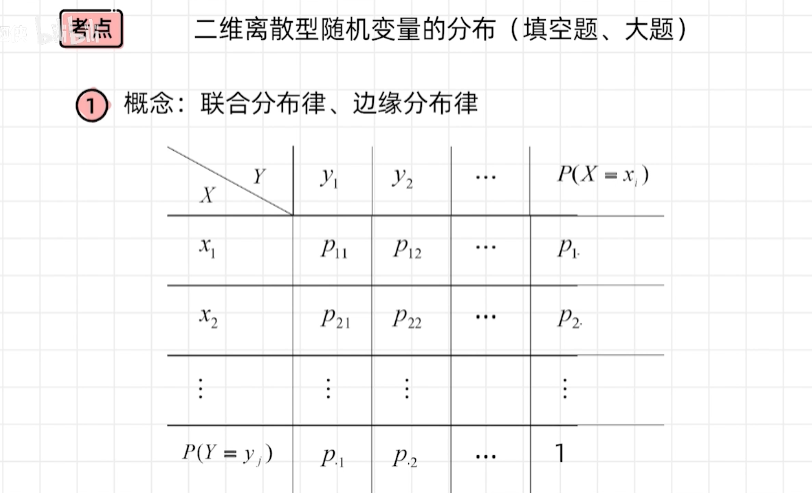
离散型用枚举法
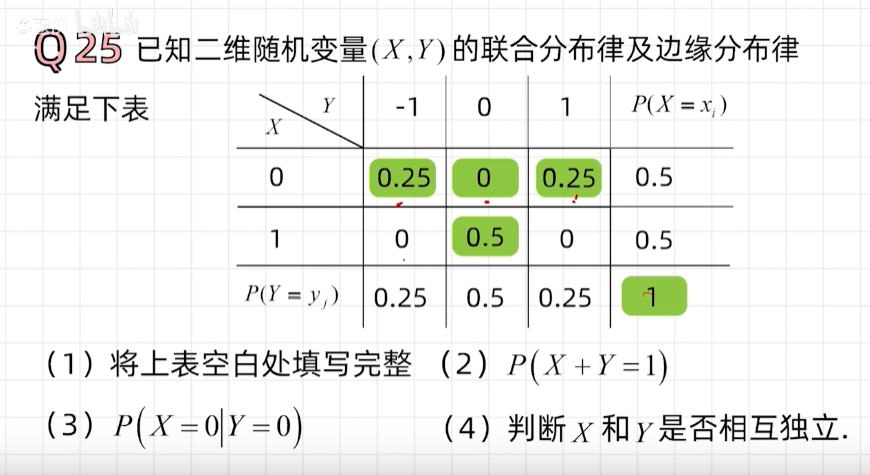


二维随机变量的的分布

例题



例题2:



离散型随机变量函数的分布


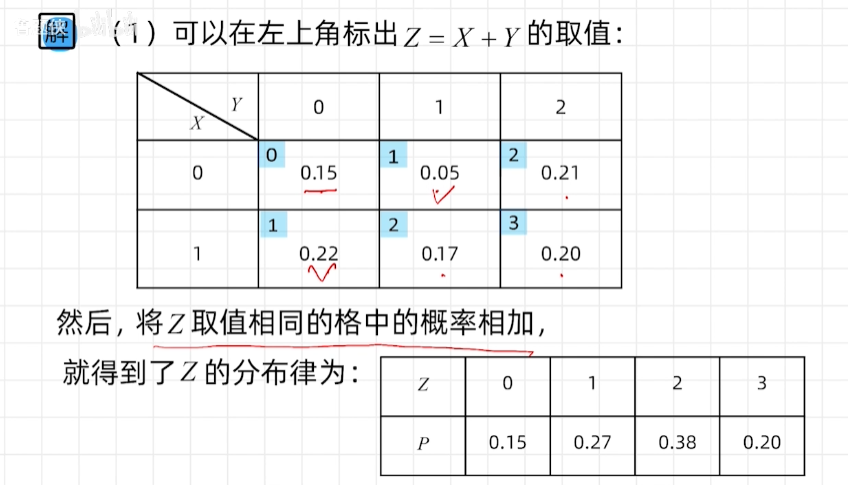
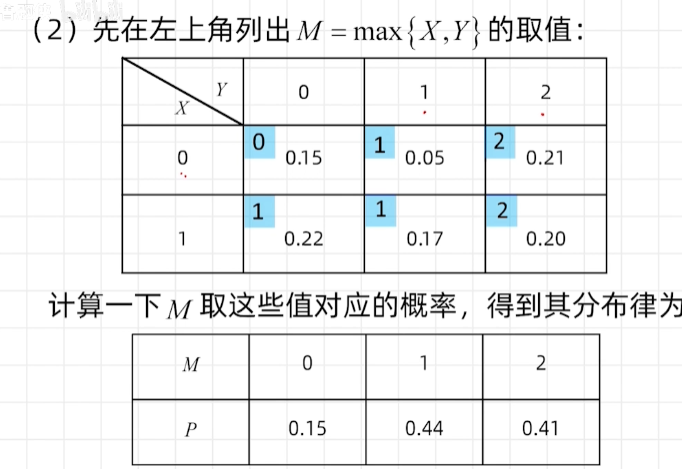
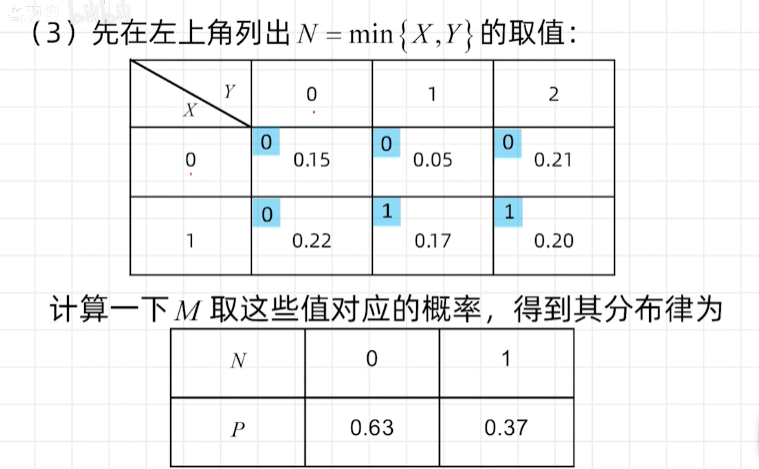
连续性随机变量函数的分布



正太分布可加性



例题2
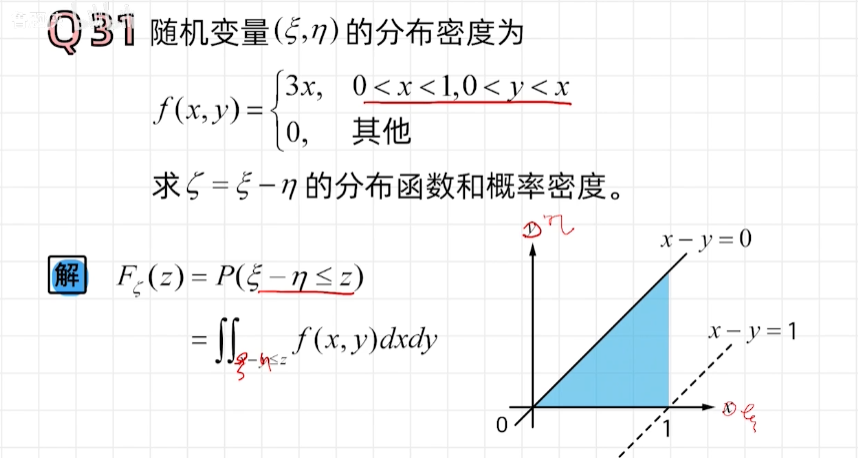
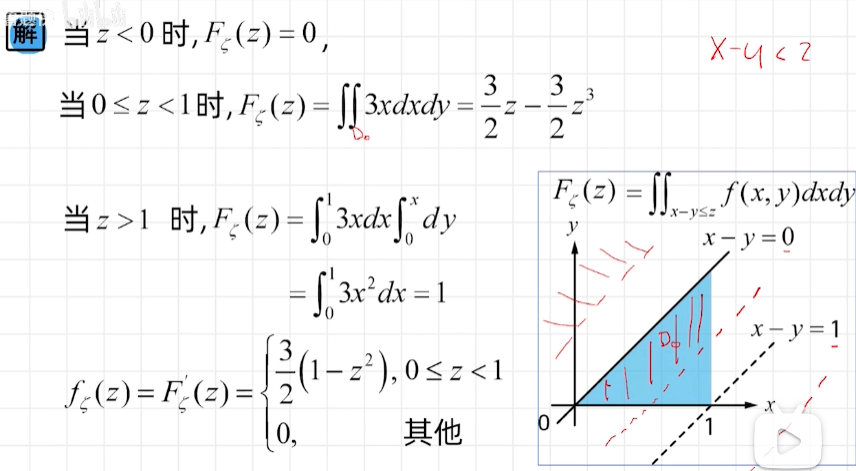
数学期望



方差和标准差



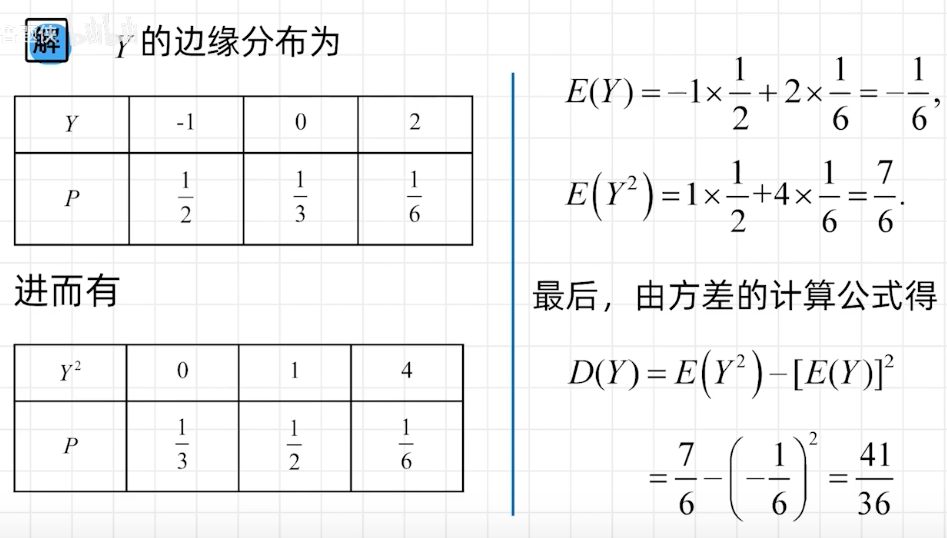
例题2

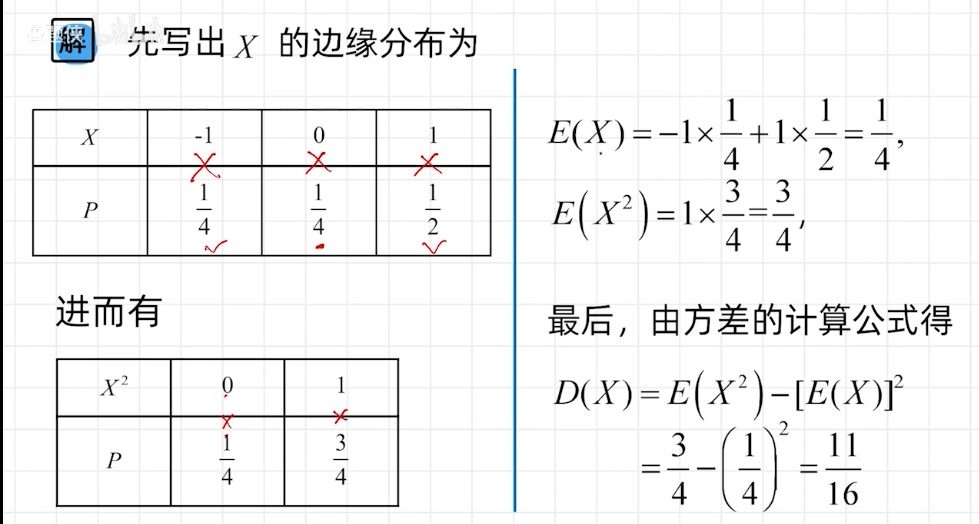
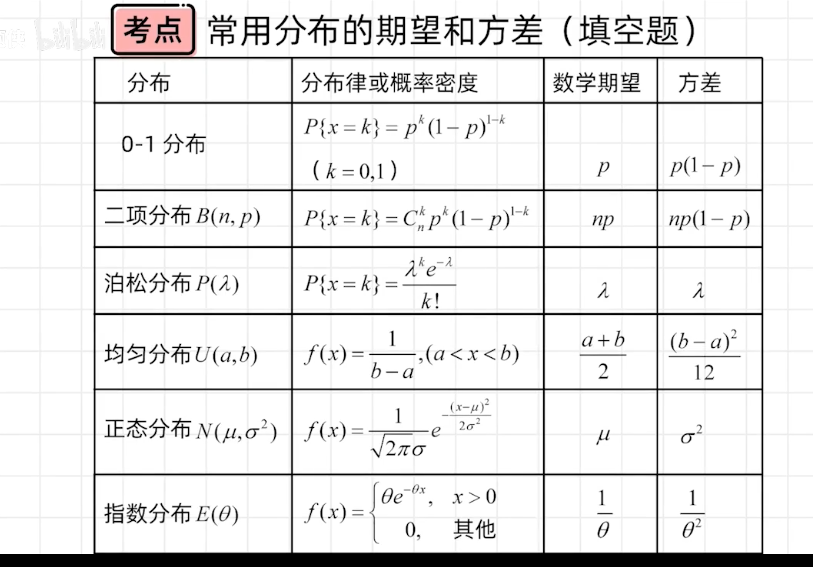
常见的随机变量的期望和方差



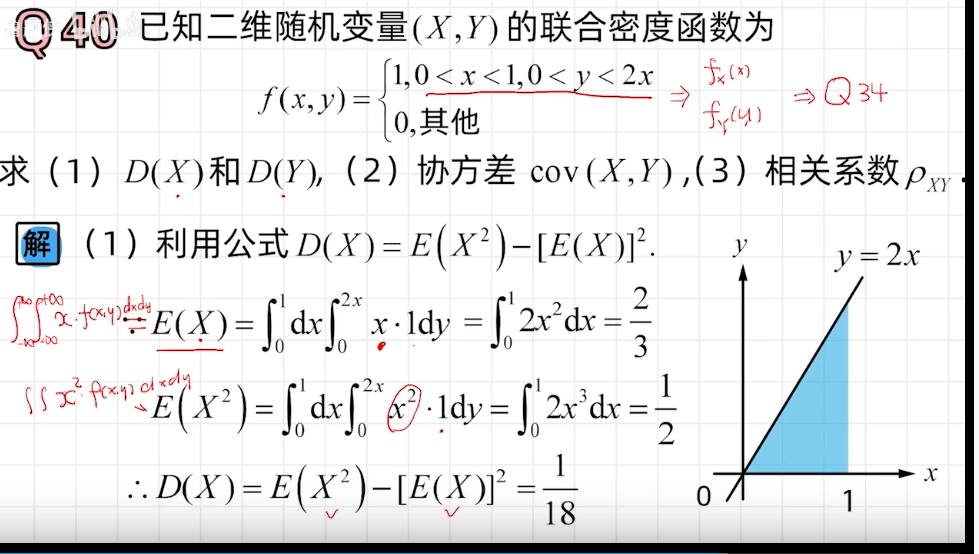
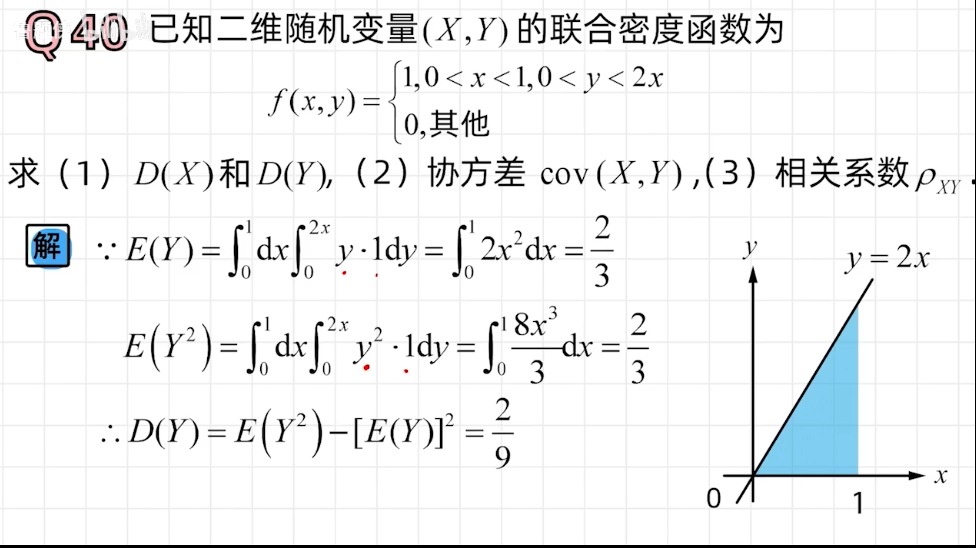
协方差和相关系数




二维离散型随机变量期望与方差的计算


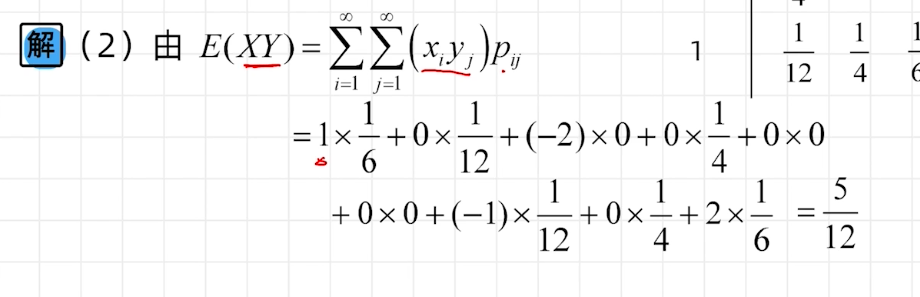
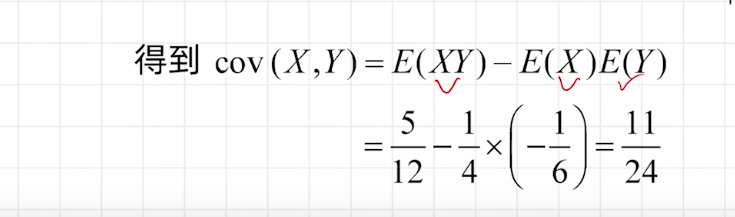
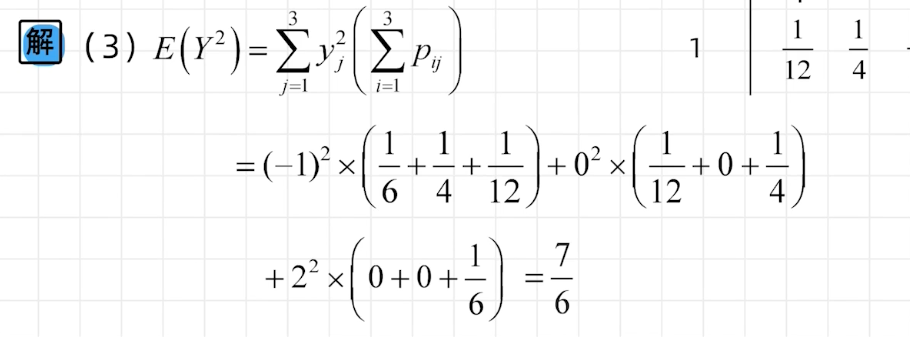
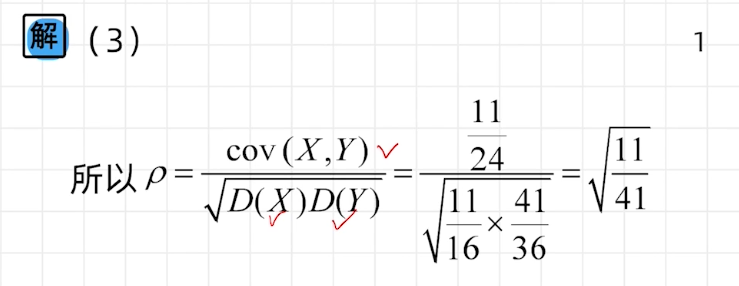
中心极限定理

将二项分布近似为正太分布
先根据二项分布求出期望和方差,然后根据期望与方差求u和C塔的平方



三大分布

例题
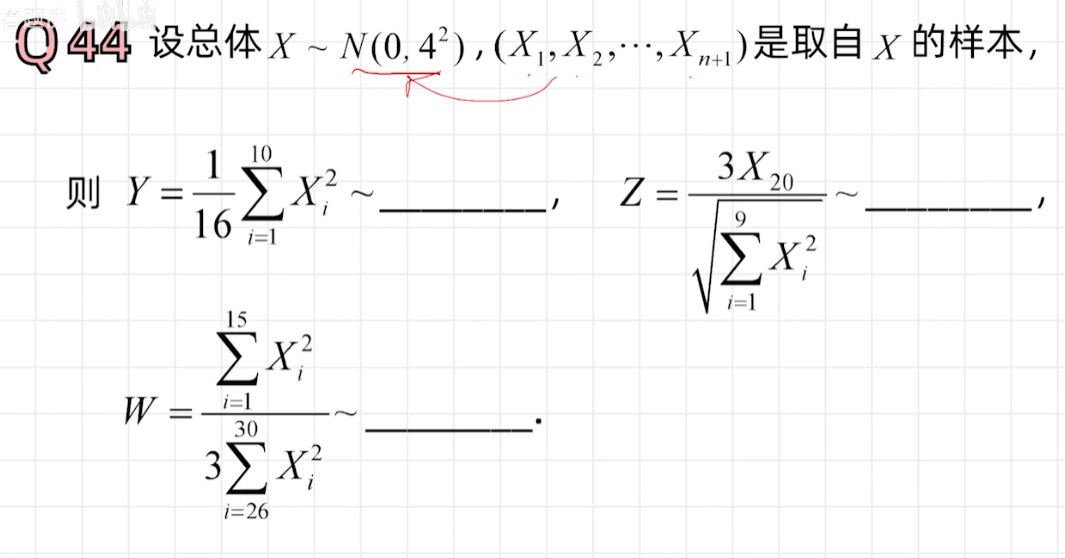
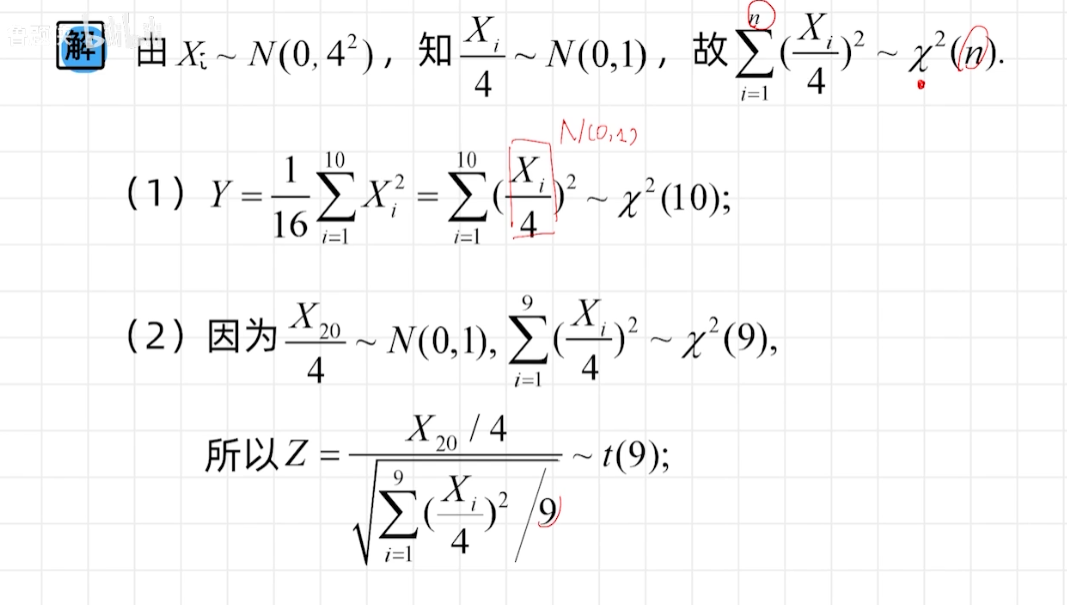
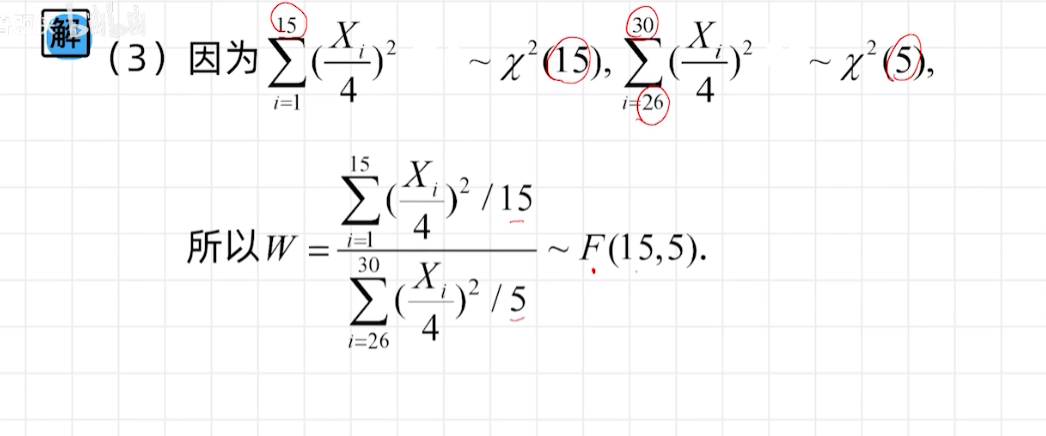
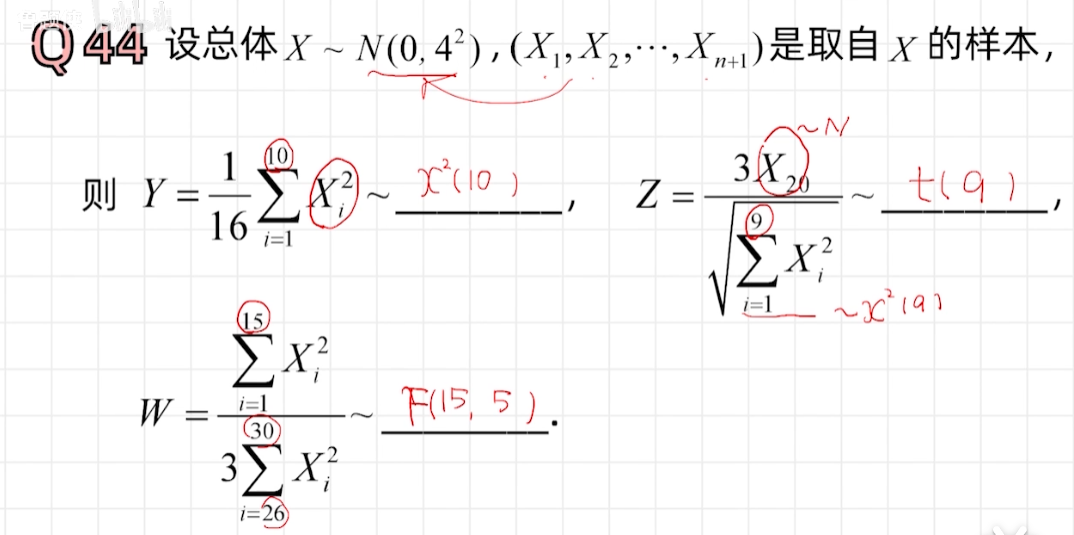
矩估计





极大似然估计
离散型




连续性

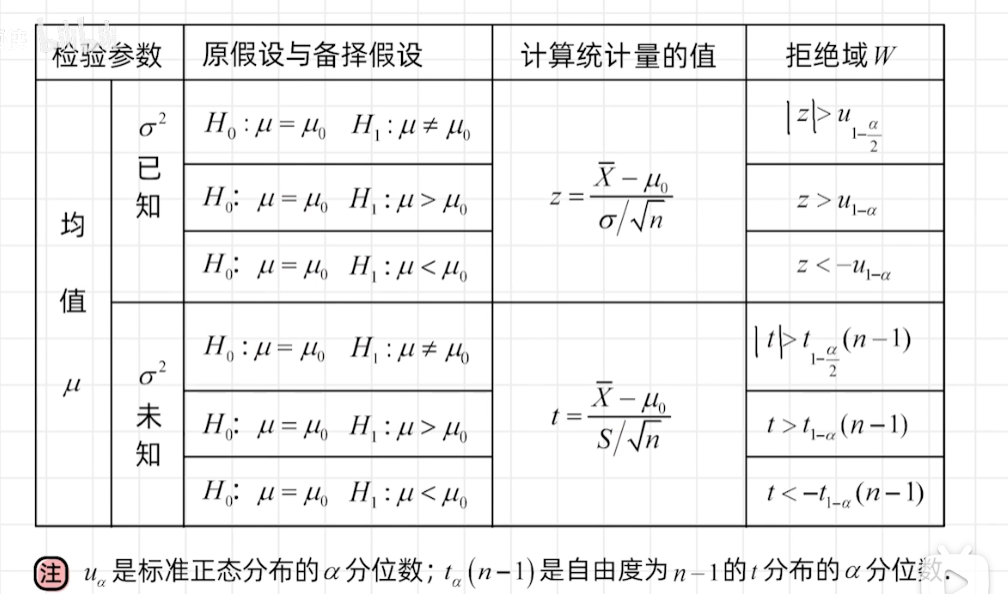
假设检验



-kOqQth5a-1640708495514)]
连续性

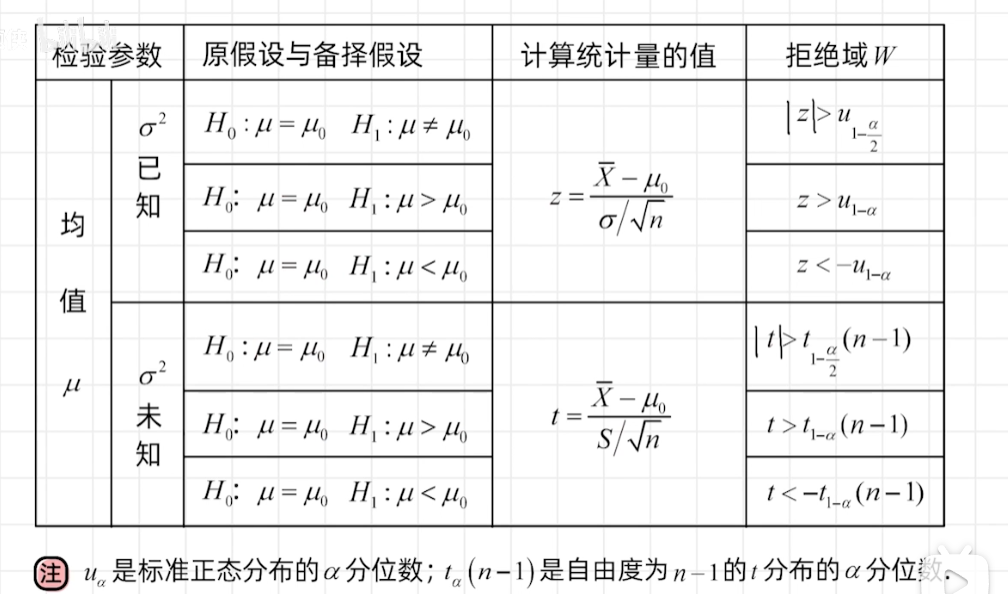
假设检验




本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!