波兰式转为逆波兰式——2016年华为笔试最后一题

题目

2016年9月6日华为笔试最后一道题（300分）为波兰式转化为逆波兰式的问题，具体题目为：

描述：
　　波兰表示法，是一种逻辑、算术和代数表示方法，其特点是操作符置于操作数的前面，因此也称为前缀表示法。例如：“a+b”的波兰表示法为：“+ab”。
　　逆波兰表示法是一种数学表达式方式，在逆波兰记法中，所有操作符置于操作数的后面，因此也称为后缀表示法。例如：“a+b”的逆波兰表示法为：“ab+”。
　　题目要求将输入的波兰表示法表达式转换为逆波兰表示法表达式。
说明：
　　给定输入和结果输出运算符和变量之间均用逗号隔开。题目给定的运算符仅有“+”、“-”、“*”、“/”四种。
示例输入（波兰式）：“-,+,a,*,+,b,c,d,e”
对应的中缀表达式：“a+(b+c)*d-e”
结果输出（逆波兰式）：“a,b,c,+,d,*,+,e,-,”

解题思路

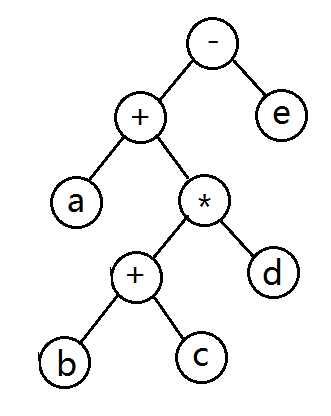
　　由上图二叉树我们可知，前缀表达式实际上是二叉树的前序遍历，后缀表达式实际上是二叉树的后续遍历。以上二叉树有一个特点，即叶子节点为字母（非操作符）。由此特点，若知道前序、中序、后序遍历中的任何一种，都可一还原上图二叉树。
由此，解题思路为：
1. 根据前缀表达式，构建二叉树；
2. 后序遍历该二叉树，即得到后缀表达式（逆波兰式）。

由于前序遍历是先根，后左右结点。在构建二叉树时，有如下规则：
1. 先确定根节点root。从左向右遍历前缀序列，根节点即为前缀序列的第一个字符，其值为“-”；
2. 第二个字符即为其左结点，其值为“+”；
3. 若第三个字符为操作符，则右结点为最后一个字符。否则为第三个字符；此例中为最后一个字符“e”;
4. 然后以左右结点中为操作符的结点作为根节点，重复1-3，即可还原二叉树。

代码实现

实现代码如下：

import java.util.Scanner;/*** Tile:* Author: zsd* Date: 16-9-6* Email:726679904@qq.com*/
class TreeNode {public TreeNode left;public TreeNode right;public String val;public TreeNode(String val) {this.val = val;}
}public class PreToPost {//后序遍历private static void scan(TreeNode tn){if(tn.left!=null) scan(tn.left);if(tn.right!=null) scan(tn.right);System.out.print(tn.val+",");}//还原二叉树private static TreeNode buildTree(String[]pres){TreeNode head = new TreeNode(pres[0]);TreeNode tmp = head;int len = pres.length;int flag = len-1;for (int i = 1,j=1; j < len/2+1; j++,i++) {//如果字符为操作符if ((pres[i].compareTo("a")<0||pres[i].compareTo("z")>0)                        ) {tmp.left = new TreeNode(pres[i]);tmp.right = new TreeNode(pres[flag--]);tmp = tmp.left;}else{tmp.left = new TreeNode(pres[i]);tmp.right = new TreeNode(pres[++i]);tmp = tmp.right;}}return head;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);while (sc.hasNext()) {String[] pres = sc.nextLine().split(",");TreeNode head = buildTree(pres);scan(head);}}
}

举一反三

由上方法，若题目改为已知后缀表达式，求前缀表达。
示例输入（逆波兰式）：“a,b,c,+,d,*,+,e,-”
对应的中缀表达式：“a+(b+c)*d-e”
结果输出（波兰式）：“-,+,a,*,+,b,c,d,e,”
此时，该如何构建二叉树呢？
构建二叉树时，要遵守如下规则：
1. 由后序遍历的特点，从逆波兰式由后向前遍历，根节点为“-”；
2. 第二个字符即为其右结点，其值为“+”；
3. 若第三个字符为操作符，则右结点为第三个字符，左结点为最前面的一个字符。否则右结点为第三个字符，左结点为第四个字符；此例中左结点为最前面的字符“a”，右结点为第三个字符“*”;
4. 然后以左右结点中为操作符的结点作为根节点，重复1-3，即可还原二叉树。

具体代码实现如下：

import java.util.Scanner;/*** Tile:* Author: zsd* Date: 16-9-6* Email：726679904@qq.com*/
public class PostToPre {private static void scan(TreeNode tn){System.out.print(tn.val+",");if(tn.left!=null) scan(tn.left);if(tn.right!=null) scan(tn.right);}//还原二叉树，注意还原二叉树的方法与上题中使用方法的差别private static TreeNode buildTree(String[]posts){int len = posts.length;TreeNode head = new TreeNode(posts[len-1]);TreeNode tmp = head;int flag = 0;for (int i = len-2,j=1; j < len/2+1; j++,i--) {if ((posts[i].compareTo("a")<0||posts[i].compareTo("z")>0)                        ) {tmp.right = new TreeNode(posts[i]);tmp.left = new TreeNode(posts[flag++]);tmp = tmp.right;}else{tmp.right = new TreeNode(posts[i]);tmp.left = new TreeNode(posts[--i]);tmp = tmp.left;}}return head;}public static void main(String[] args) {Scanner sc = new Scanner(System.in);while (sc.hasNext()) {String[] posts = sc.nextLine().split(",");TreeNode head = buildTree(posts);scan(head);}}
}

以上 实现仅为个人见解，如有更好的实现方式，请不吝指教。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！