插入排序算法详解(从后往前)
插入排序算法详解(从后往前)
A. 把最后一个元素当成一个降序数组-----降序
1.核心代码
for (int i = 0; i <numbers.length-1; i++) {//j的初始值的位置为倒数第二个元素位置-i,随着i的变化往前走//交换的最多次数为i+1次for (int j =numbers.length-2-i;j<numbers.length-1;j++) {if(numbers[j]<numbers[j+1]){int temp=numbers[j];numbers[j]=numbers[j+1];numbers[j+1]=temp;}else{break;}}
}
2.常见问题点分析
2.1 如何进行插入排序???
解决方案: 1.把最后一个元素当成降序数组
2.拿紧邻的元素p(左边紧邻)与降序数组组合一起当成成一个新数组
3.拿p与原数组里面的每一个数进行比较大小(比较顺序为从前往后)
若比它小,就进行交换(大者在前,为降序)
否则无需执行后面的循环操作了
此时可以把组合在一起的结果当成一个新的降序数组
否则的理由:因为p大于等于原降序数组里面的第一个元素了,
那么此时后面的继续比较就没有任何意义了(再这么比较也不会有任何变化的)
循环往复执行上述步骤2,3,直至满足循环次数=数组长度-1,循环才结束
2.2 插入排序的循环次数为多少?
解决方案:循环次数=数组长度-1
2.3 插入排序具体操作(数字是这么移动的)过程
以数组int[] a=[1,22,6,4,88]为列
| 排序次数 | 需要排序的数组部分 | 排序前的数组 | 排序后的数组 |
|---|---|---|---|
| 第1次 | [4,88] | [1,22,6,4,88] | [1,22,6,88,4] |
| 第2次 | [6,88,4] | [1,22,6,88,4] | [1,22,88,6,4] |
| 第3次 | [22,88,6,4] | [1,22,88,6,4] | [1,88,22,6,4] |
| 第4次 | [1,88,22,6,4] | [1,88,22,6,4] | [88,22,6,4,1] |
2.4 为什么核心代码第10行要使用break跳出当前循环???
解决方案:因为默认为降序,且紧邻元素p比原数组的第一个元素的数据都大,
那么就没有任何交换的必要了。
2.5 内层循环为啥是从numbers.length-2-i开始?
解答: a.每次都是从紧邻元素与原数组的第一个位置进行比较大小开始的
b.且每次新的紧邻元素会每次往前移动一个,这与i的变化规律一致
c.第一次的紧邻元素为倒数第二个即numbers.length-1-1
2.6 紧邻元素与降序数组组合一起的新数组需要进行比较大小几次,才能得到新的降序数组??
解答: 假设数组长度为5
当紧邻元素位置为numbers.length-1-0=4时,需要比较1次
当紧邻元素位置为numbers.length-1-1=3时,需要比较2次
…
当紧邻元素位置为numbers.length-1-i时,需要比较i+1次
因而需要比较i+1次(内层循环j不可以取值到最后一个元素)
3.运行截图

4.源代码
public class InsertSort03 {public static void main(String[] args) {//核心就是保证每次需要加入的新元素的位置能进行顺利往前移动System.out.println("插入排序之从后往前排序(尾元素为降序数组)");int[] numbers={1,22,6,4,88};System.out.println("排序前:");for (int temp01:numbers) {System.out.print(temp01+"\t");}for (int i = 0; i <numbers.length-1; i++) {for (int j =numbers.length-2-i;j<numbers.length-1;j++) {//保证大者位于靠前的位置if(numbers[j]<numbers[j+1]){int temp=numbers[j];numbers[j]=numbers[j+1];numbers[j+1]=temp;}else{break;}}System.out.println("\n第"+(i+1)+"次排序后");for (int temp02:numbers) {System.out.print(temp02+"\t");}}System.out.println("\n排序后:");for (int temp03:numbers) {System.out.print(temp03+"\t");}}
}
B. 把最后一个元素当成一个升序数组-----升序
1.核心代码
for (int i = 0; i <numbers.length-1; i++) {for (int j =numbers.length-2-i;j<numbers.length-1;j++) {//保证小者在前,为升序if(numbers[j]>numbers[j+1]){int temp=numbers[j];numbers[j]=numbers[j+1];numbers[j+1]=temp;}else{break;}}
}
2.常见问题点分析
2.1 如何进行插入排序???
解决方案: 1.把最后一个元素当成升序数组
2.拿紧邻的元素p与升序数组组合一起当成成一个新数组
3.拿p与原数组里面的每一个数进行比较大小,(比较大小的顺序为从前往后)
若比它大,就进行交换(小者在前,为升序)
否则无需执行后面的循环操作了,
此时可以把组合的结果当成一个新的升序数组
否则的理由:因为p小于等于原升序数组里面的第一个数字了,
那么此时后面的继续比较就没有任何意义了(再这么比较也不会有任何变化的)
循环往复执行上述步骤2,3,直至满足循环次数=数组长度-1,循环才结束
2.2 插入排序的循环次数为多少?
解决方案:循环次数=数组长度-1
2.3 插入排序具体操作(数字是这么移动的)过程
以数组int[] a=[16,11,18,9,8]为列
| 排序次数 | 需要排序的数组部分 | 排序前的数组 | 排序后的数组 |
|---|---|---|---|
| 第1次 | [9,8] | [16,11,18,9,8] | [16,11,18,8,9] |
| 第2次 | [18,8,9] | [16,11,18,8,9] | [16,11,8,9,18] |
| 第3次 | [11,8,9,18] | [16,11,8,9,18] | [16,8,9,11,18] |
| 第4次 | [16,8,9,11,18] | [16,8,9,11,18] | [8,9,11,16,18] |
2.4 为什么核心代码第9行要使用break跳出当前循环???
解决方案:因为默认有序为升序,且紧邻元素p比原数组的第一个数据都小,
那么就没有任何交换的必要了。
2.5 内层循环为啥是从numbers.length-2-i开始?
解答: a.每次都是从紧邻元素与原数组的第一个位置进行比较大小开始的
b.且每次新的紧邻元素会每次往前移动一个,这与i的变化规律一致
c.第一次的紧邻元素为倒数第二个即numbers.length-1-1
2.6 紧邻元素与升序数组组合一起的新数组需要进行比较大小几次,才能得到新的升序数组??
解答: 假设数组长度为5
当紧邻元素位置为numbers.length-1-0=4时,需要比较1次
当紧邻元素位置为numbers.length-1-1=3时,需要比较2次
…
当紧邻元素位置为numbers.length-1-i时,需要比较i+1次
因而需要比较i+1次(内层循环j不可以取值到最后一个元素)
3.运行截图
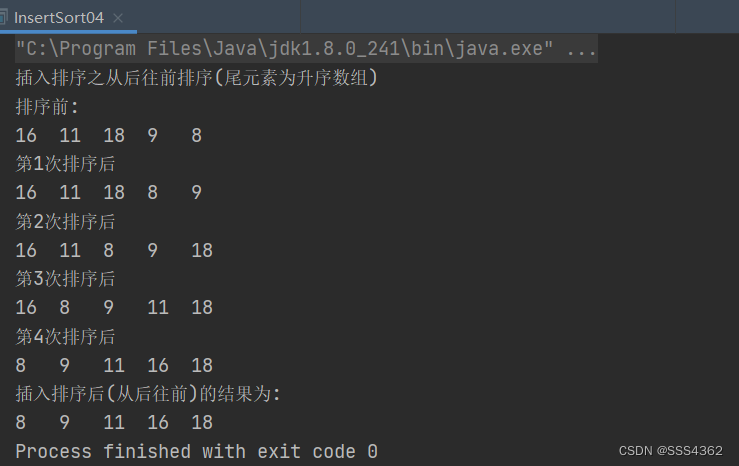
4.源代码
public class InsertSort04 {public static void main(String[] args) {//核心就是保证每次需要加入的新元素能进行顺利移动//内层循环通常比较次数为i+1次System.out.println("插入排序之从后往前排序(尾元素为升序数组)");int[] numbers={16,11,18,9,8};System.out.println("排序前:");for (int temp01:numbers) {System.out.print(temp01+"\t");}for (int i = 0; i <numbers.length-1; i++) {for (int j =numbers.length-2-i;j<numbers.length-1;j++) {if(numbers[j]>numbers[j+1]){int temp=numbers[j];numbers[j]=numbers[j+1];numbers[j+1]=temp;}else{break;}}System.out.println("\n第"+(i+1)+"次排序后");for (int temp02:numbers) {System.out.print(temp02+"\t");}}System.out.println("\n插入排序后(从后往前)的结果为:");for (int temp03:numbers) {System.out.print(temp03+"\t");}}
}
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!