实习生笔试

第一题：题目是一个长为n的数组（非负数），元素i左边找到比i大的最大值left_max，右边找到比i小的最大值right_max，如果left_max是right_max整数倍，则i是有价值的数，输出数组一共多少有价值的数？

刚开始我只想到暴力法（只通过了系统部分测试用例，时间复杂度太高了，没有AC）：

#include
#include
#include
using namespace std;
int main()
{int n;cin >> n;vector<int>a(n);for (int i = 0; i<n; i++)cin >> a[i];vector<int>left(n, -1);//left[i]记录a[i]左侧大于a[i]的最大数vector<int>right(n, -1);//right[i]记录a[i]右侧小于a[i]的最大数for (int i = 1; i<n; i++){for (int j = 0; j<i; j++){if (a[i]<a[j]){left[i] = max(left[i], a[j]);}}}for (int i = 0; i<n - 1; i++){for (int j = i + 1; j<n; j++){if (a[i]>a[j]){right[i] = max(right[i], a[j]);}}}int res = 0;for (int i = 1; i<n - 1; i++){if (left[i] != -1 && right[i] != -1)if (left[i] % right[i] == 0){res++;}}cout << res << endl;system("pause");return 0;}

后来交了卷马上就想到了改进方法，好气啊，为什么偏偏交卷了以后马上就想到了！！！，其实这题可以在暴力法的基础上加上一点动态规划的思路，就可以把算法时间复杂度从O（n²）降到O（n）。
自己改进后的代码如下：

int main()
{int n;cin >> n;vector<int>a(n);for (int i = 0; i < n; i++)cin >> a[i];vector<int>left(n, -1);//left[i]记录a[i]左侧大于a[i]的最大数vector<int>right(n, -1);//right[i]记录a[i]右侧小于a[i]的最大数//初始化if (a[1] < a[0])left[1] = a[0];if (a[n - 1] < a[n - 2])right[n - 2] = a[n - 1];for (int i = 2; i < n; i++){if (a[i] < a[i - 1]){left[i] = max(left[i - 1], a[i - 1]);}}for (int i = n-2; i >=0; i--){if (a[i] > a[i+1]){right[i] = max(right[i+1], a[i + 1]);}}int res = 0;for (int i = 1; i < n - 1; i++){if (left[i] != -1 && right[i] != -1)if (left[i] % right[i] == 0){res++;}}cout << res << endl;system("pause");return 0;}

第二题

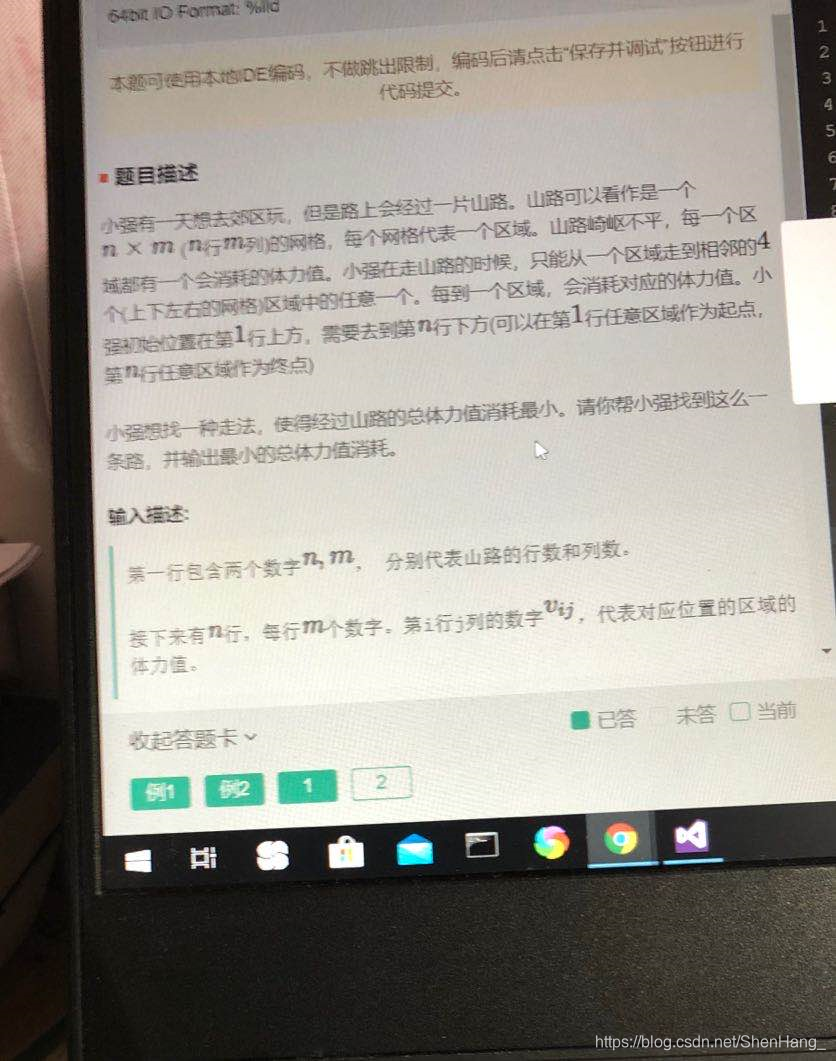
例如：
输入：
3 4
9 9 1 1
9 1 1 9
1 1 9 9
输出
4

我的思路是想用dp+回溯，但是感觉这题的难点在于起点和终点都是不确定的，我模型没建出来。只写了一部分代码。
后来我又想到思路了！！好气啊，就是简单的递归！！！

#include
#include
using namespace std;
const int INFINITE = 65536;
void DFS(const vector<vector<int>>&array, vector<vector<int>>&dp, int i, int j, int current_sum, int &res)
{//递归结束的条件if (i < 0 || j < 0 || j >= array[0].size()){return;}//递归结束的条件if (i<array.size() && array[i][j] + current_sum > dp[i][j])//如果此时同一个值已经被遍历过并且取值更小，则没必要再对它遍历{return;}//递归结束的条件if (i == array.size()){res = min(res, current_sum);return;}//表示当前格子是可以进入的//更新dpdp[i][j] = current_sum + array[i][j];//开启新的子递归DFS(array, dp, i + 1, j, current_sum + array[i][j], res);DFS(array, dp, i - 1, j, current_sum + array[i][j], res);DFS(array, dp, i, j + 1, current_sum + array[i][j], res);DFS(array, dp, i, j - 1, current_sum + array[i][j], res);}
int main()
{int res = INFINITE;int n, m;cin >> n >> m;vector<vector<int>>dp(n, vector<int>(m, INFINITE));//dp[i][j]表示从某个起点出发走到(i,j)消耗的体力最小值vector<vector<int>>array(n, vector<int>(m, 0));for (int i = 0; i < n; i++)for (int j = 0; j < m; j++){cin >> array[i][j];}for (int j = 0; j < m; j++)//m个起点{DFS(array, dp, 0, j, 0, res);}cout << res << endl;system("pause");return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！