JAVA 获取树的所有路径-深度优先遍历和广度优先

1、示例

树的结构

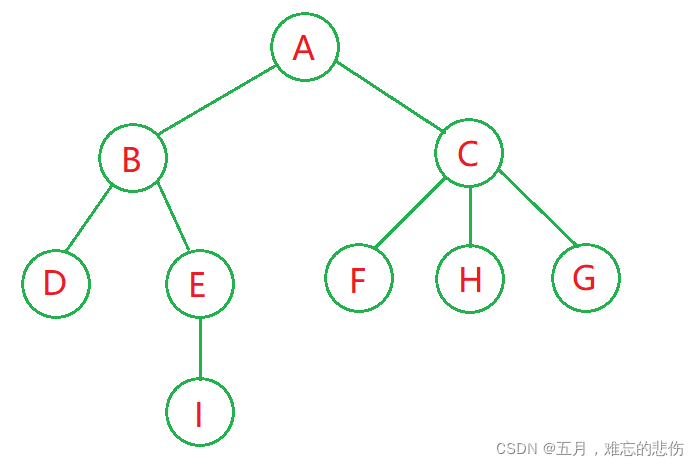
示例中本身构建了图片中的这棵树
树节点模型：

public class TreeNode {String value;List<TreeNode> children;public TreeNode() {children = new ArrayList<>();}public TreeNode(String value) {this.value = value;children = new ArrayList<>();}@Overridepublic String toString() {// TODO Auto-generated method stubreturn value;}
}

构建树：

// 建立一棵树
TreeNode root = new TreeNode("A");
// 第二层
root.children.add(new TreeNode("B"));
root.children.add(new TreeNode("C"));
// 第三层
root.children.get(0).children.add(new TreeNode("D"));
root.children.get(0).children.add(new TreeNode("E"));
root.children.get(1).children.add(new TreeNode("F"));
root.children.get(1).children.add(new TreeNode("H"));
root.children.get(1).children.add(new TreeNode("G"));
// 第四层
root.children.get(0).children.get(1).children.add(new TreeNode("I"));

2、遍历方式

① 递归形式的深度优先遍历

/*** 深度优先遍历（递归方式） --- 树（Tree）*/public void recurTree(TreeNode root) {List<List<String>> result = new ArrayList<>();List<String> path = new ArrayList<>();path.add(root.value);findPath(result, root, path);System.out.println(result);}private void findPath(List<List<String>> result, TreeNode node, List<String> path) {if (node.children == null || node.children.size() <= 0) {result.add(path);return;}for (int i = 0; i < node.children.size(); i++) {TreeNode child = node.children.get(i);List<String> cPath = new ArrayList<>();cPath.addAll(path);cPath.add(child.value);findPath(result, child, cPath, target);}}

② 非递归的深度优先遍历

/*** 深度优先遍历（非递归方式） ----- 查找树的全部叶子路径* * @param root*            根节点* @return 叶子路径的集合*/public List<List<TreeNode>> dfsTree(TreeNode root) {Stack<TreeNode> nodeStack = new Stack<>();Stack<List<TreeNode>> pathStack = new Stack<>();List<List<TreeNode>> result = new ArrayList<>();nodeStack.push(root);ArrayList<TreeNode> arrayList = new ArrayList<>();arrayList.add(root);pathStack.push(arrayList);while (!nodeStack.isEmpty()) {TreeNode curNode = nodeStack.pop();List<TreeNode> curPath = pathStack.pop();if (curNode.children == null || curNode.children.size() <= 0) {result.add(curPath);} else {int childSize = curNode.children.size();for (int i = childSize - 1; i >= 0; i--) {TreeNode node = curNode.children.get(i);nodeStack.push(node);List<TreeNode> list = new ArrayList<>(curPath);list.add(node);pathStack.push(list);}}}return result;}

③ 广度优先遍历，遍历全部叶子路径

/*** 广度优先遍历 ---- 查找树的全部叶子路径* * @param root*            根节点* @return 叶子路径的集合*/public List<List<TreeNode>> bfsTree(TreeNode root) {Queue<TreeNode> nodeQueue = new LinkedList<>();Queue<List<TreeNode>> qstr = new LinkedList<>();List<List<TreeNode>> result = new ArrayList<>();nodeQueue.add(root);ArrayList<TreeNode> arrayList = new ArrayList<>();qstr.add(arrayList);while (!nodeQueue.isEmpty()) {TreeNode curNode = nodeQueue.remove();List<TreeNode> curList = qstr.remove();if (curNode.children == null || curNode.children.size() <= 0) {curList.add(curNode);result.add(curList);} else {for (int i = 0; i < curNode.children.size(); i++) {TreeNode treeNode = curNode.children.get(i);nodeQueue.add(treeNode);List<TreeNode> list = new ArrayList<>(curList);list.add(curNode);qstr.add(list);}}}return result;}

三种方式的输出：

深度优先遍历（递归）：[[A, B, D], [A, B, E, I], [A, C, F], [A, C, H], [A, C, G]]
广度优先遍历：[[A, B, D], [A, C, F], [A, C, H], [A, C, G], [A, B, E, I]]
深度优先遍历（非递归）：[[A, B, D], [A, B, E, I], [A, C, F], [A, C, H], [A, C, G]]

3、查找分支

示例是查找树的全部叶子节点，触类旁通，若是咱们是查找树中知足某个条件的路径，也是很是容易了。好比下面中查找 “ E ” 的分支：

public void recurTree(TreeNode root) {List<List<String>> result = new ArrayList<>();List<String> path = new ArrayList<>();path.add(root.value);findPath(result, root, path, "E");System.out.println(result);}private void findPath(List<List<String>> result, TreeNode node, List<String> path, String target) {if (target.equals(node.value)) {result.add(path);return;}if (node.children == null || node.children.size() <= 0) {return;}for (int i = 0; i < node.children.size(); i++) {TreeNode child = node.children.get(i);List<String> cPath = new ArrayList<>();cPath.addAll(path);cPath.add(child.value);if (result.size() > 0)break;findPath(result, child, cPath, target);}}

输出

[[A, B, E]]

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！