[CV] Rotated IoU 计算旋转矩形之间的重叠面积

文章目录

• [CV] Rotated IoU 计算旋转矩形之间的重叠面积
• • 简介
  • 旋转包围盒的编码方式
  • • 矢量的旋转公式
    • 包围盒转化为角点
    • 代码表示
  • 相交区域的特点
  • • 点在四边形(矩形)内
    • • 点积的物理意义
      • 代码
    • 线段交点
    • • 判断线段是否相交
      • 相交后转化为直线交点
      • 代码
  • 计算相交区域面积
  • • 顶点排序
    • • 顶点排序代码
    • 简易版三角剖分
  • 所有代码

简介

在目标检测的领域，基于Anchor的方法需要对Anchor分配正负样本的标签。通常，对于axis-aligned的anchor和ground truth，可以直接通过 [top left right down]四个值计算他们之间的重叠面积。但是针对于旋转的矩形框，这个问题就变得尤为复杂。

我参考了3D目标检测论文SECOND的源码，来尝试解释一下如何计算旋转包围盒的重叠面积。

代码全部来自second.pytorch这个项目的早期版本，去掉了numba/cuda加速的代码。

旋转包围盒的编码方式

作者代码使用了两种方式

1. 通过包围盒中心点位置，尺度以及角度来编码rbbox

rbbox = [x, y, x_d (w), y_d (h), angle]

2. 通过包围盒的顶点corners来编码

矢量的旋转公式

将矢量看作列矢量 α ⃗ ∈ R 2 × 1 \vec{\alpha}\in \mathbb R^{2\times1} α ∈R2×1， 则将其逆时针旋转$\theta$ 之后的矢量为：

[ cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ ] α ⃗ \begin{bmatrix}\cos\theta&-\sin\theta\\ \sin\theta & \cos\theta\end{bmatrix}\vec{\alpha} [cosθsinθ​−sinθcosθ​]α

包围盒转化为角点

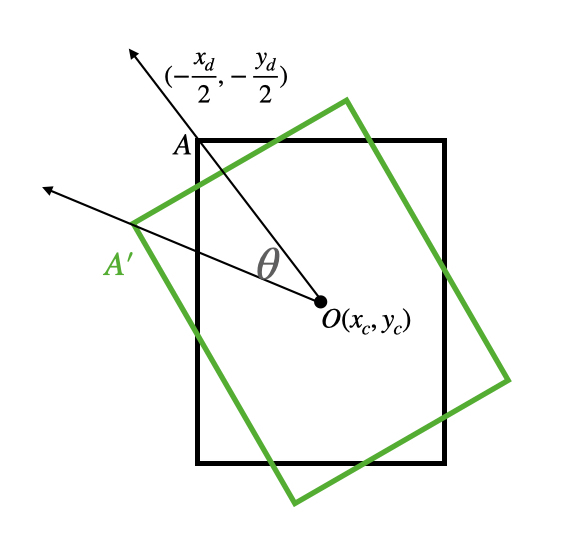
如图，rbbox为绿色的包围盒，是原始黑色包围盒通过逆时针旋转$\theta$角度得到。分析 $A’$ 的真实坐标：

首先向量 O A → \overrightarrow{OA} OA 被表示为

O A → = [ − x d 2 , − y d 2 ] T \overrightarrow{OA} = [-\frac{x_d}{2}, -\frac{y_d}{2}]^T OA =[−2xd​​,−2yd​​]T

旋转后的向量可以被表示为

O A ′ → = T θ O A → = [ cos ⁡ θ ⋅ − x d 2 − sin ⁡ θ − y d 2 sin ⁡ θ − x d 2 + cos ⁡ θ − y d 2 ] \overrightarrow{OA'} = T_\theta\overrightarrow{OA} = \begin{bmatrix} \cos\theta\cdot\frac{-x_d}{2} -\sin\theta\frac{-y_d}{2}\\ \sin\theta \frac{-x_d}{2} + \cos\theta\frac{-y_d}{2}\end{bmatrix} OA′ =Tθ​OA =[cosθ⋅2−xd​​−sinθ2−yd​​sinθ2−xd​​+cosθ2−yd​​​]
通过 A ’ = O + O A ’ → A’ = O + \overrightarrow{OA’} A’=O+OA’ 恢复顶点的坐标即可。

代码表示

下段代码将[x, y, x_d, y_d, angle]转化为顺时针方方向表示的顶点坐标[x0, y0, x1, y1, x2, y2, x3, y3]

import math
def rbbox_to_corners(rbbox):# generate clockwise corners and rotate it clockwise# 顺时针方向返回角点位置cx, cy, x_d, y_d, angle = rbboxa_cos = math.cos(angle)a_sin = math.sin(angle)corners_x = [-x_d / 2, -x_d / 2, x_d / 2, x_d / 2]corners_y = [-y_d / 2, y_d / 2, y_d / 2, -y_d / 2]corners = [0] * 8for i in range(4):corners[2 *i] = a_cos * corners_x[i] + \a_sin * corners_y[i] + cxcorners[2 * i +1] = -a_sin * corners_x[i] + \a_cos * corners_y[i] + cyreturn corners

测试一下结果：

rbbox = [0, 0, 2, 4, math.pi / 2]
corners = rbbox_to_corners(rbbox)
print([round(_) for _ in corners])
# [-2, 1, 2, 1, 2, -1, -2, -1]

相交区域的特点

两个四边形(矩形)，求交叠面积，可以先求出相交的多边形(Polygon)的顶点, 构成多边形的顶点可由两种类型的点构成：

1. 原始四边形的顶点
2. 四边形的边相交产生的交点

对应问题为：

1. 判断点在四边形内
2. 判断线段的交点

点在四边形(矩形)内

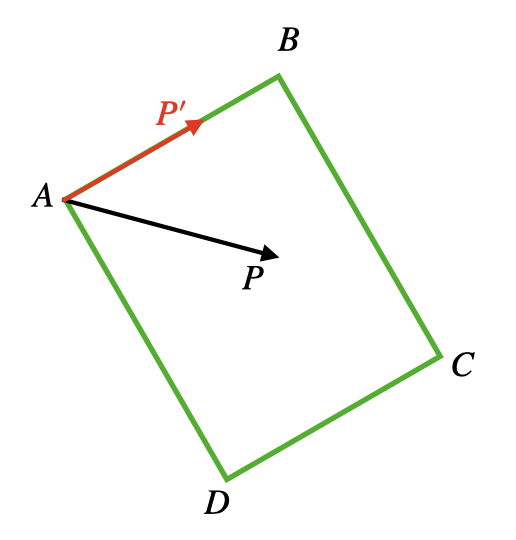
如图所示，四边形(矩形)通过ABCD四个顶点表示，可以使用较强的规则判断P在矩形内，即AP在AB 的投影在线段AB上，在AD的投影在线段AD上。

点积的物理意义

两个矢量的点积是标量，点积满足交换律：

1. 矢量的模被定义为 ∣ a ∣ = a ⋅ a |a|=\sqrt{a\cdot a} ∣a∣=a⋅a ​
2. $a\cdot b=|a||b|\cos \theta$ 实际表示为$b$在$a$上的投影的长度。如果投影与$a$方向相反，则为负值

所以代码的思路就是，通过点击得到投影长度，通过判断投影长度确定点在矩形框内。

代码

SECOND函数为 point_in_quadrilateral

def point_in_quadrilateral(pt_x, pt_y, corners):ab0 = corners[2] - corners[0]ab1 = corners[3] - corners[1]ad0 = corners[6] - corners[0]ad1 = corners[7] - corners[1]ap0 = pt_x - corners[0]ap1 = pt_y - corners[1]abab = ab0 * ab0 + ab1 * ab1abap = ab0 * ap0 + ab1 * ap1adad = ad0 * ad0 + ad1 * ad1adap = ad0 * ap0 + ad1 * ap1return abab >= abap and abap >= 0 and adad >= adap and adap >= 0

线段交点

判断线段是否相交

参考：判断线段相交的最简方法]

对于两个直线是否相交，一种方法是计算线段斜率，首先确定不平行，然后联立方程，计算交点坐标，最后运用定比分点公式，判断交点是否在线段上。但是使用斜率和定比分点，可能会出现精度丢失的现象，同时浮点数运算耗时。

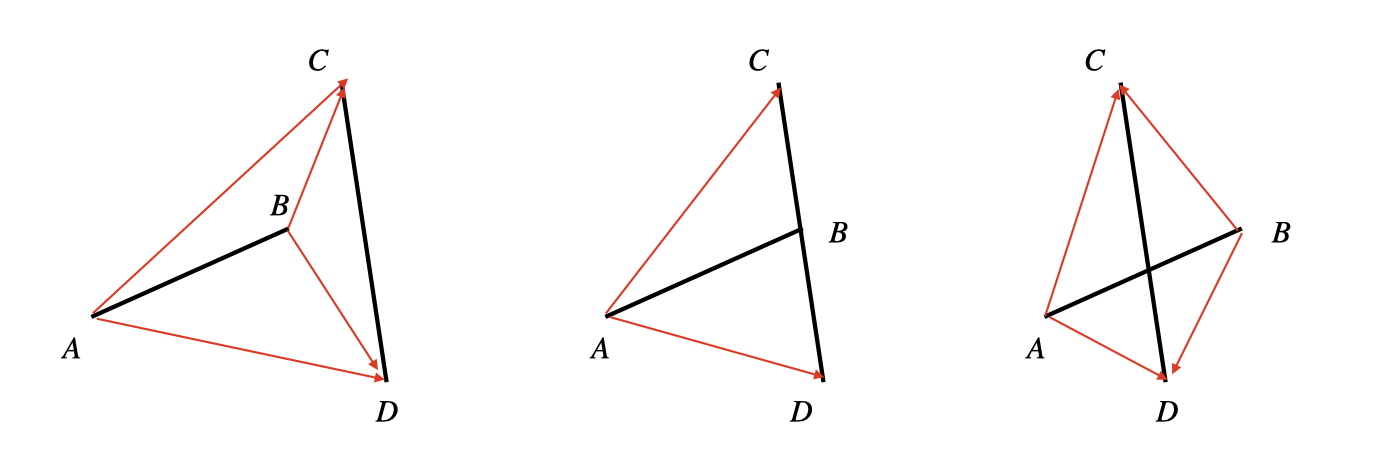
上图可以表示两个线段位置的所有可能情况。定义direct(a, b) 为向量有序对的旋转方向。其旋转方向为 使 a 能够旋转一个小于 180 度的角并与 b 重合的方向，简记为 direct(a, b)。若 a 和 b 反向共线，则旋转方向取任意值。

则上图三种情况可以概括为：

1. direct(AC, AD) 和 direct(BC, BD) 为顺时针，direct(CA, CB) 为逆时针，direct(DA, DB)为顺时针
2. direct(AC, AD)顺时针， direct(BC, BD)为任意方向，direct(CA, CB)为逆时针，direct(DA, DB) 为顺时针
3. direct(AC, AD) 和 direct(DA, DB) 为顺时针，direct(BC, BD) 和 direct(CA, CB) 为逆时针

可以得知，两条线段相交的充要条件是direct(AC, AD) != direct(BC, BD) 和 direct(CA, CB) != direct(DA, DB)

定义 < a ⃗ , b ⃗ > <\vec{a}, \vec{b}> <a ,b > 为 a ⃗ \vec{a} a 逆时针旋转到与 b ⃗ \vec{b} b 重合的角度。有：

• direct(a, b) 顺时针, 0 ≤ < a ⃗ , b ⃗ > ≤ 180 0\le<\vec{a}, \vec{b}>\le180 0≤<a ,b >≤180, sin ⁡ < a ⃗ , b ⃗ > ≥ 0 \sin<\vec{a}, \vec{b}> \ge0 sin<a ,b >≥0
• direct(a, b) 逆时针, 180 ≤ < a ⃗ , b ⃗ > ≤ 360 180\le<\vec{a}, \vec{b}>\le360 180≤<a ,b >≤360, sin ⁡ < a ⃗ , b ⃗ > ≤ 0 \sin<\vec{a}, \vec{b}>\le0 sin<a ,b >≤0

问题可以转化为有向角正弦值的问题。可以使用叉乘来做:
a ⃗ × b ⃗ = a x ⋅ b y − a y ⋅ b x \vec{a}\times\vec{b}=a_x\cdot b_y - a_y \cdot b_x a ×b =ax​⋅by​−ay​⋅bx​
叉乘表示 a ⃗ , b ⃗ \vec{a}, \vec{b} a ,b 构成平行四边行的有向面积
∣ a ⃗ × b ⃗ ∣ = ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ ⋅ sin ⁡ θ |\vec{a}\times\vec{b}|=|\vec{a}|\cdot|\vec{b}|\cdot\sin\theta ∣a ×b ∣=∣a ∣⋅∣b ∣⋅sinθ

• 伸出右手，将四指由 a ⃗ \vec{a} a 沿小于平角转到 b ⃗ \vec{b} b 。若拇指指向纸面上方，则 a ⃗ × b ⃗ \vec{a}\times\vec{b} a ×b 为正，否则为负。

• 若向量共线，叉积为0

叉积的正负可以判断 < a ⃗ , b ⃗ > <\vec{a},\vec{b}> <a ,b > 的角度范围。所以充要条件等价于叉积符号不同。

相交后转化为直线交点

Wiki Line–line intersection

Using homogeneous coordinates

直接用wiki的结论，两个点可以确定一条直线，因此定义两条直线 ( x 1 , y 1 ) ( x 2 , y 2 ) (x_1, y_1) (x_2, y_2) (x1​,y1​)(x2​,y2​) 和 ( x 3 , y 3 ) ( x 4 , y 4 ) (x_3, y_3) (x_4, y_4) (x3​,y3​)(x4​,y4​) ，可以通过以下公式计算交点的坐标 ( P x , P y ) (P_x, P_y) (Px​,Py​)
P x = ( x 1 y 2 − y 1 x 2 ) ( x 3 − x 4 ) − ( x 1 − x 2 ) ( x 3 y 4 − y 3 x 4 ) ( x 1 − x 2 ) ( y 3 − y 4 ) − ( y 1 − y 2 ) ( x 3 − x 4 ) P_x = \frac{(x_1y_2 - y_1x_2)(x_3 -x_4) - (x_1 - x_2)(x_3y_4 - y_3x_4)}{(x_1-x_2)(y_3-y_4) - (y_1-y_2)(x_3 - x_4)} Px​=(x1​−x2​)(y3​−y4​)−(y1​−y2​)(x3​−x4​)(x1​y2​−y1​x2​)(x3​−x4​)−(x1​−x2​)(x3​y4​−y3​x4​)​

P y = ( x 1 y 2 − y 1 x 2 ) ( y 3 − y 4 ) − ( y 1 − y 2 ) ( x 3 y 4 − y 3 x 4 ) ( x 1 − x 2 ) ( y 3 − y 4 ) − ( y 1 − y 2 ) ( x 3 − x 4 ) P_y = \frac{(x_1y_2-y_1x_2)(y_3-y_4) - (y_1-y_2)(x_3y_4-y_3x_4)}{(x_1-x_2)(y_3-y_4) - (y_1-y_2)(x_3-x_4)} Py​=(x1​−x2​)(y3​−y4​)−(y1​−y2​)(x3​−x4​)(x1​y2​−y1​x2​)(y3​−y4​)−(y1​−y2​)(x3​y4​−y3​x4​)​

代码

代码如下

def line_segment_intersection(pts1, pts2, i, j):# pts1, pts2 为corners# i j 分别表示第几个交点，取其和其后一个点构成的线段# 返回为 tuple(bool, pts) bool=True pts为交点A, B, C, D, ret = [0, 0], [0, 0], [0, 0], [0, 0], [0, 0]A[0] = pts1[2 * i]A[1] = pts1[2 * i + 1]B[0] = pts1[2 * ((i + 1) % 4)]B[1] = pts1[2 * ((i + 1) % 4) + 1]C[0] = pts2[2 * j]C[1] = pts2[2 * j + 1]D[0] = pts2[2 * ((j + 1) % 4)]D[1] = pts2[2 * ((j + 1) % 4) + 1]BA0 = B[0] - A[0]BA1 = B[1] - A[1]DA0 = D[0] - A[0]CA0 = C[0] - A[0]DA1 = D[1] - A[1]CA1 = C[1] - A[1]# 叉乘判断方向acd = DA1 * CA0 > CA1 * DA0bcd = (D[1] - B[1]) * (C[0] - B[0]) > (C[1] - B[1]) * (D[0] - B[0])if acd != bcd:abc = CA1 * BA0 > BA1 * CA0abd = DA1 * BA0 > BA1 * DA0# 判断方向if abc != abd:DC0 = D[0] - C[0]DC1 = D[1] - C[1]ABBA = A[0] * B[1] - B[0] * A[1]CDDC = C[0] * D[1] - D[0] * C[1]DH = BA1 * DC0 - BA0 * DC1Dx = ABBA * DC0 - BA0 * CDDCDy = ABBA * DC1 - BA1 * CDDCret[0] = Dx / DHret[1] = Dy / DHreturn True, retreturn False, ret

测试结果:

if __name__ == '__main__':rbbox1 = [0, 0, 2, 4, 0]rbbox2 = [0, 0, 4, 2, 0]corners1 = rbbox_to_corners(rbbox1)corners2 = rbbox_to_corners(rbbox2)for i in range(4):for j in range(4):ret, pts = line_segment_intersection(corners1, corners2, i, j)if ret:print('Px: {}, Py: {}'.format(*pts))
"""
Px: -1.0, Py: 1.0
Px: -1.0, Py: -1.0
Px: 1.0, Py: 1.0
Px: 1.0, Py: -1.0
"""

计算相交区域面积

当有了构成相交区域多边行的顶点后，可以通过以下两部分计算相交区域的面积：

1. 将顶点按照顺时针或者逆时针排序
2. 三角剖分计算面积

顶点排序

在凸多边形内部取一点，与顶点连线，可以通过连线与坐标轴构成的角度排序。操作如下

1. 计算所有顶点的横纵坐标均值，记作中心点
2. 计算中心点到每个单位向量[vx, vy]。
3. 以x轴正方向为其实遍，按照顺时针方向扫描360度，对扫描到的点进行排序

关于步骤3，具体操作为：对于已经归一化单位向量，先考虑从180度到360度，有 v y ≥ 0 v_y\ge0 vy​≥0, − 1 < v x < 1 -1 −1<vx​<1， v x v_x vx​单增。对于从0到180度，有 v y < 0 v_y<0 vy​<0, − 1 < v x < 1 -1 < v_x < 1 −1<vx​<1, 其变化范围是由1到-1(单减)。则排序使用索引k可以为：

1. v y > 0 , k = v x v_y >0, k = v_x vy​>0,k=vx​
2. v y < 0 , k = − 2 − v x v_y < 0, k = -2-v_x vy​<0,k=−2−vx​

顶点排序代码

def sort_vertex_in_convex_polygon(int_pts, num_of_inter):def _cmp(pt, center):vx = pt[0] - center[0]vy = pt[1] - center[1]d = math.sqrt(vx * vx + vy * vy)vx /= dvy /= dif vy < 0:vx = -2 - vxreturn vxif num_of_inter > 0:center = [0, 0]for i in range(num_of_inter):center[0] += int_pts[i][0]center[1] += int_pts[i][1]center[0] /= num_of_intercenter[1] /= num_of_interint_pts.sort(key=lambda x: _cmp(x, center))

简易版三角剖分

将多边形转化为多个三角形面积之和，具体操作为固定一个点，按照顺时针顺序依次选择剩下的2个点，计算三角形面积(利用叉积) 最后将三角形面积求和。

代码如下：

def area(int_pts, num_of_inter):def _trangle_area(a, b, c):return ((a[0] - c[0]) * (b[1] - c[1]) - (a[1] - c[1]) *(b[0] - c[0])) / 2.0area_val = 0.0for i in range(num_of_inter - 2):area_val += abs(_trangle_area(int_pts[0], int_pts[i + 1],int_pts[i + 2]))return area_val

所有代码

代码汇总如下

import mathdef rbbox_to_corners(rbbox):# generate clockwise corners and rotate it clockwise# 顺时针方向返回角点位置cx, cy, x_d, y_d, angle = rbboxa_cos = math.cos(angle)a_sin = math.sin(angle)corners_x = [-x_d / 2, -x_d / 2, x_d / 2, x_d / 2]corners_y = [-y_d / 2, y_d / 2, y_d / 2, -y_d / 2]corners = [0] * 8for i in range(4):corners[2 *i] = a_cos * corners_x[i] + \a_sin * corners_y[i] + cxcorners[2 * i +1] = -a_sin * corners_x[i] + \a_cos * corners_y[i] + cyreturn cornersdef point_in_quadrilateral(pt_x, pt_y, corners):ab0 = corners[2] - corners[0]ab1 = corners[3] - corners[1]ad0 = corners[6] - corners[0]ad1 = corners[7] - corners[1]ap0 = pt_x - corners[0]ap1 = pt_y - corners[1]abab = ab0 * ab0 + ab1 * ab1abap = ab0 * ap0 + ab1 * ap1adad = ad0 * ad0 + ad1 * ad1adap = ad0 * ap0 + ad1 * ap1return abab >= abap and abap >= 0 and adad >= adap and adap >= 0def line_segment_intersection(pts1, pts2, i, j):# pts1, pts2 为corners# i j 分别表示第几个交点，取其和其后一个点构成的线段# 返回为 tuple(bool, pts) bool=True pts为交点A, B, C, D, ret = [0, 0], [0, 0], [0, 0], [0, 0], [0, 0]A[0] = pts1[2 * i]A[1] = pts1[2 * i + 1]B[0] = pts1[2 * ((i + 1) % 4)]B[1] = pts1[2 * ((i + 1) % 4) + 1]C[0] = pts2[2 * j]C[1] = pts2[2 * j + 1]D[0] = pts2[2 * ((j + 1) % 4)]D[1] = pts2[2 * ((j + 1) % 4) + 1]BA0 = B[0] - A[0]BA1 = B[1] - A[1]DA0 = D[0] - A[0]CA0 = C[0] - A[0]DA1 = D[1] - A[1]CA1 = C[1] - A[1]# 叉乘判断方向acd = DA1 * CA0 > CA1 * DA0bcd = (D[1] - B[1]) * (C[0] - B[0]) > (C[1] - B[1]) * (D[0] - B[0])if acd != bcd:abc = CA1 * BA0 > BA1 * CA0abd = DA1 * BA0 > BA1 * DA0# 判断方向if abc != abd:DC0 = D[0] - C[0]DC1 = D[1] - C[1]ABBA = A[0] * B[1] - B[0] * A[1]CDDC = C[0] * D[1] - D[0] * C[1]DH = BA1 * DC0 - BA0 * DC1Dx = ABBA * DC0 - BA0 * CDDCDy = ABBA * DC1 - BA1 * CDDCret[0] = Dx / DHret[1] = Dy / DHreturn True, retreturn False, retdef sort_vertex_in_convex_polygon(int_pts, num_of_inter):def _cmp(pt, center):vx = pt[0] - center[0]vy = pt[1] - center[1]d = math.sqrt(vx * vx + vy * vy)vx /= dvy /= dif vy < 0:vx = -2 - vxreturn vxif num_of_inter > 0:center = [0, 0]for i in range(num_of_inter):center[0] += int_pts[i][0]center[1] += int_pts[i][1]center[0] /= num_of_intercenter[1] /= num_of_interint_pts.sort(key=lambda x: _cmp(x, center))def area(int_pts, num_of_inter):def _trangle_area(a, b, c):return ((a[0] - c[0]) * (b[1] - c[1]) - (a[1] - c[1]) *(b[0] - c[0])) / 2.0area_val = 0.0for i in range(num_of_inter - 2):area_val += abs(_trangle_area(int_pts[0], int_pts[i + 1],int_pts[i + 2]))return area_valif __name__ == '__main__':rbbox1 = [0, 0, 2, 4, 0]rbbox2 = [0, 0, 4, 2, 0]corners1 = rbbox_to_corners(rbbox1)corners2 = rbbox_to_corners(rbbox2)pts, num_pts = [], 0for i in range(4):point = [corners1[2 * i], corners1[2 * i + 1]]if point_in_quadrilateral(point[0], point[1],corners2):num_pts += 1pts.append(point)for i in range(4):point = [corners2[2 * i], corners2[2 * i + 1]]if point_in_quadrilateral(point[0], point[1],corners1):num_pts += 1pts.append(point)for i in range(4):for j in range(4):ret, point = line_segment_intersection(corners1, corners2, i, j)if ret:num_pts += 1pts.append(point)sort_vertex_in_convex_polygon(pts, num_pts)polygon_area = area(pts, num_pts)print('area: {}'.format(polygon_area))

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！