图 —— 拓扑排序

当每个任务有前后置关系时，需要找到一种满足前后置关系的路线，将任务完成。

如果将每个任务看成一个节点，任务之间的前后置关系表示为有向图时，这种路线顺序叫做为图进行拓扑排序。也叫关键路径分析。

这里的图用邻接矩阵法表示，算法的关键是：

1. 找到一个没有后继的顶点 ；
2. 在图中删除它，放入结果数组中 ；
3. 重复 步骤 1 ，步骤 2 直到图中没有多余的节点；

代码：

/*** @ClassName Node* @Description 图节点* @Author lzq* @Date 2019/6/19 04:39* @Version 1.0**/
public class Node {public char label;  //存放的数据public boolean wasVisited;  //记录有无被访问过public Node(char label) {this.label = label;this.wasVisited = false;}
}

/*** @ClassName Graph3* @Description 拓扑排序* @Author lzq* @Date 2019/6/19 06:49* @Version 1.0**/
public class Graph3 {private final int MAX_VERTS = 20;  //表示一个图节点能连接的最大定点数private Node[] nodeList;  //顶点数组private int[][] adjMat; //邻接矩阵，用来存方节点之间关系的private int nNode;  //当前顶点数量private char[] sorteArray;  //存放拓扑排序之后字符数组public Graph3() {nodeList = new Node[MAX_VERTS];adjMat = new int[MAX_VERTS][MAX_VERTS];nNode = 0;for (int i = 0; i < MAX_VERTS; i++) {for (int j = 0; j < MAX_VERTS; j++) {adjMat[i][j] = 0;}}sorteArray = new char[MAX_VERTS];}/*** 添加节点* @param lab*/public void addNode(char lab) {nodeList[nNode++] = new Node(lab);}/*** 添加边* @param start* @param end*/public void addEdge(int start,int end) {adjMat[start][end] = 1;}/* *//*** 打印顶点* @param v*//*public void show(int v) {System.out.print(nodeList[v].label+"\t");}*//*** 拓扑排序*/public void topo() {int o = nNode;while (nNode > 0) {  //把所有顶点从图里面删除int c = noSuccessors();if(c == -1) {  //找不到没有后继顶点的顶点System.out.println("错误!!!");return;}sorteArray[nNode-1] = nodeList[c].label;deleteNode(c);  //从图中删除当前顶点}System.out.print("拓扑排序：");for (int i = 0; i < o; i++) {System.out.print(sorteArray[i]);}}private void deleteNode(int del) {if(del != nNode-1){   //要删除的顶点不是最后一个，就要处理邻接矩阵for (int i = del; i < nNode-1; i++) {  //删除顶点后面元素向前移动nodeList[i] = nodeList[i+1];}for (int i = del; i < nNode-1; i++) { //把邻接矩阵中，删除后面的行向上移动moveRowUp(i,nNode);}for (int col = del; col < nNode-1; col++) {moveColLeft(col,nNode-1);}}nNode--; //数量递减}/*** 矩阵行向上移* @param row* @param length*/private void moveRowUp(int row,int length) {for (int i = 0; i < length; i++) {adjMat[row][i] = adjMat[row+1][i];}}/*** 列往左移* @param col* @param length*/private void moveColLeft(int col,int length) {for (int row = 0; row < length; row++) {adjMat[row][col] = adjMat[row][col+1];}}/*** 查找途中没有后继顶点的顶点* @return*/private int noSuccessors() {boolean flag = true;for (int i = 0; i < nNode; i++) {flag = false;for (int j = 0; j < nNode; j++) {if (adjMat[i][j] > 0) {flag = true;break;}}if(!flag) {return i;}}return -1;}
}

/*** @ClassName TestDemo1* @Description 拓扑排序测试* @Author lzq* @Date 2019/6/19 07:21* @Version 1.0**/
public class TestDemo1 {public static void main(String[] args) {Graph3 graph3 = new Graph3();graph3.addNode('A');graph3.addNode('B');graph3.addNode('C');graph3.addNode('D');graph3.addNode('E');graph3.addNode('F');graph3.addNode('G');graph3.addNode('H');graph3.addEdge(0,3);graph3.addEdge(0,4);graph3.addEdge(1,4);graph3.addEdge(2,5);graph3.addEdge(3,6);graph3.addEdge(4,6);graph3.addEdge(5,7);graph3.addEdge(6,7);graph3.topo();}
}

测试代码表示的图：

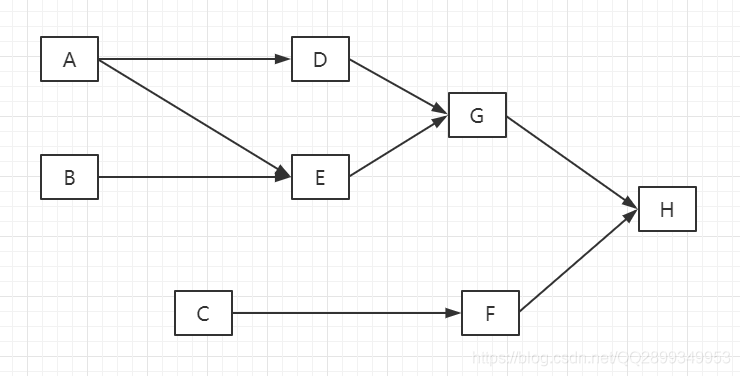
运行结果：

拓扑排序：BAEDGCFH

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！