糖尿病风险分析及预测
题目背景及要求
糖尿病是一种代谢性疾病,它的特征是患者的血糖长期高于标准值,当胰腺产生不了足够的胰岛素或者人体无法有效地利用所产生的胰岛素时,就会出现糖尿病。血糖正常值是指人空腹的时候血糖值在3.9~6.1毫摩尔/升,但是作为判断是否有高血糖,般是对人体进行两次重复测量,血糖值大于6.7毫摩尔/升即可诊断为糖尿病。临床表现为频尿、突易口渴、容易饥饿。同时伴随并发症。心血管疾病、非酮症之超渗透压的昏迷、糖尿病酮症酸中毒、中风、慢性肾脏病、足部溃疡等。目前糖尿病种类主要分为:型糖尿病、2型糖尿病、妊娠糖尿病和其他类型糖尿病。
附件1~2分别给出了有血糖值的检测数据和无血糖值的检测数据,文件数据的部分特征名已做脱敏处理,包含年龄、性别、各项体检数据等42个监测指标(详见表1),包含数值型、字符型、日期型等数据类型。请你们团队根据实际和附件中的数据信息,通过建立数学模型研究主要解决下列问题:
1.结合附件1的检测数据信息,对样本数据进行预处理,并作检测指标的统计分析,并解释数据揭示的规律性。
2.在问题 1 的基础上,通过降维的方法从 42 个检测指标中筛选出主要变量指标2使之尽可能具有代表性,并请详细说明建模主要变量的筛选过程及其合理性。
3.在问题2 基础上,采用上述样本和建模的主要变量,通过数据挖掘技术建立血3糖值预测模型,并进行模型验证。
4.在问题3 基础上,利用该模型对附件 2 的检测数据的血糖值进行预测,并对糖尿病风险进行说明。
数据预处理
1、数据观察及人工处理
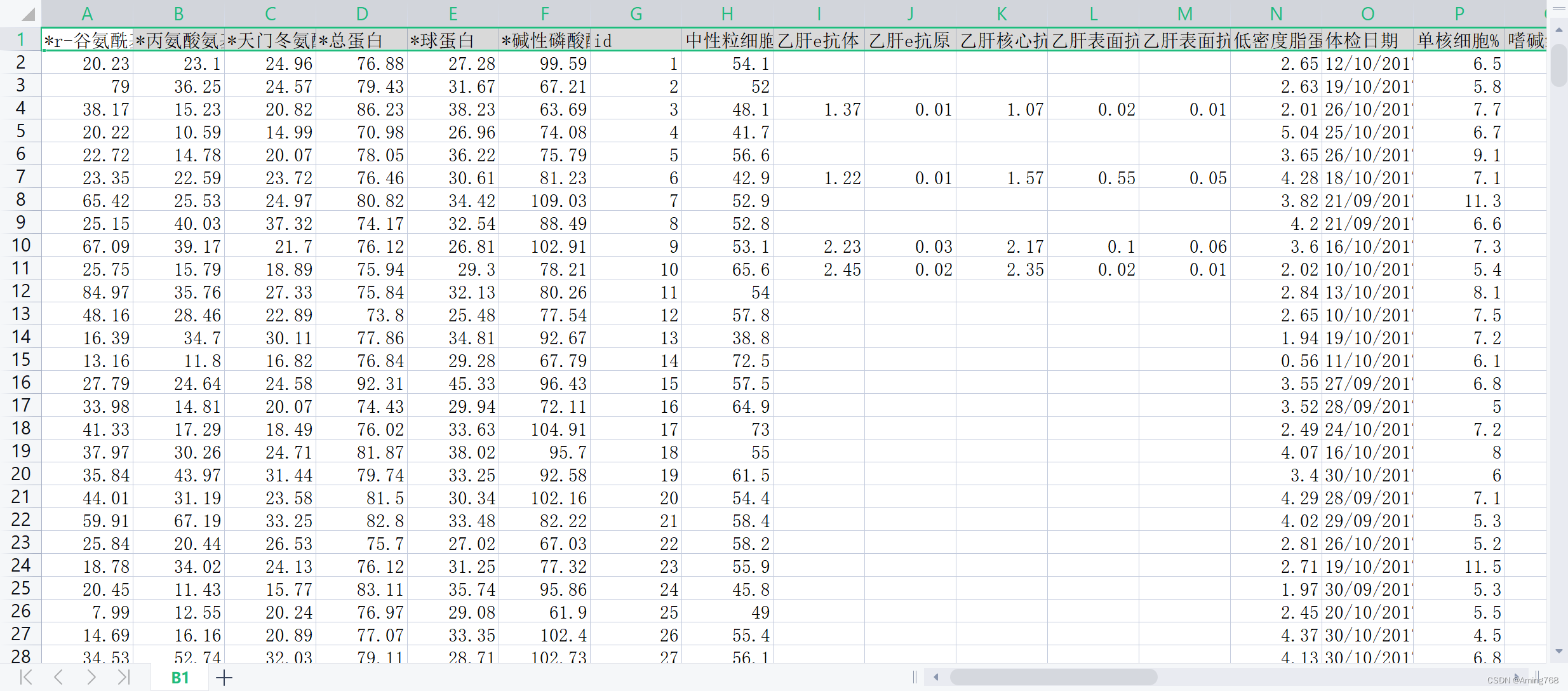
图1 附件一部分数据值一览表
附件一包含的特征值:*r-谷氨酰基转换酶 *丙氨酸氨基转换酶 *天门冬氨酸氨基转换酶 *总蛋白 *球蛋白 *碱性磷酸酶 id 中性粒细胞% 乙肝e抗体 乙肝e抗原 乙肝核心抗体 乙肝表面抗体 乙肝表面抗原 低密度脂蛋白胆固醇 体检日期 单核细胞% 嗜碱细胞% 嗜酸细胞% 尿素 尿酸 年龄 性别 总胆固醇 淋巴细胞% 甘油三酯 白球比例 白细胞计数 白蛋白 红细胞体积分布宽度 红细胞压积 红细胞平均体积 红细胞平均血红蛋白浓度 红细胞平均血红蛋白量 红细胞计数 肌酐 血小板体积分布宽度 血小板平均体积 血小板比积 血小板计数 血糖 血红蛋白 高密度脂蛋白胆固醇
(共42项)
1、其中,体检日期和id两项对血糖值明显无影响,可删去。
2、手动将数据集中“男”改为1,“女”改为0。
3、为便于后续数据处理,将带有百分号的数据特征化为绝对值,
例如,查询资料得
淋巴细胞%=淋巴细胞计数 / 白细胞计数 *100%
将“淋巴细胞%”一列化为“淋巴细胞计数%”,
其他含%的数据同理处理。
4、查资料发现有三个比值(中性粒细胞绝对值 / 淋巴细胞绝对值( NLR )、 血小板 / 淋巴细胞比值 ( PLR )、单核细胞 / 淋巴细胞比值( MLR ))与糖尿病的发生有较强关系,且能通过给定的数 据计算得出,故将其加入到数据集中。2、计算缺失值占比
数据导入:
import pandas as pd
import numpy as np
data = pd.read_csv("Path", encoding='ANSI')计算缺失值得:
| 乙肝e抗原 | 76.07% |
| 乙肝e抗体 | 76.07% |
| 乙肝表面抗原 | 76.07% |
| 乙肝表面抗体 | 76.07% |
| 乙肝核心抗体 | 76.07% |
从表格可知,乙肝五项缺失过多,直接删除。
3、补缺失值
用随机森林算法,将目标按缺失值占比从小到大排序,依次填充。
4、异常值处理
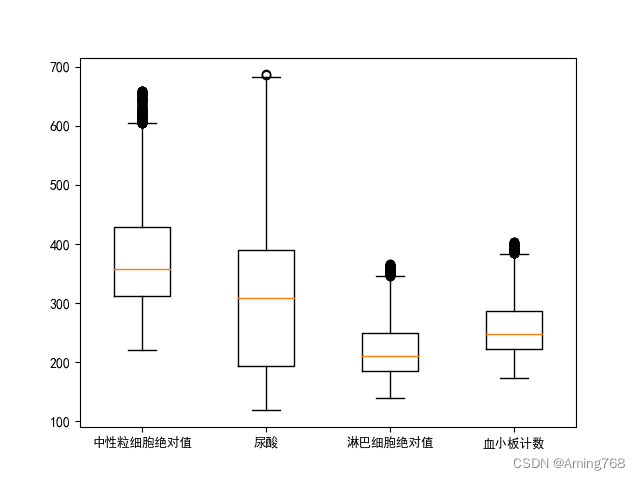
选择用箱线图处理异常值。
箱线图绘制实例:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
from pylab import mplmpl.rcParams['font.sans-serif'] = ['SimHei'] #黑体
mpl.rcParams['axes.unicode_minus'] = False
data = pd.read_csv("Path",engine='python',encoding='ANSI',usecols=[4, 5, 6, 7]) # 需要画箱型图的数据列
print(data.columns)
# 绘制箱型图
#用matplotlib来画出箱型图
plt.boxplot(x=data.values, labels=data.columns,whis=1.5) #columns列索引,values所有数值
plt.xticks(fontsize=9, rotation=0)plt.show()
运行结果实例:
数据分析
通过数据可视化分析数据揭示的规律性
1、频率分布直方图
import numpy as np
from sklearn import datasets
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import statsmodels.api as sm
from pylab import mpl
from scipy import stats
import matplotlib.pylab as plt
import seaborn as snsmpl.rcParams['font.sans-serif'] = ['SimHei'] # 黑体
mpl.rcParams['axes.unicode_minus'] = False
data = pd.read_csv("Path", encoding='ANSI')
# 直方图与概率图
train_lable = data['年龄']
sns.distplot(train_lable) # 直方图(单变量分布图)
plt.show()运行结果实例:
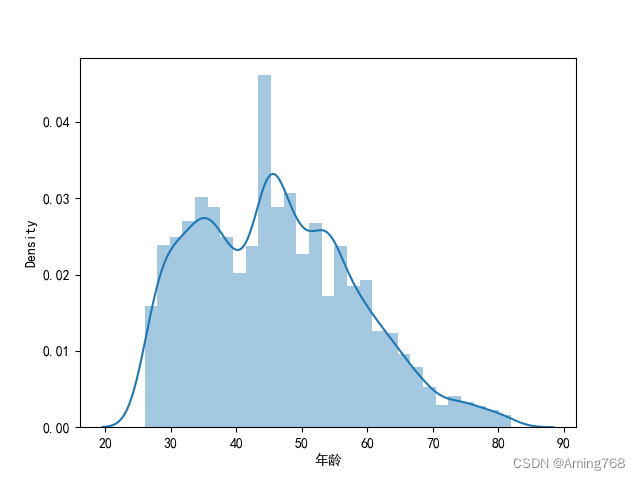
2、散点图
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
from pylab import mplmpl.rcParams['font.sans-serif'] = ['SimHei'] #黑体
mpl.rcParams['axes.unicode_minus'] = False
data = pd.read_csv("Path", engine='python', encoding='ANSI')
# 绘制散点图
plt.figure(figsize=(6, 6)) # 图片像素大小
plt.scatter(data['id'], data['血糖'], color="blue") # 散点图绘制
plt.xlabel('id')
plt.ylabel('血糖')
plt.grid() # 显示网格线
plt.title('血糖值散点图')
plt.show() # 显示图片
运行结果实例:
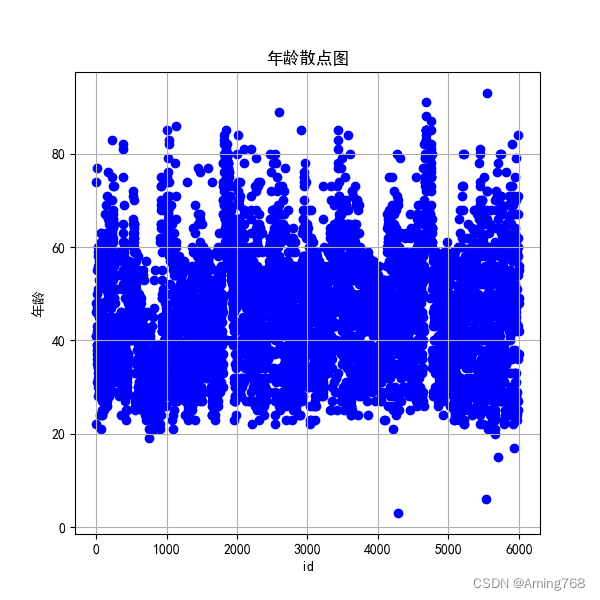
3、密度分布图
注意:血糖值大于6.1定义为糖尿病,分为两个文件对比患病率
import numpy as np
from sklearn import datasets
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import statsmodels.api as sm
from pylab import mpl
from scipy import stats
import matplotlib.pylab as plt
import seaborn as snsmpl.rcParams['font.sans-serif'] = ['SimHei'] # 黑体
mpl.rcParams['axes.unicode_minus'] = False
data0 = pd.read_csv("Path0", encoding='ANSI')
data1 = pd.read_csv("Path1", encoding='ANSI')
# 绘制多个变量的密度分布图
# plotting both distibutions on the same figure
for col in data1.columns:dt = data1[col]fig0 = sns.kdeplot(data0[col], shade=True, color="r", label='健康')fig0.legend(loc='upper right')fig1 = sns.kdeplot(data1[col], shade=True, color="b", label='患病')fig1.legend(loc='upper right')plt.title(col + '指标与糖尿病患病率')plt.show()运行结果实例:
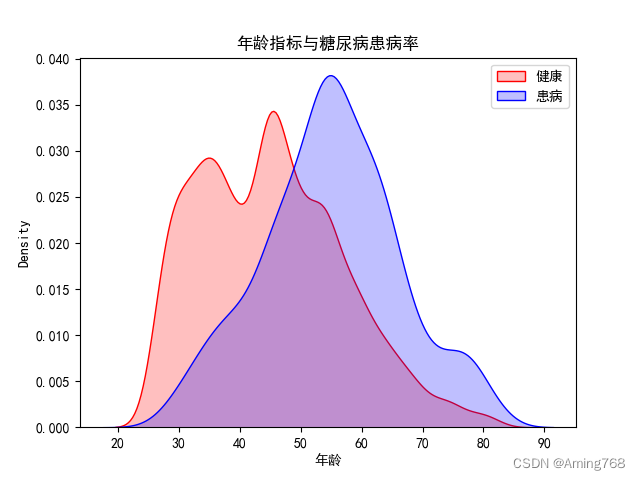
综合以上三种可视化方式可看出,糖尿病患病风险与随年龄增长而增大。
其他数据项分析同上。
4、相关性热力图
# 画热力图data_corr = data.corr()
# print(data_corr)
fig = plt.figure(figsize=(10, 8))
ax = sns.heatmap(data_corr,vmax=0.9,square=True,cbar=True,annot=True,fmt='.2f',annot_kws={'size': 4})
ax.tick_params(labelsize=7)
# 旋转x轴刻度上文字方向
ax.set_xticklabels(ax.get_xticklabels(), rotation=90)
ax.set_yticklabels(ax.get_yticklabels(), rotation=0)运行结果实例:
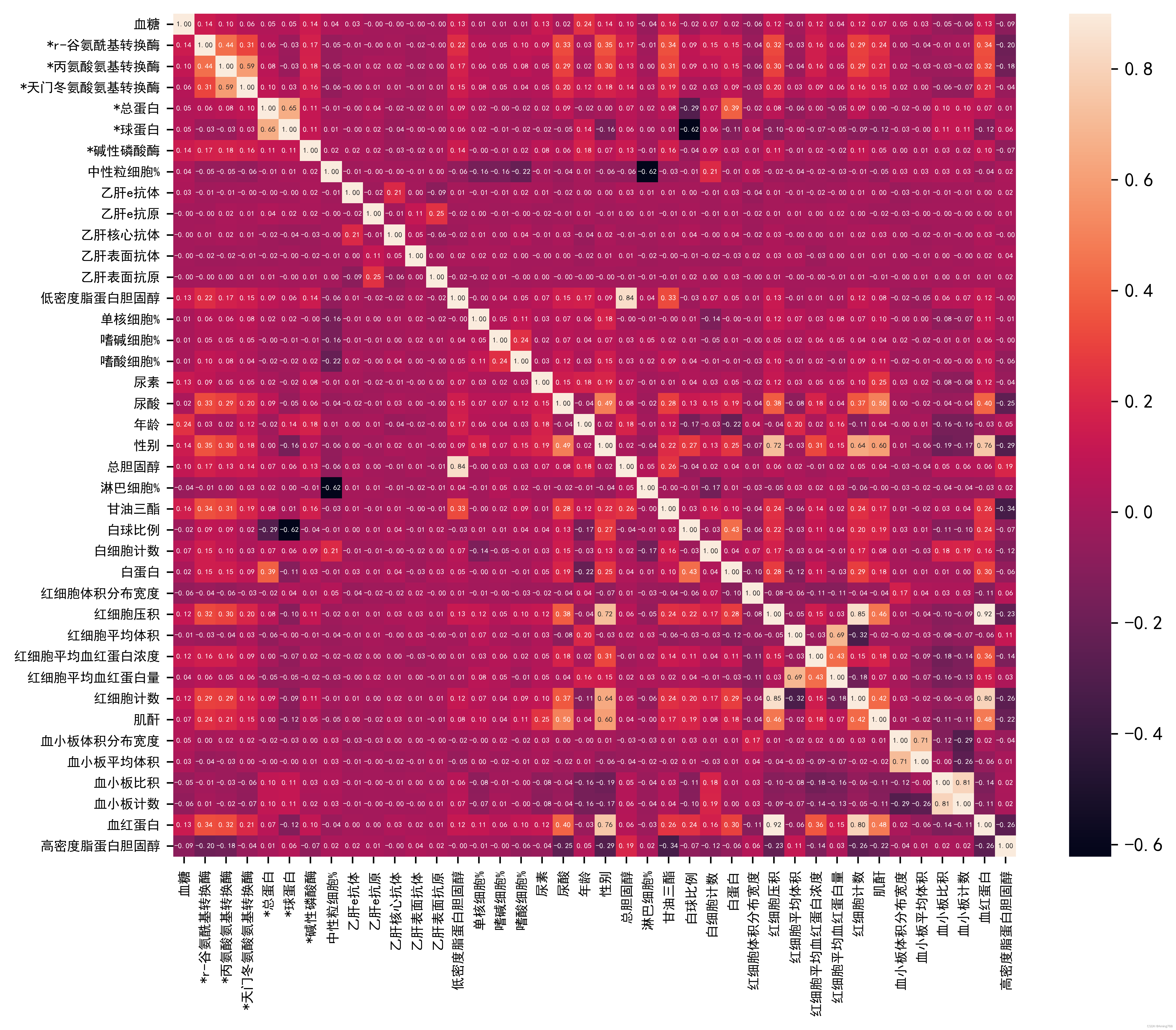
绝对值越接近1,两数据项相关性越强。
5、饼状图
主要用于分析各数据项占比,这里省略。
筛选主要变量
1、LightGBM算法
LightGBM 算法是一种基于树模型的梯度提升算法,适用于本题的回归问题。它通过集成多个树模型来逐步提升整体预测性能,能将所有特征的评分进行标准化,得出各特征的相对重要性排名。 实例: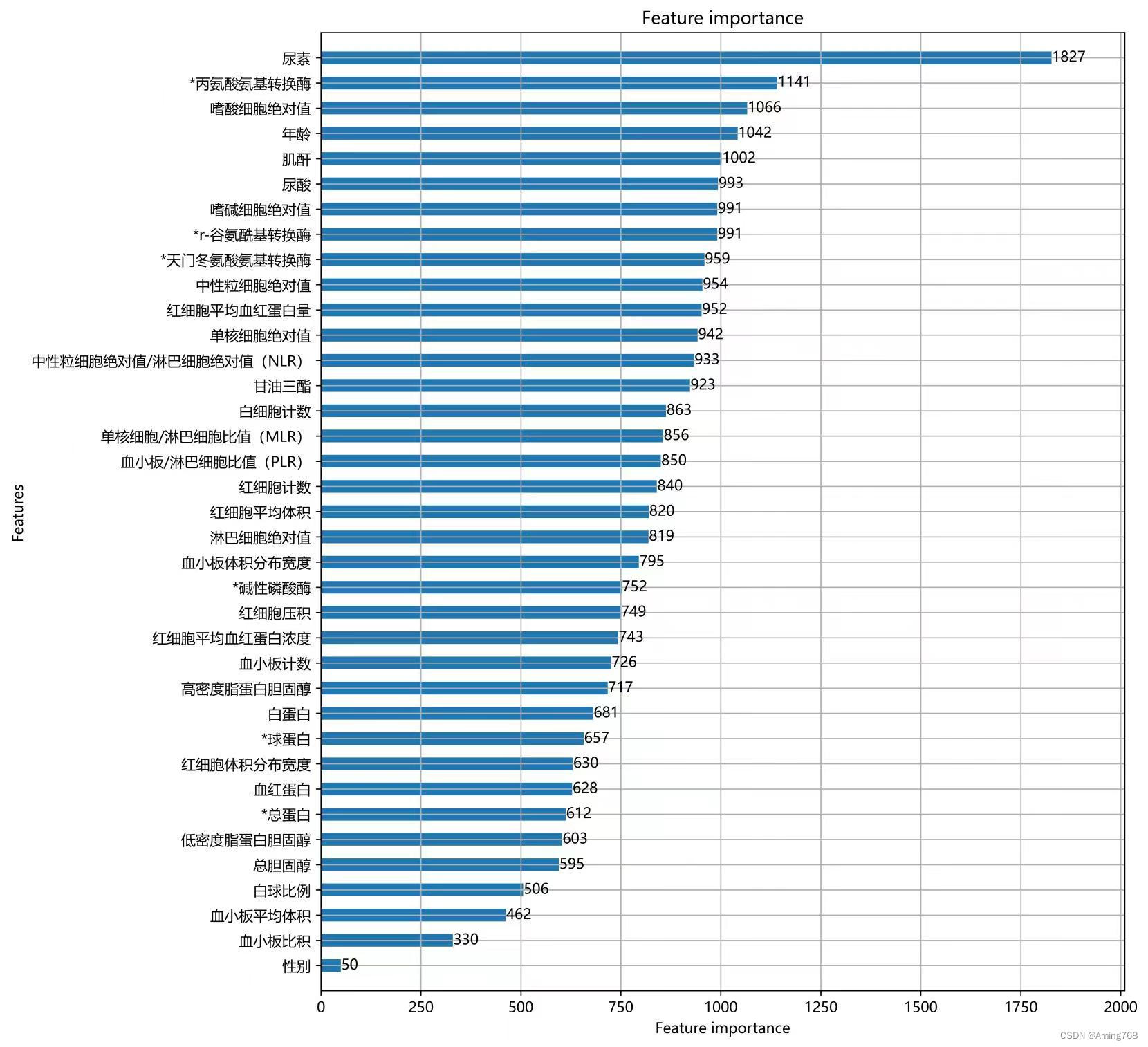
将重要性小于阈值的特征视为不重要特征,删除。
2、相关性分析
利用数据分析中的热力图,具有较高相关性的特征只留下与血糖值关系更密切的一个,防止出现多重共线性。
模型构建
1、评价指标介绍
平均绝对误差( MAE )为预测值和真实值绝对误差的平均值,可用于反映预测的准确 性和误差大小; 平均绝对百分比误差( MAPE )在 MAE 的基础上,不仅考虑预测值和真实值之间的偏 差,还考虑到 偏差和真实值之间的比例; 均方误差( MSE )可放大预测偏差较大的值,用于比较不同预测模型的稳定性; 均方根误差( RMSE )在 MSE 的基础上做平方根 , 能够保证量纲不发生变化。相关系数 R 判断拟合效果
2、多重线性回归模型
data = pd.read_csv("Path", encoding='utf-8', nrows=300)
cols = ['尿素', '年龄', '甘油三酯', '红细胞计数'] # 主要变量,这里只是举例def looper(limit):for i in range(len(cols)):data1 = data[cols]x = sm.add_constant(data1) # 生成自变量y = data['血糖'] # 生成因变量model = sm.OLS(y, x) # 生成模型result = model.fit() # 模型拟合pvalues = result.pvaluespvalues.drop('const', inplace=True) # 把const取得pmax = max(pvalues) # 选出最大的P值if pmax > limit:ind = pvalues.idxmax() # 找出最大P值的indexcols.remove(ind) # 把这个index从cols中删除else:return resultresult = looper(0.05)
print(result.summary())
根据结果拟合出方程,再用评价指标进行评价。
该方法拟合效果一般,可作为对照组
3、XGBoost回归预测
# 提取特征和目标列
y = df['血糖'].values
df = df.drop('血糖', axis=1)
x = df.values
X_train, X_validation, y_train, y_validation = train_test_split(x, y, test_size=0.025, random_state=42)# 建模,用贝叶斯优化寻找出的最佳的建模参数
xgb_model = xgb.XGBRegressor(max_depth=3,learning_rate=0.03,n_estimators=2000,subsample=0.8,reg_lambda=1,reg_alpha=100,min_child_weight=5,# max_depth=2,gamma=0.3,colsample_bytree=0.7,objective='reg:squarederror',booster='gbtree',random_state=0)# 拟合
bst = xgb_model.fit(X_train, y_train)
y_validation_pred = xgb_model.predict(X_validation) # 预测
bst.save_model('test.model.txt')
print(bst)# 画图
plt.figure(figsize=(14, 7))
plt.plot(range(y_validation.shape[0]),y_validation,color="blue",linewidth=1.5,linestyle="-")
plt.plot(range(y_validation_pred.shape[0]),y_validation_pred,color="red",linewidth=1.5,linestyle="-.")
plt.legend(['真实值', '预测值'])
plt.title("真实值与预测值比对图")
plt.show() #显示图片
注意:其中的参数需要不断进行贝叶斯优化以及人工调参,得到最优参数
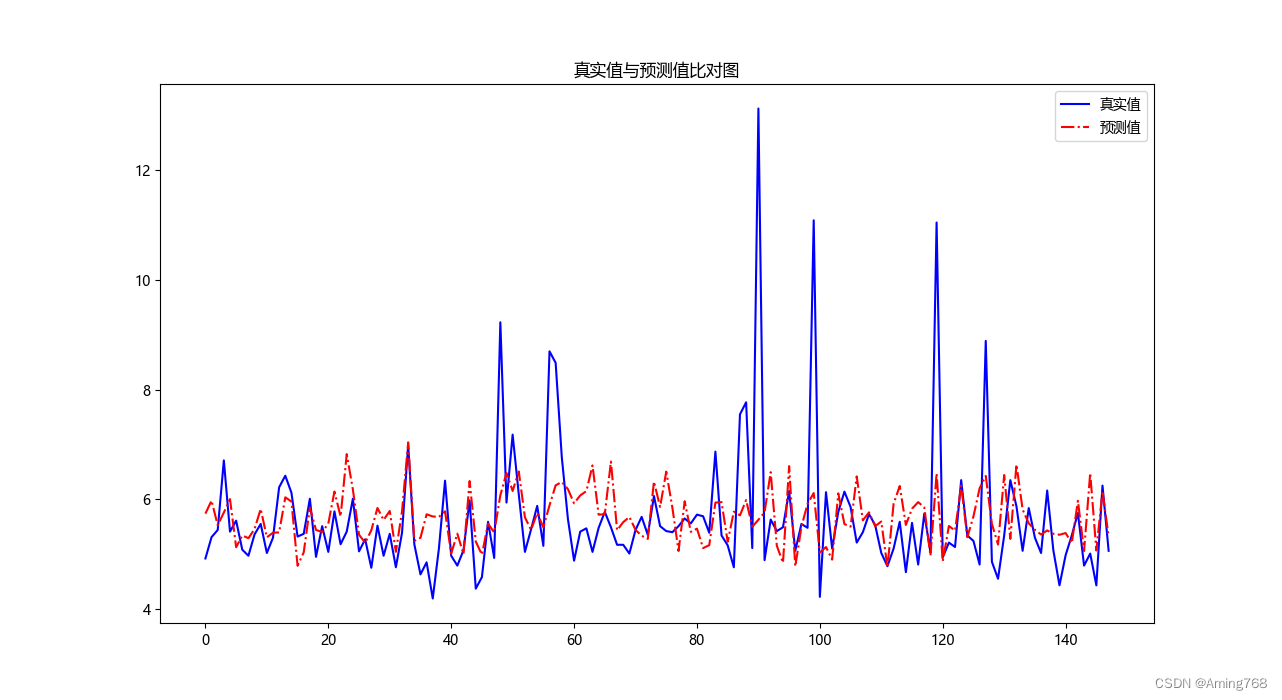
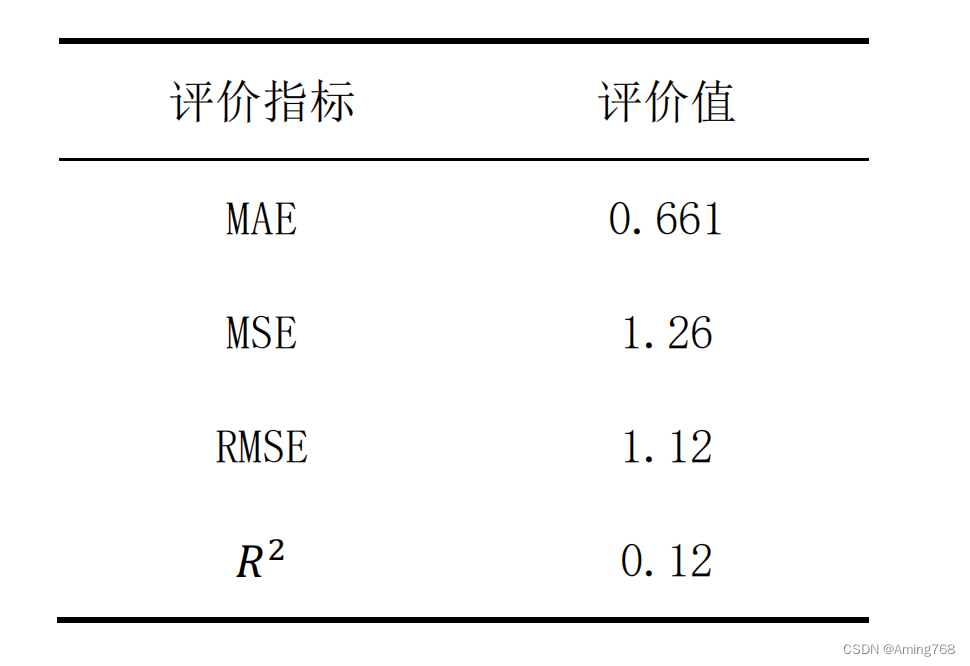
由图像和评价指标可得,该方法比多重线性回归模型有了较大提高,但对于高血糖值的预测效果较差。
4、随机森林分类回归模型
主要思想:将数据集分为高血糖组和低血糖组。将高血糖组、低血糖组的数据分别用于训练高血糖预测模型和低血糖预测模型。对于最终的测试集,依据分类预测结果决定使用高血糖模型预测结果还是低血糖模型预测结果。
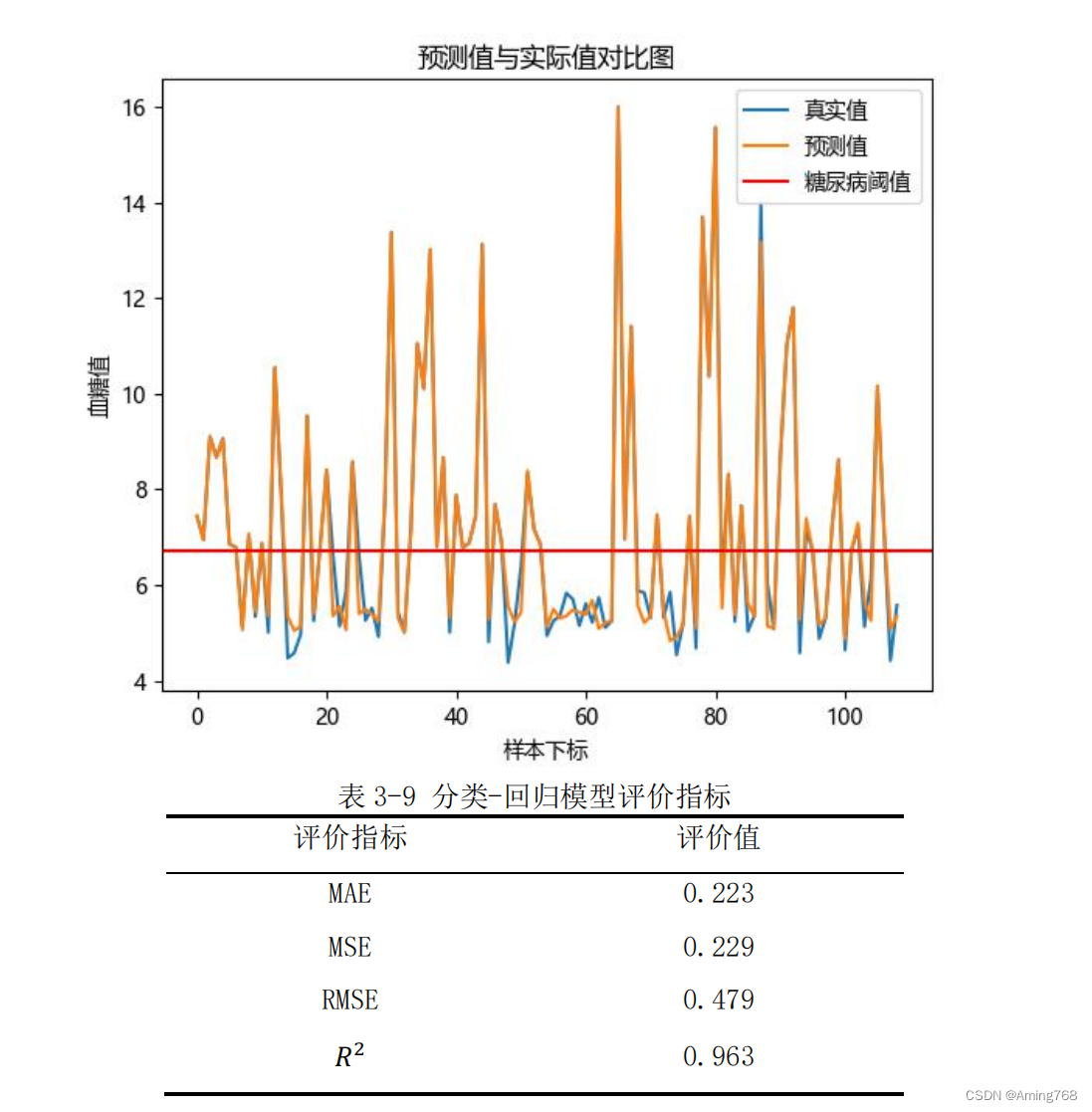
由图像和评价指标可得,该模型效果非常好,显著提高了预测正确率。
将此模型作为最终模型。
缺点
1、对于附件二中需要预测的数据预测效果不佳,特别是高血糖类型。
2、实际调参中使用贝叶斯优化时过于粗糙,所得“最优参数”与实际最优参数应该存在较大差距。
后记
如有问题,恳请各位能提出批评建议,不胜感激。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!