Proof (of knowledge) of exponentiation

1. Proof of exponentiation

Proof of exponentiation是基于adaptive root assumption（充分必要条件）的。


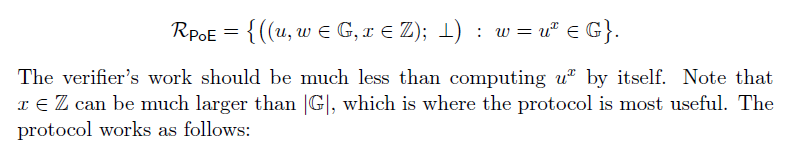
特别适合当$x$很大时，计算 r = x m o d l , u r r=x\ mod\ l,\ u^r r=x mod l, ur将大量节约verifier直接计算 u x u^x ux的时间。

借助Fiat-Shamir heuristic，可将上面的交互式PoE转化为NI-PoE：

对应在https://github.com/dignifiedquire/rust-accumulators/blob/master/src/proofs.rs中的实现为：

/// NI-PoE Prove
/// Assumes `u^x = w`
/// All operations are `mod n`.
pub fn ni_poe_prove(x: &BigUint, u: &BigUint, w: &BigUint, n: &BigUint) -> ExponentProof {debug_assert!(&u.modpow(x, n) == w, "invalid input");// l <- H_prime(x, u, w)let mut to_hash = x.to_bytes_be();to_hash.extend(&u.to_bytes_be());to_hash.extend(&w.to_bytes_be());let l = hash_prime::<_, Blake2b>(&to_hash);// q <- floor(x/l)let q = x.div_floor(&l);//Prover sends Q <- u^q ∈ G to the Verifier.u.modpow(&q, n)
}/// NI-PoE Verify
/// Assumes `u^x = w`
/// All operations are `mod n`.
pub fn ni_poe_verify(x: &BigUint,u: &BigUint,w: &BigUint,q: &ExponentProof,n: &BigUint,
) -> bool {// l <- H_prime(x, u, w)let mut to_hash = x.to_bytes_be();to_hash.extend(&u.to_bytes_be());to_hash.extend(&w.to_bytes_be());let l = hash_prime::<_, Blake2b>(&to_hash);// r <- x mod llet r = x.mod_floor(&l);// Q^l u^r == w&((q.modpow(&l, &n) * &u.modpow(&r, &n)) % n) == w
}// 基于hash值来获取prime数值。
// When the proofs are made non-interactive, using the
// Fiat-Shamir heuristic the challenge is generated by hashing the previous transcript/// Hash the given numbers to a prime number.
/// Currently uses only 128bits.
pub fn hash_prime, D: Digest>(input: &[u8]) -> BigUint {let mut y = BigUint::from_bytes_be(&D::digest(input)[..16]);while !probably_prime(&y, 20) {y = BigUint::from_bytes_be(&D::digest(&y.to_bytes_be())[..16]);}y
}

2. Proof of knowledge of exponentiation

2.1 有安全攻击隐患的PoKE

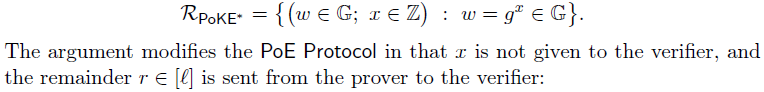
此时，verifier不需要自己计算余数$r$，改由prover提供。同时注意，此时要求discrete logarithm base $g$必须被包含在CRS中$\Rightarrow$ 存在安全攻击问题，不是secure protocol：

2.2 基于base $g$和$u$的两次PoKE

对witness $x$的证明，做了两次PoKE证明，一次是base $g$，一次是base $u$。

以上，proof中包含了两个group元素 Q 和 Q ′ Q和Q' Q和Q′。如下，通过增加一个challenge $\alpha$，可以将proof中的group元素仍然减为1个$Q$：

借助Fiat-Shamir heuristic，可将上面的交互式PoKE2转化为NI-PoKE2：

对应在https://github.com/dignifiedquire/rust-accumulators/blob/master/src/proofs.rs中的实现为：

//proof of knowledge of exponent, i.e. a proof that a computationally bounded prover knows the discrete logarithm between two elements in a group of unknown order. The proof is succinct in that the proof size and verification time is independent of the size of the discrete-log./// NI-PoKE2 Prove
/// assumes `u^x = w`
/// All operations are `mod n`.
pub fn ni_poke2_prove(x: impl Into,u: &BigUint,w: &BigUint,n: &BigUint,
) -> (BigUint, BigUint, BigInt) {let x: BigInt = x.into();debug_assert!(&modpow_uint_int(u, &x, n).unwrap() == w, "invalid input");// g <- H_G(u, w)let mut to_hash = u.to_bytes_be();to_hash.extend(&w.to_bytes_be());let g = hash_group::<_, Blake2b>(&to_hash, n);// z = g^xlet z = modpow_uint_int(&g, &x, n).expect("invalid state");// l <- H_prime(u, w, z)to_hash.extend(&z.to_bytes_be());let l: BigInt = hash_prime::<_, Blake2b>(&to_hash).into();// alpha = H(u, w, z, l)to_hash.extend(&l.to_bytes_be().1);let alpha = BigUint::from_bytes_be(&Blake2b::digest(&to_hash)[..]);// q <- floor(x/l)// r <- x % llet (q, r) = x.div_rem(&l);// Q <- (ug^alpha)^qlet q_big = modpow_uint_int(&(u * &g.modpow(&alpha, n)), &q, n).expect("invalid state");(z, q_big, r)
}/// NI-PoKE2 Verify
/// assumes `u^x = w`
/// All operations are `mod n`
pub fn ni_poke2_verify(u: &BigUint,w: &BigUint,pi: &(BigUint, BigUint, BigInt),n: &BigUint,
) -> bool {// {z, Q, r} <- pilet (z, q_big, r) = pi;// g <- H_G(u, w)let mut to_hash = u.to_bytes_be();to_hash.extend(&w.to_bytes_be());let g = hash_group::<_, Blake2b>(&to_hash, n);// l <- H_prime(u, w, z)to_hash.extend(&z.to_bytes_be());let l = hash_prime::<_, Blake2b>(&to_hash);// alpha = H(u, w, z, l)to_hash.extend(&l.to_bytes_be());let alpha = BigUint::from_bytes_be(&Blake2b::digest(&to_hash)[..]);// Q^l(ug^alpha)^rlet lhs: BigInt = ((q_big.modpow(&l, n)* modpow_uint_int(&(u * &g.modpow(&alpha, n)), &r, n).expect("invalid state"))% n).into();// wz^alphalet z_alpha = z.modpow(&alpha, n);let rhs: BigInt = ((w * z_alpha) % n).into();lhs == rhs
}

3. Aggreating Knowledge of Co-prime Roots

在第2节中，已可证明 u x = w u^x=w ux=w，若有一系列的co-prime roots x 1 , . . . , x n x_1,...,x_n x1​,...,xn​满足 w i x i = α i w_i^{x_i}=\alpha_i wixi​​=αi​且 g c d ( x i , x j ) = 1 ∀ i , j ∈ [ 1 , n ] , i ! = j gcd(x_i,x_j)=1\forall i,j\in[1,n],i!=j gcd(xi​,xj​)=1∀i,j∈[1,n],i!=j


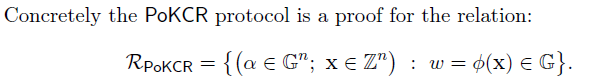
https://github.com/cambrian/accumulator/中也有相应的代码实现，且实现的性能要优于https://github.com/dignifiedquire/rust-accumulators/。
``

#[allow(non_snake_case)]
#[derive(PartialEq, Eq, Hash, Clone, Debug)]
/// Struct for NI-PoKCR.
pub struct Pokcr {w: G::Elem,
}impl Pokcr {/// Generates an NI-PoKCR proof.pub fn prove(witnesses: &[G::Elem]) -> Self {Self {w: witnesses.iter().fold(G::id(), |a, b| G::op(&a, b)),}}/// Verifies an NI-PoKCR proof.pub fn verify(alphas: &[G::Elem], x: &[Integer], proof: &Self) -> bool {let y = multi_exp::(alphas, x);let lhs = G::exp(&proof.w, &x.iter().product());lhs == y}
}

参考资料：
[1] 2018年论文《Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains》
[2] 博客密码学中的各种假设——DL/SDH…

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！