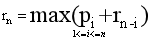钢条切割问题——递归求解法
这道题在算法导论(第三版)的204页
钢条切割问题是这样的:
给定一段长度为n英寸的钢条和一个价格表pi(i=1,2,...,n),求切割钢条方案,使得销售收益rn最大。注意,如果长度为n英寸的钢条的价格pn足够大,最优解可能就是完全不需要切割。
假设有一张价格表为:
| 长度i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 价格pi | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
基本思路:我们将钢条从左边切割下长度为i的一段,只对右边剩下的长度为n-i的一段继续进行切割(递归求解),对左边的一段则不再进行切割。则可得公式:
其中pi为左边长度为i的钢条的收益,rn-i为右边长度为n-i的钢条继续切割后得到的最优收益,rn为长度为n的钢条切割后得到的最优收益。
递归实现代码如下:
package dynamic;/** 钢条切割 算法导论P204*/
public class Steel {/*** 比较大小* @param a* @param b* @return*/public static int max(int a, int b) {return (a > b ? a : b);}/*** * @param p 存储价格的数组,p从0开始存储* @param n 钢条长度为n* @return 返回长度为n的钢条切割后得到的最大收益*/public static int cut(int[] p,int n){//如果长度为0,则0收益if(n==0)return 0;int q = -1;// 思路://将长度为n的钢条从左切割长度为i的一段,则右端为长度为n-i的一段//其中长度为i的左端不继续切割,只继续切割右端的那一部分//一直递归的cut(p,n-i)最后得到的是长度为n-i的钢条切割后的最大收益for(int i = 0; i < n; i++) {q = max(q,p[i] + cut(p,n-i-1)); //切割后的收益和不切割}return q;}public static void main(String[] args) {int[] p = {1,5,8,9,10,17,17,20,24,30};int n = 4;System.out.println(cut(p,n));}}
因为这道题是用递归实现的,所以必然存在一个缺点,那就是当数据n很大时,方法cut会反复调用相同的参数值对自身进行递归调用,即它反复求解相同的子问题。这会导致cut方法运行时间为n的指数函数。效率很低!
所以我们需要进行优化,可以使用动态规划法来求解最优钢条切割问题。
如何利用动态规划法来求解最优钢条切割问题请见下文。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!