目录

• 一、策略学习
• 二、参考资料

一、策略学习

思路：用policy network来近似策略函数 $\pi$​ ，用policy gradient算法来训练这个网络

函数近似的一般方法：线性函数，kernel函数，神经网络（就叫policy network了）

softmax是用来做映射的，因为我们需要各个动作的概率，所以要求输出都为正数，且加和为1，这里的softmax就是让输出具有这样的特征。

我们要找到一种评价方式，在这种评价方式下，当前的局面是最好的。因此，我们肯定需要状态价值函数：

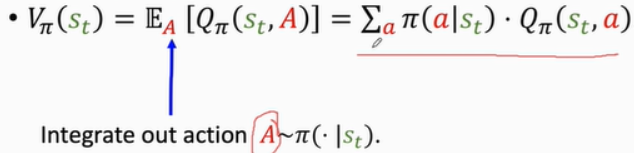
目标函数： J ( θ ) = E S [ V ( S ; θ ) ] J(\theta)=E_S[V(S;\theta)] J(θ)=ES​[V(S;θ)]，策略学习就是改进θ，让$J(\theta )$最大

策略梯度：如果a是离散的，那么

则有

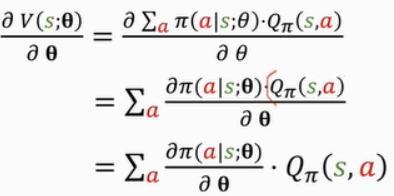
其中 Q π ( s , a ) Q_\pi(s,a) Qπ​(s,a)是与$\pi$有关的，而$\pi$是与θ有关的，但为了便于理解，把它看作是无关的，拎到外面。

但实际上一般不用这种方法算策略梯度，而是作这个策略梯度的蒙特卡洛近似：

这里的log只是一种方法，莫烦的说法是用log的收敛性比较好。

现在得到了两种策略梯度的计算形式。

1）用第一种形式：

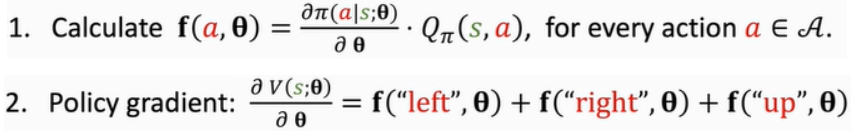
但因为是求和，所以只能用于动作空间是离散区间的情况

2）用第二种形式：适合动作空间是连续区间的情况（离散区间也可以用）

由于 a ^ \hat a a^是根据$\pi$抽样得到的，所以 g ( a ^ , θ ) g(\hat a,\theta) g(a^,θ)是对策略梯度的无偏估计。

流程总结：

这里第3步的 q t q_t qt​怎么算？

1）reinforce方法：用 u t u_t ut​来近似代替 U t U_t Ut​

缺点：需要玩完一局，才能知道 u t u_t ut​，才能更新一次

2）actor-critic方法：用神经网络做函数近似

以后再说。

二、参考资料

深度强化学习（全）

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！