实验一 初等模型
实验目的:
1. 掌握初等模型建模的基本思路和方法;
2. 掌握多种模型优劣的基本评判标准;
3. 掌握最小二乘法原理。
实验原理:
1.利用随机函数来生成随机数,并进行随机模拟;
2.对数据进行可视化处理;
3.对数据进行线性拟合。

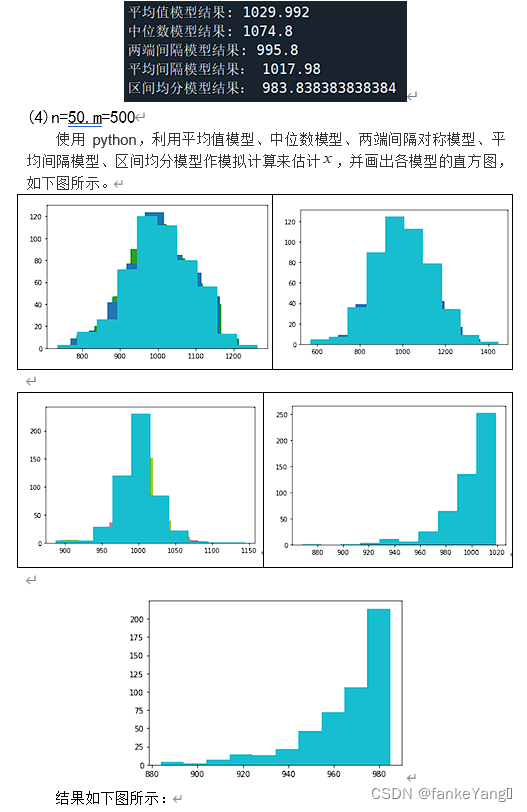
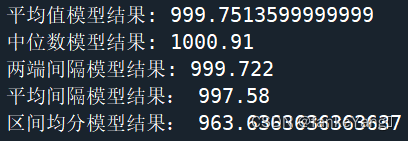
代码如下:
import random
import math
import numpy as np
def random_int_list(start, stop, length):
start, stop = (int(start), int(stop)) if start <= stop else (int(stop), int(start))
length = int(abs(length)) if length else 0
random_list = []
for i in range(length):
random_list.append(random.randint(start, stop))
return random_list
def huahua(x):
length = len(x)
print(length)
x.sort()
print(x)
if (length % 2)== 1:
z=length // 2
y = x[z]
else:
y = (x[length//2]+x[length//2-1])/2
return y
n=50;
m=500;
b=0;
c=0
d=0
e=[]
f=[]
g=[]
h=[]
j=[]
import matplotlib.pyplot as plt
plt.show()
#for i in range (n):
for i in range(m):
a = np.array(random_int_list(1, 1000,n ))
#print(np.mean(a))
b=b+np.mean(a)
#e=e+[np.mean(a)]
c=c+np.mean(huahua(a));
d=d+max(a)+min(a)-1
e=e+[np.mean(a*2-1)]
f=f+[np.mean(huahua(a*2-1))]
g=g+[max(a)+min(a)-1]
h=h+[(1+1/n)*max(a)-1]
j=j+[(1+1/(2*n-1))*(max(a)-1/2*n)]
plt.hist(e,bins=10)
plt.hist(f,bins=10)
plt.hist(g,bins=10)
#plt.hist(h,bins=10)
# plt.hist(j,bins=10)
# plt.title("data analyze")
# plt.xlabel("height")
# plt.ylabel("rate")
print("平均值模型结果:",(b/m)*2-1)
print("中位数模型结果:",(c/m)*2-1)
print("两端间隔模型结果:",d/m)
print("平均间隔模型结果:",(1+1/n)*max(a)-1)
print("区间均分模型结果:",(1+1/(2*n-1))*(max(a)-1/2*n))
第2题:
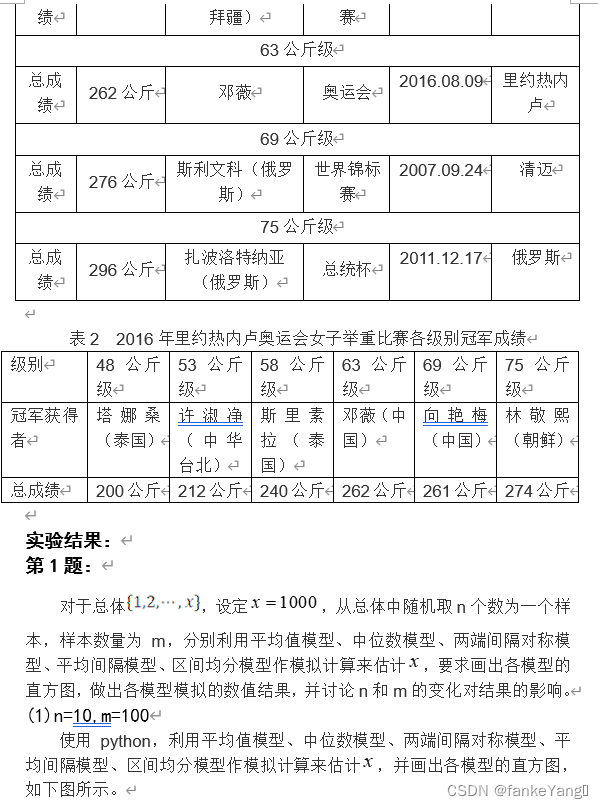
利用表1的女子举重比赛的世界纪录建立线性模型,并利用该模型对表2的各级别冠军进行排序。
使用Matlab对表一中的数据进行线性拟合,w值为公斤级,y值为总成绩。Matlab代码如下:
W=[48,53,58,63,69,75];
Y=[217,233,252,262,276,286];
p=polyfit(W,Y,1);
Y1=polyval(p,W);
plot(W,Y,'rx');
hold on;
plot(W,Y1,'b');
legend('原数据','线性模型')
运行结果如下图所示:

图 7 线性模型拟合图
根据所建立的线性模型得出如下表格:
表 1 成绩拟合表
| 公斤级(KG) | 拟合成绩(kg) |
| 48 | 221.1 |
| 53 | 233.9 |
| 58 | 246.7 |
| 63 | 259.5 |
| 69 | 274.8 |
| 75 | 290.2 |
根据表二,得出线性模型与2016年里约热内卢奥运会女子举重比赛各级别冠军成绩差距表。
表 2 成绩差值表
| 拟合成绩(kg) | 冠军成绩(kg) | 与拟合成绩差值(kg) |
| 221.1 | 200 | -21.1 |
| 233.9 | 212 | -21.9 |
| 246.7 | 240 | -6.7 |
| 259.5 | 262 | +2.5 |
| 274.8 | 261 | -13.8 |
| 290.2 | 274 | -16.2 |
根据上表得出冠军排名如下表所示:
表 3 冠军排名表
| 姓名 | 公斤级 | 成绩 | 排名 |
| 邓薇 | 63 | 262 | 1 |
| 斯里素拉 | 58 | 240 | 2 |
| 向艳梅 | 69 | 261 | 3 |
| 林敬熙 | 75 | 274 | 4 |
| 塔纳桑 | 48 | 200 | 5 |
| 许淑净 | 53 | 212 | 6 |
总结与思考:
针对第一题,当n值与m值逐渐变大,五个模型的结果越逼近1000.综合来看,平均间隔模型在五个模型中占优。当模拟时增加样本的大小n和样本的数量m,可以得到更加可信的结论。
针对第二题,使用线性模型可以快速得到拟合曲线,但使用线性模型仍有一定的误差。
通过本次实验,我不仅学会了使用MATLAB建立线性模型,也学会使用Python来产生随机数,并绘制直方图。同时也了解了平均值模型、中位数模型、两端间隔对称模型、平均间隔模型、区间均分模型进行估算的原理和操作,收获了许多。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!