文章目录

• 视觉算法知识荟萃
• • 视觉算法八股
  • • ToF相机和结构光相机
    • • 原理
      • 测量原理
      • 常见相机
    • 针孔相机模型
    • 激光雷达投影到 2D 平面
    • 多任务平衡
    • 自动驾驶检测模型对 corner case 进行的针对性优化
    • 密集行人场景遮挡
    • • 这种遮挡对跟踪的影响
    • 推导全连接层梯度回传
    • 为什么多卡训练时，GPU0显存要多一些
    • 手写卷积
    • • 卷积核的参数量
    • 结构风险和经验风险
    • Delta K
    • Abs Rel
    • RMSE
    • Silog
    • VNL
    • Gradient Loss
    • SoftMax
    • • SoftMax 反向传播
    • CrossEntropy
    • Dropout 原理
    • • Dropout 前向传播
      • Dropout 反向传播
    • SVM 原理
    • LR 逻辑回归
    • • 手写sigmoid
      • 为什么选择 sigmoid
      • sigmoid反向传播
    • Transformer
    • • QKV是如何出来的
      • Transformer为什么使用LN，不适用BN
    • Swin-Transformer
    • Adam，SGD
    • • Adam的创新点
      • 如何修改SGD
      • SGD 是否需要 shffule 数据集
      • SGD 解方程
    • NMS
    • • SoftNMS
    • IoU
    • 边缘检测算法
    • • Sobel
      • Laplacian
    • Pooling Layer
    • • 手写 Pooling Layer
      • Pooling Layer 传播方式
    • 手写 BN
    • • BN 层的作用
      • BN在训练和测试时的区别
      • BN如何加速
    • 过拟合
    • P范数
    • • 1范数
      • 2范数
    • 欠拟合
    • 训练出现NaN
  • 目标检测
  • • 两阶段检测模型
    • • R-CNN
      • Fast R-CNN
      • Faster R-CNN
      • • 优点
      • 缺点
      • Unsniffer
    • 单阶段检测模型
    • • YOLO
      • SSD (Single Shot multibox Detector)
      • • 优点
        • 缺点
  • 运动控制
  • • • PID
      • KCF
  • 单目深度估计
  • • SM4Depth
    • • SimMIM 预训练
      • PST
      • Bin-based Depth Estimation
      • 训练集
    • 轻量级单目深度估计
    • • CVPR 2022 WorkShop
      • DANet
  • 双目深度估计
  • • 视差转深度的公式推导
  • 轻量级平台配置
  • • TFLite 配置流程
    • TensorRT

视觉算法知识荟萃

视觉算法八股

ToF相机和结构光相机

原理

1. ToF相机：ToF相机通过发送短脉冲光源（通常是红外光）到场景中，然后测量光线从相机发送到物体表面并返回相机的时间差来计算距离。ToF相机可以直接测量每个像素点的深度信息。
2. 结构光相机：结构光相机使用一种特殊的光源（例如激光器或LED投影仪）在场景上投射结构化的光图案，例如格栅或斑点。相机通过捕获投射到场景上的结构化光图案，并分析图案的形变来计算物体表面的深度信息。

测量原理

1. ToF相机：ToF相机测量时间差，因此可以在较短时间内获取深度信息，适用于实时应用。
2. 结构光相机：结构光相机需要在场景中投射光图案并捕获反射的图案，因此相对于ToF相机可能需要较长的时间来获取深度信息。

常见相机

1. ToF：Kinect V1&V2，RealSense
2. 结构光：Kinect DK

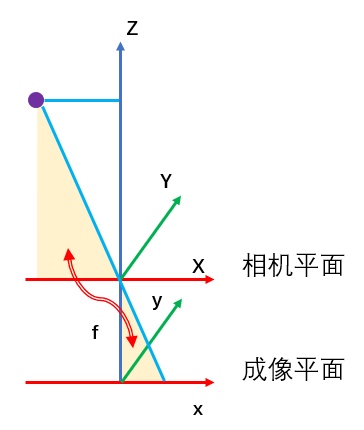
针孔相机模型

Z f = X x = Y y \frac{Z}{f}=\frac{X}{x}=\frac{Y}{y} fZ​=xX​=yY​

激光雷达投影到 2D 平面

p i m g = 1 Z K T P l i d a r p_{img} = \frac{1}{Z}KTP_{lidar} pimg​=Z1​KTPlidar​

# lidar2img: cam2img + lidar2cam
def projectPoints(pcd, img_path, lidar2img):# 1. read filesimg = cv2.imread(img_path)w, h = img.shapepoints = np.asarray(pcd.points)# 2. transform lidarvelo = np.insert(points, 3, 1, axis = 1).T# 如果x或者y小于0，那么就把整列也就是整个点，给删除了velo = np.delete(velo, np.where(velo[0, :] < 0), axis = 1)velo = np.delete(velo, np.where(velo[1, :] < 0), axis = 1)cam  = lidar2img.dot(velo)cam  = np.delete(cam, np.where(velo[2, :] < 0), axis = 1)# 3. delete invalid pixelcam[:2] /= cam[2, :]u, v, z = cam[:3]u_out = np.logical_or(u < 0, u > w)v_out = np.logical_or(v < 0, v > h)outlier = np.logical_or(u_out, v_out)cam = np.delete(cam, np.where(outlier), axis = 1)u, v, z = cam[:3]# 4. visualizefor x, y, z in zip(x, y, z):cv2.circle(img, (int(x), int(y)), 3, (0, 255, 0), -1)cv2.imshow("img", img)cv2.waitkey(0)cv2.destroyAllWindows()

多任务平衡

1. MiDaS 和 DPT 中使用帕累托优化做到多任务平衡
2. LeReS 使用课程学习做的多任务平衡，从简单到难
3. SM4Depth 使用自适应采样来做到多任务平衡

自动驾驶检测模型对 corner case 进行的针对性优化

1. 像素级异常：挡风玻璃有遮挡，隧道穿越的过曝现象，对向车辆的远光灯
   使用少样本学习，或者数据增强的方式进行训练
2. 域变换：到了环境不同的地方，到了行驶习惯不同的国家
   学习正常的数据集，同时判断一个场景是否属于OOD，即对域的匹配程度进行测量
3. 未知对象：未知的实例
   使用具有LLL，检测OOD能力的目标检测模型，比如OWOD。如果说只是在OOD能力上卓越的话，可以选择我们的Unsniffer
   对于异性物体检测，比如倒地的护栏，正在转弯的货车。可以将物体体素化，转化为占据栅格进行处理。
4. 潜在场景：行人，异常车辆
   对街道上的行人车辆进行行动预测

密集行人场景遮挡

调整目标检测的loss来处理这种场景，使检测框远离周围gt框，并靠近正确的gt框
$loss=dis(pd,gt)-dis(pd,surroundinggt)$
loss 会使得第一项越来越小，第二项越来越大

这种遮挡对跟踪的影响

1. 会导致检测算法无法准确检出人物
2. NMS的阈值难以设定，阈值过小会使得虚检增多，阈值过大则会滤掉正确框住周围目标的框

推导全连接层梯度回传

see here
全连接层的输入和输出公式如下：
$\mathbf{X}\cdot \mathbf{W}+\mathbf{B}=\mathbf{Y}$
则有Loss函数 $\mathbf{L}$ 关于 $\mathbf{X}$ 和 $\mathbf{W}$ 的导数分别为：

1. ∂ L ∂ X = ∂ L ∂ Y ⋅ W T \frac{\partial L}{\partial \mathbf{X}} = \frac{\partial L}{\partial \mathbf{Y}} \cdot \mathbf{W}^T ∂X∂L​=∂Y∂L​⋅WT
2. ∂ L ∂ W = X T ⋅ ∂ L ∂ Y \frac{\partial L}{\partial \mathbf{W}} = \mathbf{X}^T \cdot \frac{\partial L}{\partial \mathbf{Y}} ∂W∂L​=XT⋅∂Y∂L​

推导公式2的时候，把第一次两项的位置换一下

为什么多卡训练时，GPU0显存要多一些

• DataParallel会将定义的网络模型参数默认放在GPU 0上

• 这里GPU0作为master来进行梯度的汇总和模型的更新，再将计算任务下发给其他GPU，所以他的内存和使用率会比其他的高。

手写卷积

输入和输出的特征图尺寸大小关系：
n − k + 2 p s + 1 \frac{n -k+2p}{s} + 1 sn−k+2p​+1

def conv2d(inputs, kernels, bias, stride, padding):"""正向卷积操作inputs: 输入数据，形状为 (C, H, W)kernels: 卷积核，形状为 (F, C, HH, WW)，C是图片输入层数，F是图片输出层数bias: 偏置，形状为 (F,)stride: 步长padding: 填充"""# 获取输入数据和卷积核的形状C, H, W = inputs.shapeF, _, kH, kW = kernels.shape# 在输入数据的第二个轴和第三个轴上的开始和结束位置填充padding个值inputs_pad = np.pad(inputs, ((0, 0), (padding, padding), (padding, padding)))# 初始化输出数据，卷积后的图像size大小outH = (H - kH + 2 * padding) // stride + 1outW = (W - kW + 2 * padding) // stride + 1outputs = np.ones((F, outH, outW))# 进行卷积操作for i in range(outH):for j in range(outW):inputs_slice = inputs_pad[:, i * stride : i * stride + kH,j * stride : j * stride + kW]outputs[:, i, j] = np.sum(inputs_slice * kernels, axis=(1, 2, 3)) + biasreturn outputs

卷积核的参数量

一个 $F\times C\times H\times W$ 的卷积核，参数量是 $F\times C\times H\times W\times 4\mathbf{B}$

结构风险和经验风险

1. 期望风险：机器学习模型关于真实分布的平均损失称为期望风险
2. 经验风险：机器学习模型关于训练集的平均损失称为经验风险，当样本数无穷大∞的时候趋近于期望风险（大数定律）
3. 结构风险：结构风险 = 经验风险 + 正则化项

Delta K

1 T ∑ i m a x ( d / d , d / d ) \frac{1}{T}\sum_i{max(d/\mathbf{d}, \mathbf{d}/d)} T1​∑i​max(d/d,d/d)

thresh = np.maximum((gt[valid_mask]/pd[valid_mask]), (pd[valid_mask]/gt[valid_mask]))
d1 = (thresh < 1.25).mean()
d2 = (thresh < 1.25 ** 2).mean()
d3 = (thresh < 1.25 ** 3).mean()

Abs Rel

1 T ∑ i ∣ d − d ∣ d \frac{1}{T}\sum_i{\frac{|d-\mathbf{d}|}{\mathbf{d}}} T1​∑i​d∣d−d∣​

rel = np.abs(gt[valid_mask] - pd[valid_mask]) / gt[valid_mask]
rel = rel.mean()

RMSE

1 T ∑ i ( d − d ) 2 \sqrt{\frac{1}{T}\sum_i(d - \mathbf{d})^2} T1​∑i​(d−d)2 ​

rms = ((gt[valid_mask] - pd[valid_mask]) ** 2).mean()
rms = torch.sqrt(rms)

Silog

α 1 T ∑ i g 2 − λ T 2 ( ∑ i g ) 2 ， g = log ⁡ d − log ⁡ d \alpha\sqrt{\frac{1}{T}\sum_ig^2-\frac{\lambda}{T^2}(\sum_ig)^2}，g=\log d-\log \mathbf{d} αT1​∑i​g2−T2λ​(∑i​g)2 ​，g=logd−logd

valid_mask = torch.logical_and(gt > args.eval_depth_min, gt < args.eval_depth_max)
err = torch.log(gt[valid_mask]) - torch.log(pd[valid_mask])
silog_loss = 10.0 * torch.sqrt((d ** 2).mean() - 0.85 * (d.mean() ** 2))

VNL

1 V ∑ i ∣ ∣ n i − n i ∣ ∣ 1 \frac{1}{V}\sum_i{||n_i-\mathbf{n}_i||_1} V1​∑i​∣∣ni​−ni​∣∣1​

Gradient Loss

import torch
import torch.functional.nn as nndef gradient(prediction, target, mask):M = torch.sum(mask, (1, 2))diff = prediction - targetdiff = torch.mul(diff, mask)grad_x = torch.abs(diff[:, :, 1:] - diff[:, :, :-1])mask_x = torch.mul(mask[:, :, 1:], mask[:, :, :-1])grad_x = torch.mul(grad_x, mask_x)grad_y = torch.abs(diff[:, 1:, :] - diff[:, :-1, :])mask_y = torch.mul(mask[:, 1:, :], mask[:, :-1, :])grad_y = torch.mul(grad_y, mask_y)loss = torch.sum(grad_x) + torch.sum(grad_y)divisor = torch.sum(M) * 2return loss / divisor if divisor != 0 else 0class gradient_loss(nn.Module):def __init__(self, gradient_scales = 4):super().__init__()self.gradient_scales = gradient_scalesdef forward(self, prediction, target, mask):losses = []for idx in range(prediction):loss = 0pd = prediction[idx]gt = target[idx]for scale in range(self.gradient_scales):loss += gradient(pd[:, ::scale, ::scale], gt[:, ::scale, ::scale], mask[:, ::scale, ::scale])losses.append(loss)return losses.mean()

SoftMax

e q i / ∑ i ( e q i ) e^{q_i}/\sum_i(e^{q_i}) eqi​/∑i​(eqi​)

n = np.random.rand(10)
softmax_n = np.exp(n)/np.sum(np.exp(n))

SoftMax 反向传播

反向传播时对 ∂ y i ∂ x j \frac{\partial y_i}{\partial x_j} ∂xj​∂yi​​ 求导，当 $i=j$ 时，
∂ y i ∂ x j = ∂ ∂ x i ( e x i ∑ ) = y i − y i 2 \frac{\partial y_i}{\partial x_j} = \frac{\partial }{\partial x_i}(\frac{e^{x_i}}{\sum } )=y_i-y_i^2 ∂xj​∂yi​​=∂xi​∂​(∑exi​​)=yi​−yi2​
当 $i\ne j$ 时，
∂ y i ∂ x j = ∂ ∂ x j ( e x i ∑ ) = − y i ⋅ y j \frac{\partial y_i}{\partial x_j} = \frac{\partial }{\partial x_j}(\frac{e^{x_i}}{\sum } )=-y_i\cdot y_j ∂xj​∂yi​​=∂xj​∂​(∑exi​​)=−yi​⋅yj​
所以
∂ y i ∂ x j = { y i − y i ⋅ y i i = j 0 − y i ⋅ y j i ≠ j \frac{\partial y_i}{\partial x_j} =\left\{\begin{matrix} y_i-y_i\cdot y_i & i=j\\ 0\ -y_i\cdot y_j & i\ne j \end{matrix}\right. ∂xj​∂yi​​={yi​−yi​⋅yi​0 −yi​⋅yj​​i=ji=j​
即当Y为 [1, n] 的向量时：
∂ Y ∂ X = d i a g ( Y ) − Y T ⋅ Y \frac{\partial Y}{\partial X}=\mathrm{diag} (Y)-Y^T\cdot Y ∂X∂Y​=diag(Y)−YT⋅Y

CrossEntropy

− ∑ i ( p i ∗ l o g ( q i ) ) -\sum_i(p_i*log(q_i)) −∑i​(pi​∗log(qi​))

label = np.array([0, 0, 0, 0, 1])
predict = np.random.rand(5)
softmax_pd = np.exp(predict)/sum(np.exp(predict))
cel = -1*sum(label*np.log(softmax_pd))

Dropout 原理

在训练过程中，Dropout以概率p（通常取0.5）随机丢弃神经网络中的一些神经元及其连接权重。换句话说，每个神经元在每次前向传播过程中都有p的概率被“丢弃”，即将其输出设置为0。

Dropout 前向传播

对于每个训练样本，在前向传播过程中，以概率p随机选择要丢弃的神经元。被丢弃的神经元的输出设置为0，未被丢弃的神经元的输出乘以1/(1-p)的缩放因子，以保持输出值的期望不变。

Dropout 反向传播

1. 在反向传播过程中，与前向传播过程相对应，被丢弃的神经元的梯度不传播，其梯度设置为0。
2. 未被丢弃的神经元的梯度乘以1/(1-p)的缩放因子，以抵消前向传播时的缩放，从而保持梯度的期望不变。
3. 训练过程中，因为每个批次都随机丢弃了一些神经元，导致网络的结构随机变化，相当于训练了多个不同的子网络，这些子网络共享参数，但权重不同，这有助于提高模型的泛化能力。

SVM 原理

SVM是一个二分类算法，在空间里找一个超平面，将空间分为两块，其中某一类的点都在超平面上方，另一类都在超平面下方。

LR 逻辑回归

see here
二分类算法，也可以用于多分类问题。
逻辑回归分为两部分：逻辑和回归。
线性回归模型里的因变量是连续变量，而逻辑回归里的因变量可以理解为分类变量，现在我们需要用回归模型去表示这个分类，比如说大或小，黑或白。那么考虑类别之间相对的关系，我们可以用概率来表示这个问题，比如说分类为黑的概率大于白的概率时，就把样本预测为黑。所以我们可以定制一个映射关系，将负无穷到正无穷之间的数值映射成概率值，即0-1之间，就可以解决线性回归到分类问题的过渡。
最常见的激活函数是Sigmoid函数。

手写sigmoid

σ ( x ) = 1 1 + e − x \sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1​

x = 1/(1 + np.exp(-1 * x))

为什么选择 sigmoid

根据伯努利公式的指数族形式

sigmoid反向传播

σ ′ ( x ) = ( 1 1 + e − x ) ′ = σ − σ 2 \sigma^\prime (x)=(\frac{1}{1+e^{-x}} )^\prime =\sigma -\sigma^2 σ′(x)=(1+e−x1​)′=σ−σ2

Transformer

Multi-head Attention 的流程：

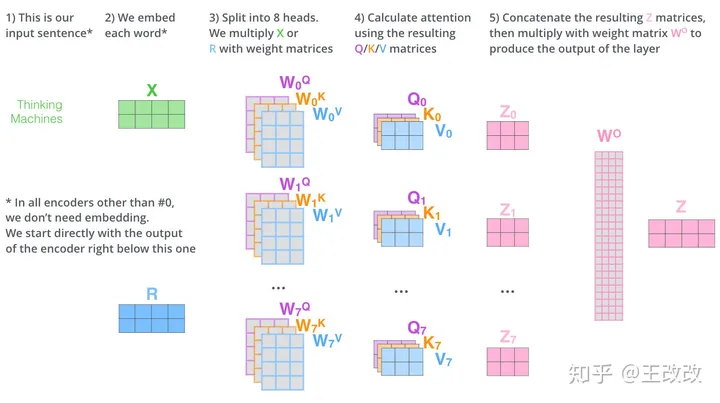
QKV是如何出来的

输入乘以三个矩阵得到输入的QKV，实现起来就是使用 nn.linear

Transformer为什么使用LN，不适用BN

1. LN适合处理变长的数据
2. 同一个通道的值是由同一个卷积核得出的，使用BN时分布更接近

Swin-Transformer

1. 对全图分 patch 进行学习
2. 对一个 patch 中的一个区域，不计算全局的相似度，而是仅计算周围一部分的像素，这个机制称为 shift window

Adam，SGD

SGD是随机梯度下降法，是最基本的优化器；
Adam是一种自适应学习率的方法，Adam是结合了SGD的一阶动量（历史梯度的累计）和RMSProp的二阶动量（历史梯度的平方累计）算法。

Adam的创新点

梯度的一阶动量，约等于近几个时刻梯度向量的平均值，这样来梯度的下降方向同时由当前的梯度方向和累计的下降方向决定，记为 $m$
梯度的二阶动量， 等于迄今为止所有梯度值的平方和，当参数更新越频繁，二阶动量就越大，学习率就会越小，记为 1 / V 1/\sqrt{V} 1/V ​
Adam 就是结合了这两项：

1. m t = β 1 ⋅ m t − 1 + ( 1 − β 1 ) ⋅ g t m_t = \beta_1 \cdot m_{t-1}+(1 - \beta_{1}) \cdot g_t mt​=β1​⋅mt−1​+(1−β1​)⋅gt​
2. V t = β 2 ⋅ V t − 1 + ( 1 − β 2 ) ⋅ g t 2 V_t = \beta_2 \cdot V_{t-1}+(1 - \beta_{2}) \cdot g^2_t Vt​=β2​⋅Vt−1​+(1−β2​)⋅gt2​

此处的 β 1 , β 2 \beta_1, \beta_2 β1​,β2​就是Adam的超参，所以梯度下降公式如下：
η t = α ⋅ m t / V t , ω t + 1 = ω t − η t \eta_t = \alpha \cdot m_t/\sqrt{V_t}, \omega_{t+1} = \omega_t-\eta_t ηt​=α⋅mt​/Vt​ ​,ωt+1​=ωt​−ηt​

如何修改SGD

1. 添加一阶动量解决震荡问题
2. 使用上一步的累计动量更新一步，用下一步的梯度方向和历史累计动量相结合，计算出当前的梯度更新方向，来解决局限于局部极小值的问题。

SGD 是否需要 shffule 数据集

需要，只有在从样本中获得顺序特征时才不 shuffle

SGD 解方程

# 定义方程，使用 SGD 算法求解 当 init=4，func=x**3+2*x-24，y=80 的解为多少
def func(x):return 3 * (x ** 2) + 2 * x - 24def loss(x, target):return (x - target) ** 2def derivative_loss(x, target, eps = 1e-8):return (loss((x + eps), target) - loss(x, target)) / epsdef solve(x, target, lr = 0.001, iters = 60000):print('init x:', x)for i in range(iters):y = func(x)if abs(y - target) < 1e-5:return xelse: grad_x = derivative_loss(y, target)x = x - grad_x * lrreturn xif __name__ == '__main__':init = 4target = 80x = solve(init, target)print(x, func(x), target)

NMS

在目标检测中，常会利用非极大值抑制算法 (NMS) 对生成的大量候选框进行后处理 (post processing) ，去除冗余的候选框，得到最具代表性的结果，以加快目标检测的效率。一般是先得到生成的所有框，然后用一个参数 score_thr 筛除置信度太低的框，再将剩余框送入 nms 函数进行抑制，nms 一般有一个 iou_thr 参数，一般为 0.5。

NMS 算法的主要流程如下所示：

根据候选框的类别分类概率做排序：A

1. 先标记最大概率矩形框 F 是我们要保留下来的；
2. 从最大概率矩形框 F 开始，分别判断 A~E 与 F 的重叠度 IOU（两框的交并比）是否大于某个设定的阈值，假设 B、D 与 F 的重叠度超过阈值，那么就扔掉 B、D；
3. 从剩下的矩形框 A、C、E 中，选择概率最大的 E，标记为要保留下来的，然后判读 E 与 A、C 的重叠度，扔掉重叠度超过设定阈值的矩形框

就这样一直重复下去，直到剩下的矩形框没有了，标记完所有要保留下来的矩形框

import numpy as npdef nms(dets, thresh):x1, y1, x2, y2 = dets[:, 0], dets[:, 1], dets[:, 2], dets[:, 3]scores = dets[:, 4]regions = (x2 - x1 + 1) * (y2 - y1 + 1)order = scores.argsort()[::-1]keep = []while order.size > 0:i = order[0]keep.append(i)xA = np.maximum(x1[i], x1[order[1:]])yA = np.maximum(y1[i], y1[order[1:]])xB = np.maximum(x2[i], x2[order[1:]])yB = np.maximum(y2[i], y2[order[1:]])inter = np.maximum(0, xB - xA + 1) * np.maximum(0, yB - yA + 1)iou = inter / (regions[order[1:]] + regions[0] - inter)idx = np.where(iou <= thresh)[0]order = order[idx + 1]return keepif __name__ == "__main__":dets = np.array([[30, 20, 230, 200, 1], [50, 50, 260, 220, 0.9],[210, 30, 420, 5, 0.8],[430, 280, 460, 360, 0.7]])thresh = 0.5keep_dets = nms(dets, thresh)print(keep_dets)print(dets[keep_dets])

SoftNMS

对NMS进行修改，对IoU高的框不直接进行删除，而是赋予一个较低的score
一般对二阶段的算法有用

IoU

def compute_iou(box1, box2):boxA = [int(x) for x in box1]boxB = [int(x) for x in box2]x1 = max(boxA[0], boxB[0])y1 = max(boxA[1], boxB[1])x2 = min(boxA[2], boxB[2])x3 = min(boxA[3], boxB[3])inter = max(0, x2 - x1 + 1) * max(0, y2 - y1 + 1)regionA = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)regionB = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)return inter / float(regionA + regionB - inter)

边缘检测算法

Sobel

图像中的边缘部分的像素值变化剧烈，属于是高频的信息，提取边缘本质上就是对图像进行求导，OpenCV 中的 Sobel 算子就近似这个过程。
因为噪声的区域的像素变化也很大，会对结果产生很大影响，所以我们首先要做的就是用高斯滤波将图像中的噪声过滤。
然后对图像进行 x 和 y 方向上的求导（运用垂直和水平的奇数大小卷积模版对图像进行卷积）。
得到图像在 x 和 y 方向上的梯度 Gx 和 Gy，然后得到总的梯度 G = G x 2 + G y 2 G = \sqrt{G_x^2+G_y^2} G=Gx2​+Gy2​ ​

Laplacian

Laplacian算子是Sobel算子的改进版，对图像求二阶导数

Pooling Layer

手写 Pooling Layer

# 手撕以max pooling为例，如果是平均pooling，只需要把np.max改成np.meandef max_pooling(inputs, pool_size, stride):"""最大池化操作inputs: 输入数据，形状为 (C, H, W)pool_size: 池化核的大小stride: 步长"""C, H, W = inputs.shape# 初始化输出数据H_out = (H - pool_size) // stride + 1W_out = (W - pool_size) // stride + 1outputs = np.zeros((C, H_out, W_out))# 进行最大池化操作for i in range(H_out):for j in range(W_out):inputs_slice = inputs[:, i * stride : i * stride + pool_size,j * stride : j * stride + pool_size]outputs[:, i, j] = np.max(inputs_slice, axis=(1, 2))return outputs

Pooling Layer 传播方式

Pooling Layer没有可以训练的参数，所以Pooling Layer只需要将误差传递到上一层，并不需要做梯度的计算，只需要保持梯度总量不变即可

1. avgpooling，直接将梯度平均分配到对应的多个像素中，可以保证梯度之和是不变的。
2. maxpooling，在正向传播时要记录最大值的index，反向传播时梯度值传递给index，其他像素的梯度为0

手写 BN

def batch_norm(inputs, gamma, beta, eps):"""批量归一化操作。N, C, H, W样本数可以看做N*H*W，CNN中，BN通常在每个通道上独立进行inputs: 输入数据，形状为 (N, C, H, W)gamma: 缩放因子，形状为 (C,)beta: 偏移因子，形状为 (C,)eps: 防止除0的小数值"""N, C, H, W = inputs.shape# 在N、H和W的维度上计算每个通道的均值和方差mean = np.mean(inputs, axis=(0, 2, 3), keepdims=True)  # (1,C,1,1)var = np.var(inputs, axis=(0, 2, 3), keepdims=True)# 计算归一化的输入。eps防止除0inputs_norm = (inputs - mean) / np.sqrt(var + eps)# 缩放和偏移outputs = gamma * inputs_norm + betareturn outputs

BN 层的作用

为了在网络的训练过程中也对数据进行归一化，方便网络的训练。
这个方法就是 BN
优点：

1. 减少了对学习率的要求
2. 破坏了原来数据的分布，一定程度上缓解了过拟合，防止每批训练中某个样本经常被挑选到
3. 减少梯度消失，加快收敛速度，提高训练精度

BN在训练和测试时的区别

1. 训练时针对每一个batch计算均值和方差
2. 测试时，使用之前训练得到的均值和方差进行归一化，并使用相同的缩放和平移参数

BN如何加速

推理时BN的参数固定，又因为卷积和BN都是线性操作，所以可以和在一起加速

过拟合

过拟合是指训练误差和测试误差之间的差距太大。模型在训练集上表现很好，但在测试集上却表现很差，也就是泛化能力差。引起的原因有 ①训练数据集样本单一，样本不足 ②训练数据中噪声干扰过大 ③模型过于复杂。防止过拟合的几种方法：

1. 增加更多的训练集或者数据增强(根本上解决问题)
2. 采用更简单点的模型(奥卡姆剃刀准则，简单的就是正确的)
3. 正则化(L1，L2)
4. 可以减少不必要的特征或使用较少的特征组合

P范数

p范数： ∣ ∣ x ∣ ∣ p = ( ∣ x 1 ∣ p + ∣ x 2 ∣ p + … + ∣ x n ∣ p ) 1 / p ||x||_p = (|x_1|^p+|x_2|^p+…+|x_n|^p)^{1/p} ∣∣x∣∣p​=(∣x1​∣p+∣x2​∣p+…+∣xn​∣p)1/p，在最后的 loss 函数中加一个正则项，将模型的权重 W 作为参数传入范数中

1范数

∣ ∣ x ∣ ∣ 1 = ( ∣ x 1 ∣ + ∣ x 2 ∣ + … + ∣ x n ∣ ) ||x||_1 = (|x_1|+|x_2|+…+|x_n|) ∣∣x∣∣1​=(∣x1​∣+∣x2​∣+…+∣xn​∣)
一范数会鼓励部分参数为0，这样只保留了对目标变量有重要影响的参数，使得部分参数为0，实现了参数的稀疏化。

2范数

∣ ∣ x ∣ ∣ 2 = ( ∣ x 1 ∣ 2 + ∣ x 2 ∣ 2 + … + ∣ x n ∣ 2 ) 1 / 2 ||x||_2 = (|x_1|^2+|x_2|^2+…+|x_n|^2)^{1/2} ∣∣x∣∣2​=(∣x1​∣2+∣x2​∣2+…+∣xn​∣2)1/2
二范数对参数的平方和进行监督，会鼓励参数整体偏向较小值，防止模型参数过大（参数过大时会对数据中的噪声和随机波动过度拟合，并不是学习到了一般化的规律），避免过拟合发生。

欠拟合

欠拟合是指模型不能在训练集上获得足够低的误差。换句换说，就是模型复杂度低，模型在训练集上就表现很差，没法学习到数据背后的规律。防止欠拟合的几种方法：

1. 采用更大的模型
2. 采用更强的特征

训练出现NaN

有可能是除以 0 或者是出现了 log(0) 的情况

目标检测

两阶段检测模型

使用相应的Region Proposal算法从输入图片中生成建议目标候选区域，将所有的候选区域送入分类器进行分类。

R-CNN

contribution:
1.使用CNN进行基于区域的定位和物体分割
2.监督训练样本数紧缺时，在额外的输入上需训练的模型经过fine-tuning可以获得很好的效果。

Pipeline：
1.基于图片提出若干Region Proposal，文中使用的是Selective Serach算法。该算法将图片划分为多个patch，每个patch之间计算颜色相似性，纹理相似性，相近的patch进行合并。
2.训练N个SVM分类器来判断框是否属于这个类别，SVM是二分类的，输出True表示属于这个类别，输出False表示不属于这个类别
3.使用NMS去除相交的多余的框。NMS中会对每个类别的框分别进行类内的NMS，在这一类中，首先挑选置信度最大的框，然后把这个框和与这个框IoU过大的框都从候选框中删除，重复上一过程直到没有候选框。最后把置信度小于一定阈值的框删除，得到最后的结果。
4.最后预测框的偏移量，对这些框进行回归修正。

Fast R-CNN

将基础网络在图片整体上运行（共享了大部分计算）后，再传入R-CNN子网络。

Faster R-CNN

提出了RPN网络使得目标检测任务端到端地完成。RPN中使用多个anchor提出目标框。

优点

缺点

Unsniffer

1.使用GOC得分抑制包围过大的框，部分包围的框，提升全包围的框
2.使用ncut对簇内进行NMS挑选框
3.使用负能量抑制对非物体的框进行抑制

单阶段检测模型

YOLO

网络首先输出 SSchannel 的特征图，其中SS表示输出SS个网格。在此之后每个网格会预测B个框，每个框带有4个坐标值和1个置信度得分，再加上大小为C的类别信息，网络最后的输出为SS(5*B+C)

更快，但是性能不如2-stage的方法。使用全图的信息，把背景错认为物体的情况较少。泛化能力强

SSD (Single Shot multibox Detector)

YOLO是对每个patch进行检测，容易造成漏检测，并且对物体的尺度比较敏感。

改进：
1.使用多尺度的feature map，将vggnet多个尺度的特征值输入回归器中提升了对小物体的检测效率。
2.采用了更多的achor box，并且基于box对物体的类别进行了预测。

优点

缺点

选择原因：
1.计算平台：
树莓派缺少GPU，因此首选tflite，而非GPU下的tensorRT，手机端的ncnn。tflite官方推荐的有ssd，yolov5，efficientnetv3，efficientnetv2
2.检测性能：
相同图片下，efficientnetv2无法检测到苹果，yolov5给出的框和置信度不高，ssd和efficientnetv3给出的框较好，且置信度较高。
距离较远的情况下，ssd（输入尺寸小）和efficientnetv3检测能力下降，yolo能勉强框住物体。
3.运行速度：
模型大小ssd，efficientnetv3，yolo为：1:2:3
FPS为：11：7：1

运动控制

PID

比例积分微分控制，p代表相应时间，i代表累计误差，d代表稳定性

KCF

将图像通过滤波器处理，把图像和滤波器的输出通过傅里叶变换，计算相应图，将相应图逆傅里叶变换到空域得到最大响应值的位置，作为目标估计的当前位置

单目深度估计

SM4Depth

SimMIM 预训练

SimMIM随机mask掉输入图像的一部分patch，
然后通过encoder-decoder来预测masked patchs的原始像素值

PST

class pst(nn.Moudle):def __init__(self, embedding_dims = 128, num_heads = 4, num_layers=4):super.__init__()encoder_layers = nn.TransformerEncoderLayer(embedding_dims, num_heads, dim_feedforward=1024)self.TransformerEncoder = nn.TranformerEncoder(encoder_layers, num_layers=num_layers)self.PositionEncoding = nn.Parameter(torch.rand(500, embedding_dim), requires_grad=True)def foward(self, x):embeddings = x.flatten(2)  # B, E, Sembeddings = nn.functional.pad(embeddings, (1, 0, 0, 0, 0, 0))  # B, E, S + 1embeddings = embeddings + self.PositionEncoding[:embeddings.shape(2), :].T.unsqueeze(0)embeddings = embeddings.permute(2, 0, 1)  # S + 1, B, Ex = self.TransformerEncoder(embeddings)return x

Bin-based Depth Estimation

# bins = [256]
bins = (args.train_depth_max - args.train_depth_min) * (bins / torch.sum(bins) + 0.001)
bins = nn.functional.pad(bins, (1, 0), mode = 'constant', value = 0.001)
bins = torch.cumsum(bins)
centers = (bins[:-1] + bins[1:]) * 0.5
centers = centers.view(256, 1, 1)

训练集

ScanNet，DIODE，Hypersim，ApolloScape，UASOL

轻量级单目深度估计

CVPR 2022 WorkShop

1. TCL

• 类似于UNet的结构，将输入图片下采样到原图的1/4，然后传递给MobileNetV3
• 删除了MobileNetV3的最后一层，来提升网络的速度
• Encoder的输出被送到CLB中，最后x10缩放到原始的大小
• 使用silog作为损失函数

2. HIT

• 多种Loss：silog，gradient，vnl
• 知识蒸馏
• 数据增强
• 设计合适的特征融合模块
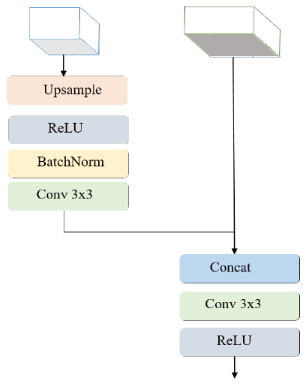  或者

DANet

1. EfficientNetb0
2. 可分离卷积
3. 降低深度分类个数
4. 深度图直接x2作为最后输出

双目深度估计

视差转深度的公式推导

D e p t h = B a s e l i n e × F o c a l L e n g t h D i s p a r i t y × 1000 Depth = \frac{Baseline \times Focal Length}{Disparity\times 1000} Depth=Disparity×1000Baseline×FocalLength​

轻量级平台配置

TFLite 配置流程

1. 安装 TFLite 虚拟环境
2. 安装 TFLite 解释器和下载 TFLite 模型

TensorRT

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！