求解最大连续子序列和问题（Java）蛮力法+分治法

求解最大连续子序列和问题

【问题描述】
给定一个有n（n>=1）个整数的序列，要求求出其中最大连续子序列的和。
【样例输入】
6
-2 11 -4 13 -5 -2
【样例输出】
20

【问题求解】
对于含有N个整数的序列a[0…n-1]，若n=1，表示该序列仅含一个元素，如果该元素大于0，则返回该元素；否则返回0。

● 暴力枚举法①：用两层循环枚举起点和终点，尝试所有的子序列，然后计算每个子序列的和，然后找到其中最大的即可。

public static int maxSubSum(int[] a) {int maxSum = 0;for (int i = 0; i < a.length; i++) {int tempSum = 0;for (int j = i; j < a.length; j++) {tempSum += a[j];		        if (tempSum > maxSum) {	 //判断最大值       	  maxSum = tempSum;}}}return maxSum;}

★时间复杂度：O(n∧2),对于较大的序列来说，是无法承受的
暴力枚举法②：当序列和<0时，则直接跳过执行即可

public static int maxSubSum(int a[]){int maxSum=0,thisSum=0;for ( int j=0;j<a.length;j++){thisSum += a[j];if (thisSum>maxSum) {maxSum=thisSum;} else if (thisSum<0) {thisSum=0;}}return maxSum;}

★时间复杂度：O(n),这个改进方法是时间复杂度最小的方法，推荐使用
● 分治法：若n>1,采用分治法求解最大连续子序列时，取其中位置mid=[(n-1)/2],该子序列只可能出现3个地方。
①该子序列完全落在左半部即a[0…mid]中。采用递归求出其最大连续子序列和maxLeftSum。

②该子序列完全落在右半部即a[mid+1…n-1]中。采用递归求出其最大连续子序列和maxRightSum.

③该子序列跨越序列a的中部而占据左右两部分，即，最大和的连续子序列中含有a[mid].

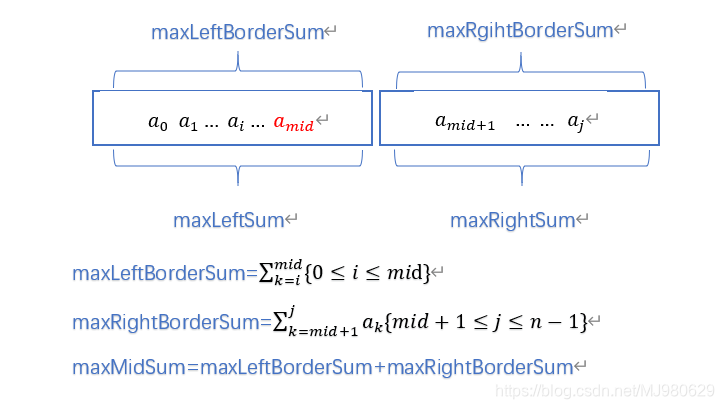
○ 最终，整个序列a的最大连续子序列和为maxLeftSum,maxRightSum,maxMidSum中的最大值。

结果：max3
(maxLeftSum,maxRightSum,maxMidSum)

例：a[5]={-2,11,-4,13,-5,-2]
解:n=6,mid=(0+5)/2=2.划分a为a[0…2]和a[3…5]，递归求出左部分最大连续子序列和为11，右部分为13，再求出以a[mid]=-4为中心的最大连续子序列和为20（11，-4，13），最终max{11，13，20}=20

private static int maxsubSum(int[] a, int left, int right) {
//求a[left..high]序列中最大连续子序列和int i,j;long maxLeftSum,maxRightSum;long maxLeftBorderSum,leftBorderSum;long maxRightBorderSum,rightBorderSum;if (left == right)     //子序列只有一个元素时if (a[left] > 0)   //该元素大于0时返回它return a[left];else               //该元素小于或等于0时返回0return 0;int mid = (left + right) / 2;   maxLeftSum = maxsubSum(a, left, mid);maxRightSum =maxsubSum(a, mid+1, right);maxLeftBorderSum = 0, leftBorderSum = 0;for (int i = mid; i >= left; i--) {      //求出以左边加上a[mid]元素leftBorderSum += a[i];               //构成的序列的最大和if (leftBorderSum > maxLeftBorderSum)maxLeftBorderSum = leftBorderSum;}maxRightBorderSum = 0, rightBorderSum = 0;for (int j = mid + 1; j <= right; j++) {  //求出a[mid]右边元素          rightBorderSum += a[j];           //构成的序列的最大和if (rightBorderSum > maxRightBorderSum)maxRightBorderSum = rightBorderSum;}return Math.max(Math.max(maxLeftSum, maxRightSum), maxLeftBorderSum + maxRightBorderSum);     

【算法分析】
设求解序列a[0…n-1]最大连续子序列和的执行时间为T(n),第(1),(2)两种情况的执行时间为T（n/2），第(3)种情况的执行时间为O（n）,所以得到以下递推式：

 T(n)=1                     当n=1T(n)=2T(n/2)+n             当n>1

★时间复杂度：

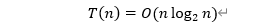
源代码

import java.util.Scanner;
import java.util.*;
public class Main{public static void main(String[] args) {Scanner sc=new Scanner(System.in);int n=sc.nextInt();int arr[]=new int[n];for(int i=0;i<n;i++) {arr[i]=sc.nextInt();}System.out.println(maxSubSum1(arr));System.out.println(maxSubSum2(arr));}public static int maxSubSum1(int[] a) {int maxSum = 0;for (int i = 0; i < a.length; i++) { int tempSum = 0;for (int j = i; j < a.length; j++) {tempSum += a[j];		        if (tempSum > maxSum) {	        	  maxSum = tempSum;}}}return maxSum;}public static int maxSubSum2(int[] a) {return subSum(a, 0, a.length - 1);}public static int subSum(int[] a, int left, int right) {//求a[left..high]序列中最大连续子序列和	        long maxLeftSum,maxRightSum;long maxLeftBorderSum,leftBorderSum;long maxRightBorderSum,rightBorderSum;if (left == right)     //子序列只有一个元素时if (a[left] > 0)   //该元素大于0时返回它return a[left];else               //该元素小于或等于0时返回0return 0;int mid = (left + right) / 2;   maxLeftSum = subSum(a, left, mid);maxRightSum =subSum(a, mid+1, right);maxLeftBorderSum = 0;leftBorderSum = 0;for (int i= mid; i >= left; i--) {      //求出以左边加上a[mid]元素leftBorderSum += a[i];               //构成的序列的最大和if (leftBorderSum > maxLeftBorderSum)maxLeftBorderSum = leftBorderSum;}maxRightBorderSum = 0; rightBorderSum = 0;for (int j = mid + 1; j <= right; j++) {  //求出a[mid]右边元素          rightBorderSum += a[j];           //构成的序列的最大和if (rightBorderSum > maxRightBorderSum)maxRightBorderSum = rightBorderSum;}return (int) Math.max(Math.max(maxLeftSum, maxRightSum), maxLeftBorderSum + maxRightBorderSum);} 
}

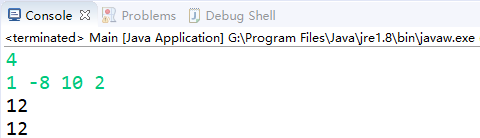
【测试结果】

若非李白会编程，序列之和均分支；遥看递归云间纵，生死看淡程序员。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！