最长公共子序列nlogn求法

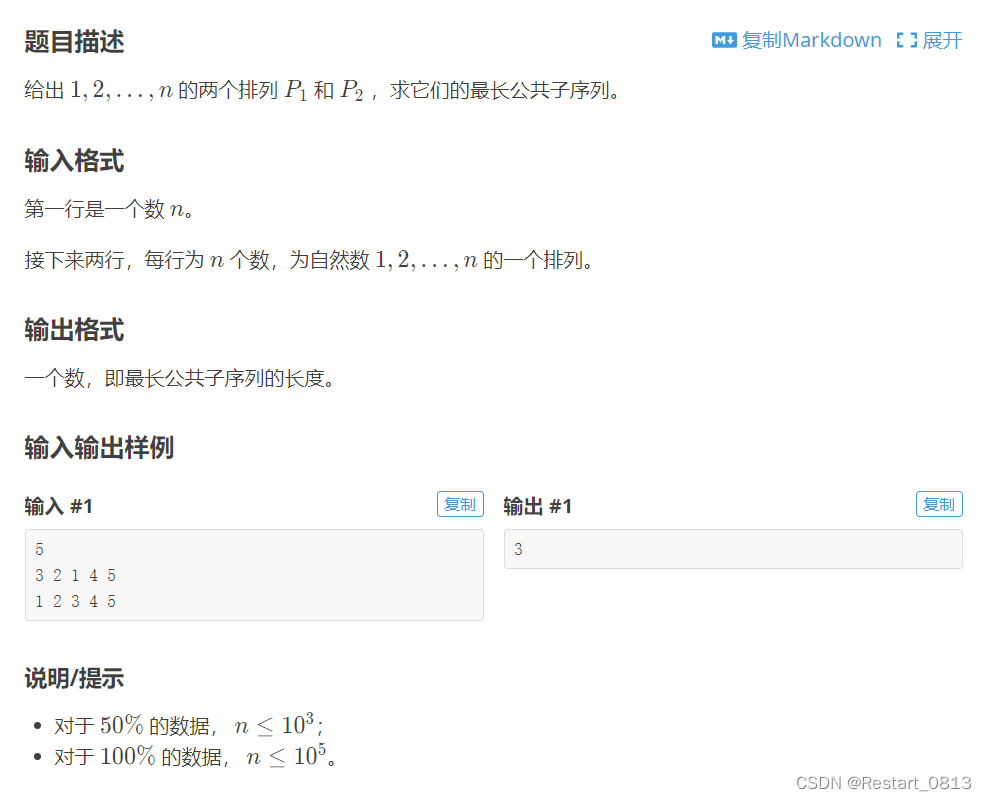
首先我们可以看到，普通的 O ( n 2 ) O(n^2) O(n2)的求法是不现实的，因为最大的数据量是$1e5$

我们考虑这么一个变化，以样例为例子
$3-2-1-4-5$
我们将其映射为
$p1:1-2-3-4-5$
并且用一个数组来记录这个映射

那么对于第二组数据
$1-2-3-4-5$,我们可以将其映射为
$p2:3-2-1-4-5$

显然的，我们只需要求出p1和p2的lcs就可以了，我们发现p1是一个递增序列，因此我们只用在p2中求出最长递增序列的就可以了。

#include 
using namespace std;
#define int long long
const int N=2e5+50;
int change[N];
int a[N];
int b[N];
int n;
int f[N];
int cnt;
signed main()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i];change[a[i]]=i;}for(int i=1;i<=n;i++){cin>>b[i];b[i]=change[b[i]];}f[++cnt]=b[1];for(int i=2;i<=n;i++){if (b[i]>f[cnt]){f[++cnt]=b[i];}else//<={int pos=lower_bound(f+1,f+1+cnt,b[i])-f;f[pos]=b[i];}}cout<<cnt;return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！