欢迎订阅《FPGA学习入门100例教程》、《MATLAB学习入门100例教程》

目录

一、理论基础

二、核心程序

三、测试结果

一、理论基础

算法分为2个部分：

第一部分是鱼提取：

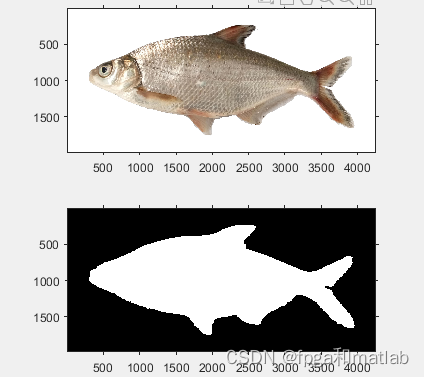
        首先更加像素判断，将鱼的背景因素去除，这个主要是像素判断，包括背景中的白色背景以及蓝色字体背景。

       这些背景去除之后，将得到一个鱼的大致轮廓。

       然后将提取的鱼进行颜色分解，即RGB转换为HSV，然后使用S通道，进行二值化处理，即，即im2bw这个函数，二值化处理之后，去掉图像中的小的噪声，即bwareaopen这个函数，

然后进行填充处理，即将鱼区域中的小的空洞区域进行填充，

      最后，通过腐蚀操作，将鱼边缘部分一些不平稳的消除。实现鱼的抠图操作。

     对鱼边缘提取和记录计算：

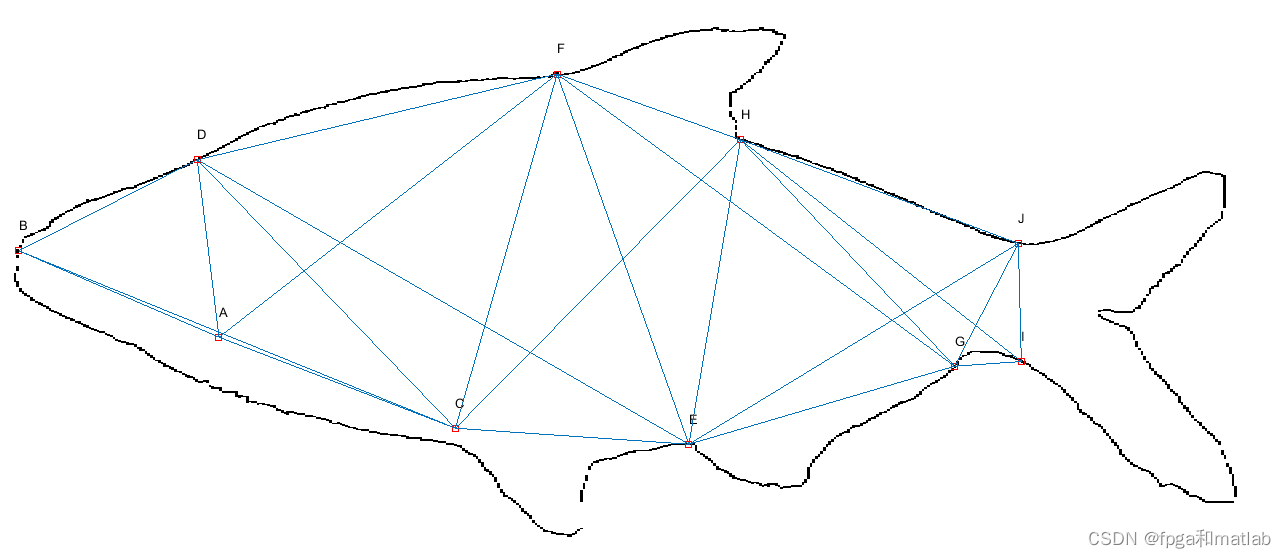
     通过edge这个函数，进行sobel边缘提取。可以提取鱼的边缘轮廓。

有了轮廓之后，进行边缘坐标点的定位。

这里，首先确定鱼嘴巴上的点，然后根据鱼身体的各个部分比例，依次提取各个点的位置。

二、核心程序

clc;
clear;
close all;
warning off;
addpath 'func\'%读取图片
I0      = imread('images\test.jpg');I1      = 1-im2bw(rgb2gray(I0),0.9999);
%去除小的连通域
I2      = bwareaopen(I1,100000);
%腐蚀
se1     = strel('disk',5);
I3      = imerode(I2,se1);
%填充
I3      = imfill(I3,'holes');figure;
subplot(211);imshow(I0);
subplot(212);imshow(I3);
%边缘提取
I4 = edge(I3,'sobel');%端点提取和连线
%第80个点基本就是B点
[R,C] = size(I4);
[Y,X] = find(I4==1);
Xb    = X(80);
Yb    = Y(80);
%D
for i = 1:length(X)if sqrt((Xb - X(i))^2 + (Yb - Y(i))^2) >= 600 & sqrt((Xb - X(i))^2 + (Yb - Y(i))^2) <= 601 & i<3000Xd = X(i);Yd = Y(i);end
end
%A
for i = 1:length(X)if sqrt((Xb - X(i))^2 + (Yb - Y(i))^2) >= 700 & sqrt((Xb - X(i))^2 + (Yb - Y(i))^2) <= 710 & i<3000 & Y(i)>1.2*YdXa = X(i)+20;Ya = Y(i)-150;end
end
%F
for i = 1:length(X)if sqrt((Xd - X(i))^2 + (Yd - Y(i))^2) >= 1100 & sqrt((Xd - X(i))^2 + (Yd - Y(i))^2) <= 1110 & i > 1000Xf = X(i);Yf = Y(i);end
end
%H
for i = 1:length(X)if sqrt((Xf - X(i))^2 + (Yf - Y(i))^2) >= 580 & sqrt((Xf - X(i))^2 + (Yf - Y(i))^2) <= 585 & Y(i)>1.05*Yf & i > 2000Xh = X(i);Yh = Y(i);end
end
%J
for i = 1:length(X)if sqrt((Xh - X(i))^2 + (Yh - Y(i))^2) >= 880 & sqrt((Xh - X(i))^2 + (Yh - Y(i))^2) <= 890 & i > 2000Xj = X(i);Yj = Y(i);end
end
%I
for i = 1:length(X)if sqrt((Xj - X(i))^2 + (Yj - Y(i))^2) >= 325 & sqrt((Xj - X(i))^2 + (Yj - Y(i))^2) <= 355 & Y(i)>1.2*Yj & X(i) < 1.05*Xj &  X(i) > 0.95*XjXi = X(i);Yi = Y(i);end
end%G
for i = 1:length(X)if sqrt((Xi - X(i))^2 + (Yi - Y(i))^2) >= 200 & sqrt((Xi - X(i))^2 + (Yi - Y(i))^2) <= 210 & X(i) < Xj & Y(i)>YiXg = X(i);Yg = Y(i);end
end%E
for i = 1:length(X)if sqrt((Xg - X(i))^2 + (Yg - Y(i))^2) >=830 & sqrt((Xg - X(i))^2 + (Yg - Y(i))^2) <= 840 & X(i) < Xg & Y(i)>YiXe = X(i);Ye = Y(i);end
end%C
for i = 1:length(X)if sqrt((Xe - X(i))^2 + (Ye - Y(i))^2) >=700 & sqrt((Xe - X(i))^2 + (Ye - Y(i))^2) <= 710 & X(i) < XeXc = X(i);Yc = Y(i)-50;end
end

三、测试结果

A16-62

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！