数据结构与算法 | 二叉树的实现

前几章实现了二叉树的顺序结构和二叉树的几种遍历，这次就来实现二叉树的链式结构

数据结构

typedef char BTDataType;
typedef struct BTNode
{BTDataType data;struct BTNode* left;struct BTNode* right;
}BTNode;

实现的接口

// 通过前序遍历的数组构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
//二叉树高度
int BinaryTreeHigh(BTNode* root);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

因为链式二叉树主要使用递归来创建的，所以这里所有的实现用递归就会更容易理解

二叉树的创建

BTNode* BinaryTreeCreate(BTDataType* arr, int n, int* pi)
{if ('#' == arr[*pi]){++(*pi);return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->data = arr[(*pi)++];root->left = BinaryTreeCreate(arr, n, pi);root->right = BinaryTreeCreate(arr, n, pi);return root;
}

**每当我们读取到#就说明当前节点是空节点，跳过该节点后返回空。
如果不是空节点，则将数据放入根节点，并递归下去创建左子树和右子树。
**

二叉树的销毁

// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{BTNode* node = root;if (!node)return;BinaryTreeDestory(node->left);BinaryTreeDestory(node->right);free(node);node = NULL;
}

从根节点出发，如果根节点不为空则递归下去销毁左右子树，如果某一节点为空则返回。

二叉树的结点数

int BinaryTreeSize(BTNode* root)
{if (!root)return 0;return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

如果当前节点为空则返回0，不为空则递归进入左右子树，如果存在节点则+ 1，最后到根节点时返回的是节点数

二叉树的叶子节点数

int BinaryTreeLeafSize(BTNode* root)
{if (!root)return 0;if (!root->right && !root->left)return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

这个和上面思路类似，因为叶子节点不存在左右子树，所以只当左右子树为空的时候才返回1。

返回第K层的节点数

int BinaryTreeLevelKSize(BTNode* root, int k)
{if (!root)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

还是和前面类似，这里返回的是第k层，每进入一层则k - 1，直到K = 1时说明已经进入了第k层， 这时再返回1

二叉树的高度

int BinaryTreeHigh(BTNode* root)
{if (!root)return 0;int leftHigh = BinaryTreeHigh(root->left);int rightHigh = BinaryTreeHigh(root->right);return leftHigh < rightHigh ? rightHigh + 1 : leftHigh + 1;
}

这一段光看代码可能比前面的稍微难理解一点，其实就是递归访问左右子树，对比那边高，因为递归的函数调用类似与栈，后进先出，所以最开始返回的是最深处也就是叶子节点的值和空节点，例如最底层的叶子节点的左右子树都为空，则返回左子树高0 + 1（因为对比条件是leftHigh < rightHigh ，等于时则左+1），然后一层一层往上，当某节点的一个子树大于另一个子树时，说明大的子树比小的高，返回高子树的层数 + 本节点的这一层1，这样递归回到根节点时，返回的就是二叉树的高度

查找二叉树节点

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{BTNode* node;if (!root)return NULL;if (root->data == x)return root;node = BinaryTreeFind(root->left, x);if (node)return node;node = BinaryTreeFind(root->right, x);if (node)return node;return NULL;}

当节点为查找值时返回节点，其他都返回空，但是这里又有一个小问题，就是因为递归的后进先出，所以我们直接返回的情况下只有在根节点的左右子树的情况下根节点才能直接接收到返回节点，所以我们需要想办法将返回节点保存下来。
因为只有节点为查找值时返回节点，其他都返回空，所以我们可以接收每次递归进入左右子树后的返回值并判断，如果返回值不为空，则直接返回这个返回值，因为不为空的情况下只可能是目标节点。

前序遍历、中序遍历、后序遍历、层序遍历

// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (!root)return;printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (!root)return;BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);}// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (!root)return;BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%c ", root->data);
}// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if(root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* node = QueueFront(&q);QueuePop(&q);printf("%c ", node->data);if(node->left)QueuePush(&q, node->left);if(node->right)QueuePush(&q, node->right);}printf("\n");QueueDestroy(&q);
}

四种遍历方式上一节讲过了，这里就直接给出代码。

判断二叉树是否是完全二叉树

在第一节介绍过，完全二叉树是所有节点都是连续的，不存在有右子树而没有左子树的情况，所以我们可以利用这个特性，结合层序遍历来完成判断，只要层序遍历时遍历到空节点停止后，如果后面的节点还存在值，则说明不是完全二叉树

同样，这里需要用到队列，队列的实现在前面有讲过
https://blog.csdn.net/qq_35423154/article/details/104360090

int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (1){BTNode* node = QueueFront(&q);if (!node)break;elseQueuePop(&q);QueuePush(&q, node->left);QueuePush(&q, node->right);}while (!QueueEmpty(&q)){BTNode* node = QueueFront(&q);if (node){QueueDestroy(&q);return 0;}elseQueuePop(&q);}QueueDestroy(&q);return 1;
}

思路如下，首先将根节点入队列，然后如果根节点不为空，则出节点，将左右子树（包括空节点）入队列，不停循环，直到队首为空节点时跳出循环，也就是遇到了第一个空。这时候就存在两种情况，后面全为空，为完全二叉树，或者存在一个不为空，不是完全二叉树。

接下来开始检查队列剩下元素，如果当前节点为空则pop出队，不为空则说明这个节点不是空节点，说明不是完全二叉树，返回0。如果全部为空则说明是完全二叉树，返回1。

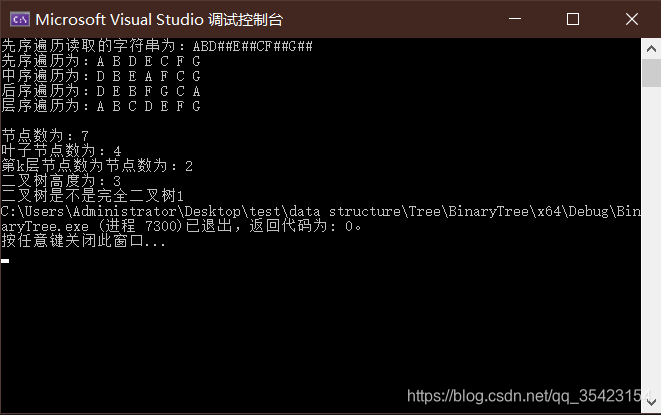
完整代码
头文件

#include
#includetypedef char BTDataType;
typedef struct BTNode
{BTDataType data;struct BTNode* left;struct BTNode* right;
}BTNode;#include "LinkedQueue.h"// 通过前序遍历的数组构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
//二叉树高度
int BinaryTreeHigh(BTNode* root);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

函数实现：

#include "BinaryTree.h"
#include "LinkedQueue.h"//创建二叉树
BTNode* BinaryTreeCreate(BTDataType* arr, int n, int* pi)
{if ('#' == arr[*pi]){++(*pi);return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->data = arr[(*pi)++];root->left = BinaryTreeCreate(arr, n, pi);root->right = BinaryTreeCreate(arr, n, pi);return root;
}
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{BTNode* node = root;if (!node)return;BinaryTreeDestory(node->left);BinaryTreeDestory(node->right);free(node);node = NULL;
}
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (!root)return 0;return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (!root)return 0;if (!root->right && !root->left)return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
// 二叉树第k层节点个数int BinaryTreeHigh(BTNode* root)
{if (!root)return 0;int leftHigh = BinaryTreeHigh(root->left);int rightHigh = BinaryTreeHigh(root->right);return leftHigh < rightHigh ? rightHigh + 1 : leftHigh + 1;
}int BinaryTreeLevelKSize(BTNode* root, int k)
{if (!root)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{BTNode* node;if (!root)return NULL;if (root->data = x)return root;node = BinaryTreeFind(root->left, x);if (node)return node;node = BinaryTreeFind(root->right, x);if (node)return node;return NULL;}// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (!root)return;printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (!root)return;BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);}// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (!root)return;BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%c ", root->data);
}// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if(root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* node = QueueFront(&q);QueuePop(&q);printf("%c ", node->data);if(node->left)QueuePush(&q, node->left);if(node->right)QueuePush(&q, node->right);}printf("\n");QueueDestroy(&q);
}int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (1){BTNode* node = QueueFront(&q);if (!node)break;elseQueuePop(&q);QueuePush(&q, node->left);QueuePush(&q, node->right);}while (!QueueEmpty(&q)){BTNode* node = QueueFront(&q);if (node){QueueDestroy(&q);return 0;}elseQueuePop(&q);}QueueDestroy(&q);return 1;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！