文章目录

• 并查集的原理
• 并查集的实现
• 例题

并查集的原理

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个
单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一
个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find
set)。

并查集底层通常常用数组存储，并且存在以下特性：

1. 数组的下标对应集合中元素的编号
2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数
3. 数组中如果为非负数，代表该元素双亲在数组中的下标

这里举一个例子，假设今年秋季大一开学时班级共有10名学生，上海3人，海南4人，广东3人。这些学生都是刚进入校园，彼此都不认识，一开始每一个学生都是一个独立的小团体，现在用下标来为学生们编号，顺序按照上面的所在地。

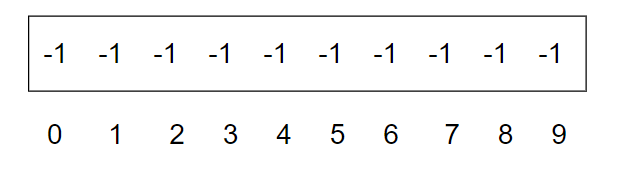
因为来自同一个地方的学生他们从小的风俗习惯都十分接近，并且也有共同话题，所以很快他们就形成了自己的小团体

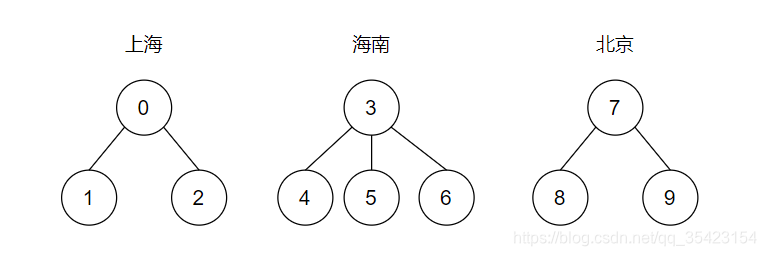
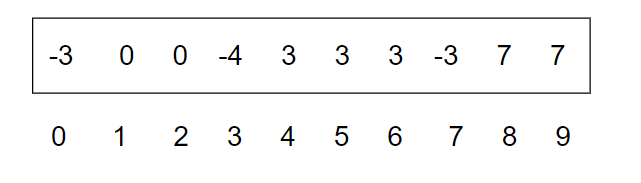
紧接着，因为来自上海的2号同学和来自海南的5号同学是同一个宿舍的，所以他也很快融入了2号的朋友圈，并且把自己的朋友也介绍给2号，所以此时上海和海南的朋友圈集合开始交集


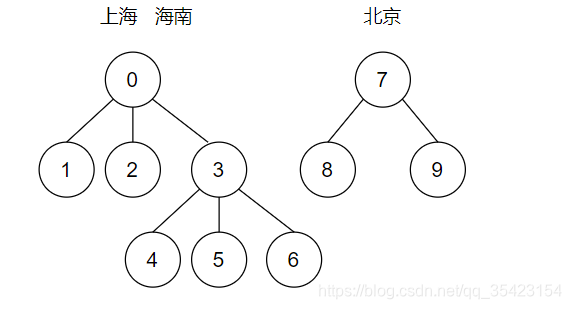
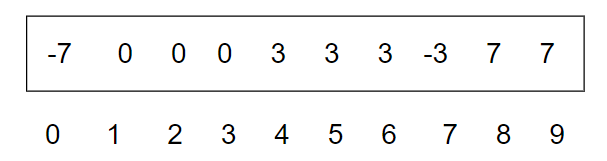
通过这个结构，可以确认此时存在着两个集合，集合上海-海南共有7人，集合背景共有3人。

通过这种并查集的结构，可以用来解决以下问题

1. 查找元素属于哪个集合
2. 查看两个元素是否属于同一个集合
3. 将两个集合归并成一个集合
4. 集合的个数

并查集的实现

class UnionFindSet
{
public://初始化时将所有元素置为-1，表示每一个都是独立的集合UnionFindSet(size_t size): _ufs(size, -1),_rank(size, 1){}//找到某一个集合的根int FindRoot(int index){//根节点的值为负数，如果不为负则说明不是根节点，继续找while (_ufs[index] >= 0){//因为每个节点存储自己父节点的下标，所以往上继续查找index = _ufs[index];}return index;}//将两个集合并集bool Union(int x1, int x2){int root1 = FindRoot(x1);int root2 = FindRoot(x2);//本来就是一个集合，不需要合并if (root1 == root2){return false;}/*优化，让小集合挂在大集合上，减少查询次数if (_rank[root1] < _rank[root2 ]) {swap(root1 , root2);}_rank[root1] += _rank[root2];*///选择root1作为根，将root2所在集合合并到root1中_ufs[root1] += _ufs[root2];//将另一个的父节点设置为root1_ufs[root2] = root1;return true;}//求集合的个数，即负节点的个数size_t count() const{size_t count = 0;for (auto it : _ufs){if (it < 0){count++;}}return count;}private:std::vector<int> _ufs;std::vector<int> _rank; //用于加速查找
};

例题

并查集一般可以解决以下问题：

1. 查找元素属于哪个集合
2. 查看两个元素是否属于同一个集合
3. 将两个集合归并成一个集合
4. 集合的个数

例如leetcode-547.朋友圈就属于上面的第四种问题，也就是我最开始举例的那个问题

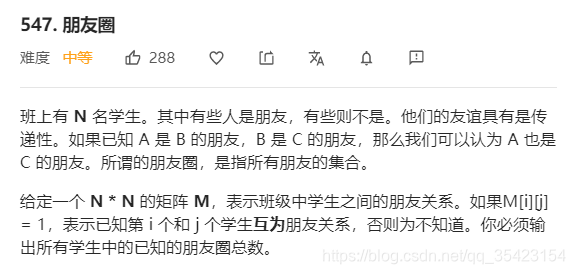
class Solution {
public:int findCircleNum(vector<vector<int>>& M) {UnionFindSet ufs(M.size());/*M[i][j] = x 代表着i同学和j同学之间的关系为x*/for(int i = 0; i < M.size(); i++){for(int j = 0; j < M[i].size(); j++){//如果为朋友，则将两人并集if(M[i][j] == 1){ufs.Union(i, j);}}}return ufs.count();}
};

leetcode-990. 等式方程的可满足性就属于上面的第二类问题

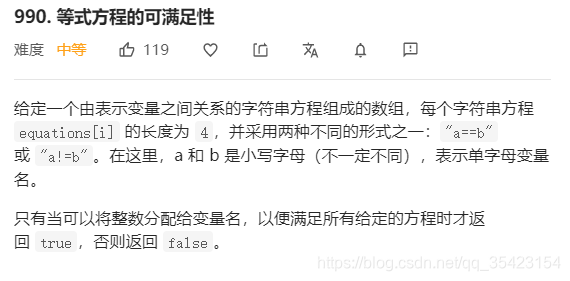
主要思路就是判断不等集合是否与相等集合产生交集

/*思路:两次遍历数据，第一次将所有相等集合并集。第二次查找相等集合中是否有数据存在于不等集合，如果有则说明产生互斥，返回false
*/
class Solution {
public:bool equationsPossible(vector<string>& equations) {UnionFindSet ufs(26);for(const auto& str : equations){//将相等的数据放入集合中if(str[1] == '='){ufs.Union(str[0] - 'a', str[3] - 'a');}}for(const auto& str : equations){//判断不等的两端是否处于集合，如果有则说明产生互斥，不满足条件，返回falseif(str[1] == '!'){if(ufs.FindRoot(str[0] - 'a') == ufs.FindRoot(str[3] - 'a')){return false;}}}return true;}
};

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！