文章目录

• KMP
• 原理
• next数组的构建
• 代码实现

KMP

一提到字符串匹配算法，想必大家脑海中想到的第一个必然就是KMP算法，KMP算法的全称叫做KnuthMorrisPratt算法，与上一篇博客中介绍的BM算法一样，它的核心也是通过滑动来减少不必要的匹配。

原理

与BM算法不同，KMP算法是从前往后进行比较的，并且其将专注点放在已匹配的前缀上，为了方便理解，在这里我们还是使用BM算法中的好前缀和坏字符的概念。

例如下列字符串

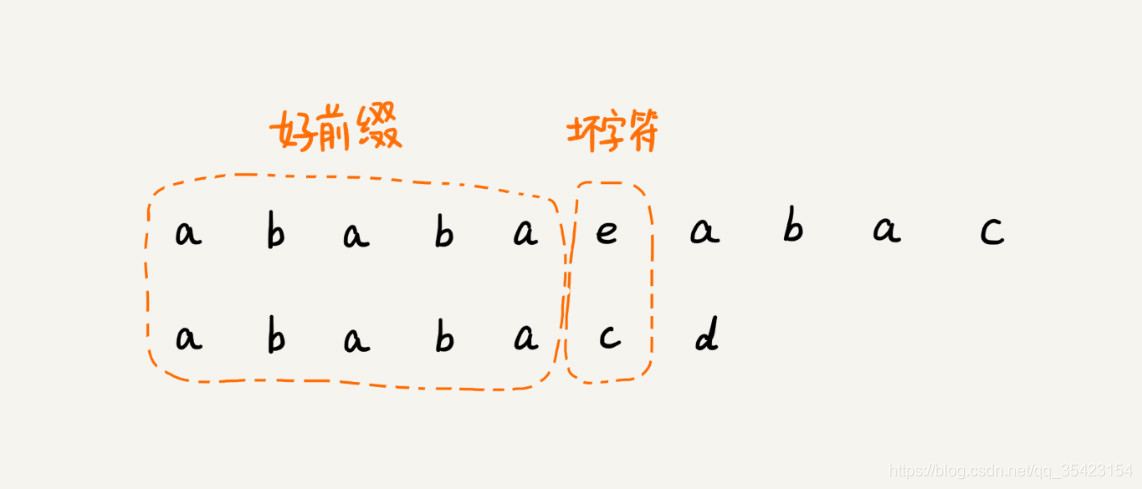
还是老样子，我们试图在已匹配的前缀中找到某种规律，使得我们能够一下进行大量的滑动，我们此时就对好前缀进行分析。

此时我们发现，对于好前缀来说，其存在两组完全相同的前缀和后缀，分别是aba和a。

此时我们就可以利用这个相同的后缀，直接将模式串对其到后缀的起始位置，为了保证偏移量最大，我们选择其中最长的那一组，如下图

为了表述方便，我将这组前后缀子串分别称为最长可匹配前缀子串和最长可匹配前缀子串

KMP的整体思路就是在已匹配的前缀当中寻找到最长可匹配后缀子串和最长可匹配前缀子串，在下一轮直接把两者对齐，从而实现模式串的快速滑动

next数组的构建

为了避免每次都要去寻找这组最长匹配的前后缀，我们将其缓存到一个数组中，等到使用的时候再去取，这个数组也就是我们经常提到的next数组，而它的构建也是KMP算法中最难理解的地方

数组的下标是每个前缀结尾字符下标，数组的值是这个前缀的最长可以匹配前缀子串的结尾字符下标。

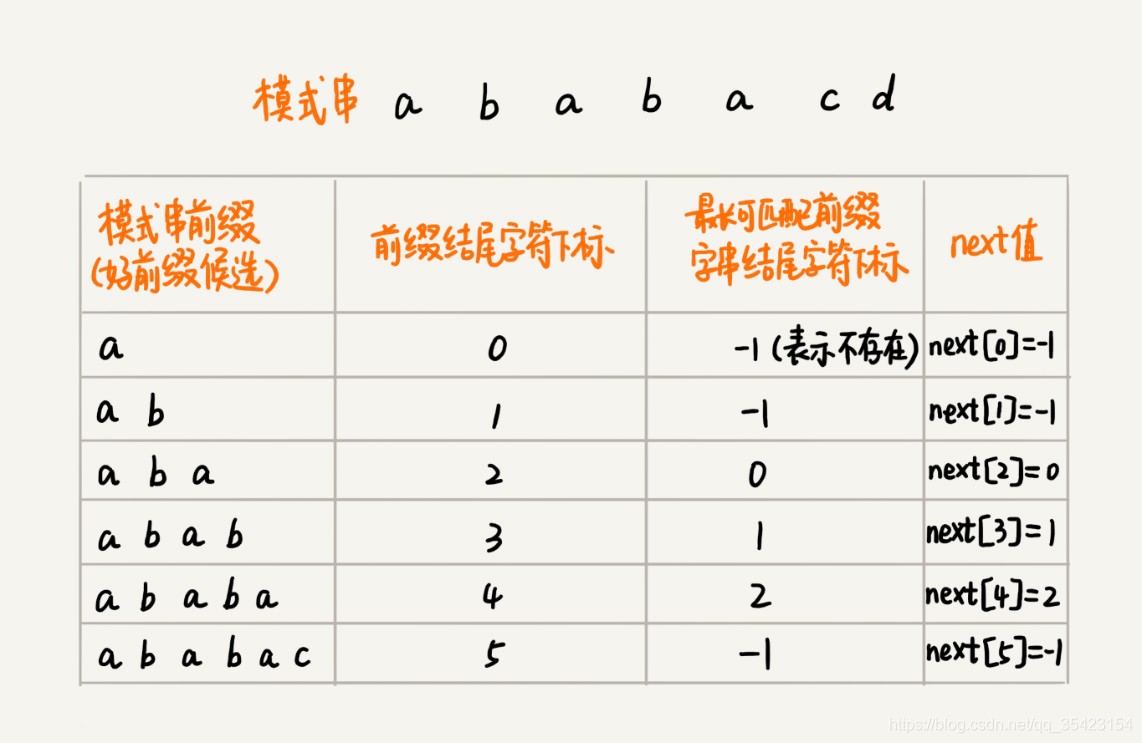
那么要如何构建next数组呢?我们需要借助到动态规划和回溯的思想，在大部分算法书和博客中都将这块描述的十分复杂，下面我就将其分解成多个问题，来方便理解

next数组构建时存在以下两种情况，为了方便表述，我将后缀起点定为i，前缀起点定为j

1. 前缀和后缀对应的位置匹配
2. 前缀和后缀对应的位置不匹配

前缀和后缀对应的位置匹配
由于第一个位置只有一个字符，不存在前缀和后缀一说，所以初值为-1，其他位置全部初始化为0。从第一个位置开始遍历。

我们可以采用动态规划的方法，如果当前位置的前缀和后缀匹配时，则匹配前缀的长度加一，而我们当前的前缀[0, i]又是从[0, i - 1]推导而来，所以它们之间的关系也就是next[i] = next[i - 1] + 1。

简而言之，如果当前的字符匹配，则当前next的值为上一个位置的值加一。

前缀和后缀对应的位置不匹配
假设此时已匹配前缀为GTGTGC，此时GTGT与GTGC中的T和C并不相同，又如何处理呢？

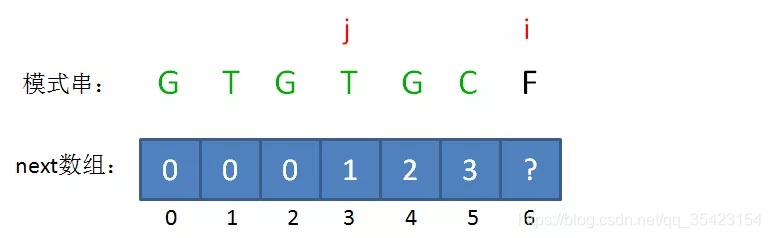
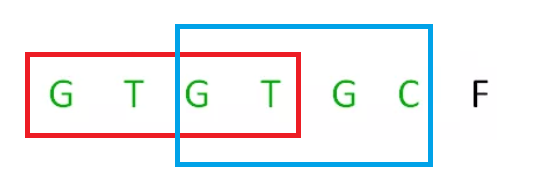
此时我们无法从上一个位置来推出这一个位置的值，而在这个坏字符出现之前，GTG又是一组可匹配的最长前缀子串，所以我们可以将问题GTGTGC转换为求后缀GTGC的最长可匹配前缀

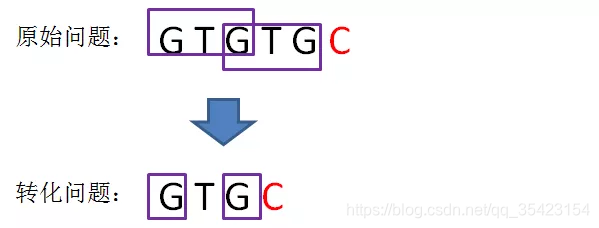
也就是将j给回溯到next[j]的位置

但是由于T和C还是不相同，所以再求后缀GC的最长可匹配前缀

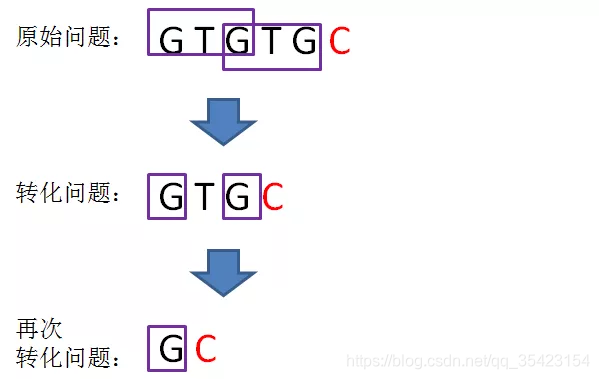
此时继续回溯

由于G不等于C，所以该位置没有任何匹配的前缀，next为0

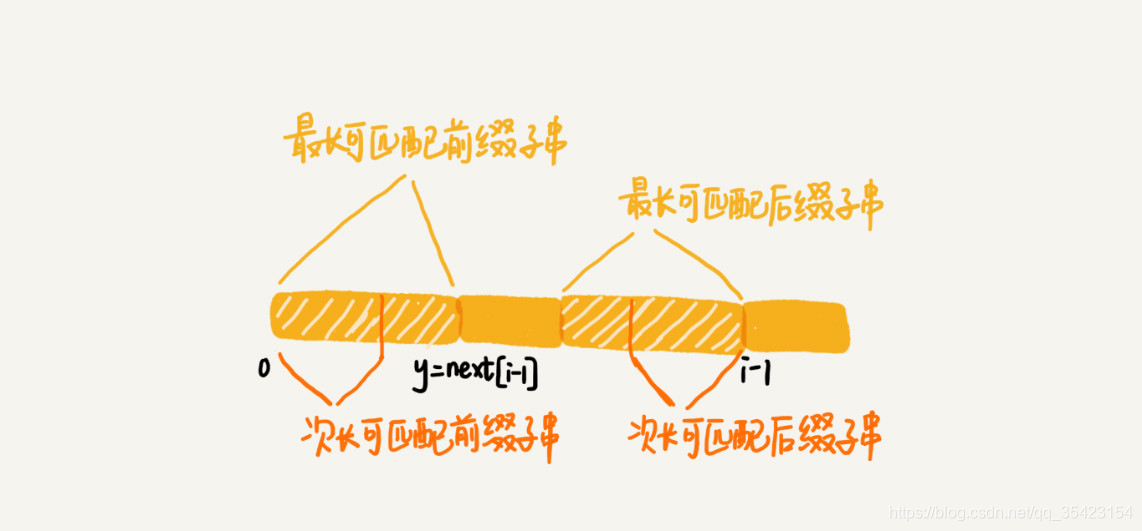
简而言之，如果最长可匹配后缀子串无法与前缀匹配，则尝试寻找当前的后缀子串中是否存在一个可匹配的前缀子串，将j回溯到next[j]的位置

void getNext(const string& pattern, vector<int>& next)
{int i , j = 0;next[0] = -1;   //第一个位置不存在数据，为-1for(int i = 1; i < next.size(); i++){//如果当前位置没有匹配前缀，则回溯到求当前后缀的最长可匹配前缀while(j != 0 && pattern[j] != pattern[i]){j = next[j];}//如果该位置匹配，则在next数组在上一个位置的基础上加一if(pattern[j] == pattern[i]){j++;}next[i] = j;}
}

代码实现

KMP的完整实现如下

#include
#include
#includeusing namespace std;//获取next数组
void getNext(const string& pattern, vector<int>& next)
{int i , j = 0;next[0] = -1;   //第一个位置不存在数据，为-1for(int i = 1; i < next.size(); i++){//如果当前位置没有匹配前缀，则回溯到求当前后缀的最长可匹配前缀while(j != 0 && pattern[j] != pattern[i]){j = next[j];}//如果该位置匹配，则在next数组在上一个位置的基础上加一if(pattern[j] == pattern[i]){j++;}next[i] = j;}
}int knuthMorrisPratt(const string& str, const string& pattern)
{//不满足条件则直接返回falseif(str.empty() || pattern.empty() || str.size() < pattern.size()){return -1;}int i = 0, j = 0;int len1 = str.size(), len2 = pattern.size();vector<int> next(pattern.size(), -1);   //next数组表示第j - 1个位置的匹配前缀的起始下标getNext(pattern, next);for(int i = 0; i < len1; i++){//找到最长的可匹配前缀while(j > 0 && str[i] != pattern[j]){j = next[j - 1] + 1;    //直接滑动到匹配的前缀位置，并继续匹配下一个位置}//如果匹配成功，则继续匹配下一个位置if(str[i] == pattern[j]){j++;}if(j == len2){return i - len2 + 1;    //返回主串中匹配子串的起始下标}}return -1;
}

空间复杂度
KMP算法需要借助到一个next数组，所以空间复杂度为O(M)，M为模式串长度
时间复杂度
时间复杂度主要包含两个部分，next数组的构建以及对主串的遍历。
其中next数组构建的时间复杂度可以估算为O(M)，第二步主串的循环为O(N)。所以KMP算法的时间复杂度为O(N + M)，N为主串长度，M为模式串长度

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！