[loj2087][NOI2016]国王饮水记

前言

回归OI，随便找一道清真dp题写写吧
做完发现一点都不清真

题目相关

链接

题目大意

现在有$n$个数，每次可以取若干个数，将每个数赋成平均值，限制$k$次，问第一个数最大能变成多少

数据范围

n≤1000,k≤109n\le1000,k\le10^9n≤1000,k≤109
另外，精度要求$p$位，$3\le p\le 3000$

题解

设$n$个数为h1,h2,h3⋅⋅⋅hnh_1,h_2,h_3···h_nh1​,h2​,h3​⋅⋅⋅hn​

• 对于$\forall i\in [2,n]$满足hi≤h1h_i\le h_1hi​≤h1​，这个数肯定不会被使用

这个很好证明，hih_ihi​与大于h1h_1h1​的数取平均只会让那些数变小，不优，hih_ihi​与小于等于h1h_1h1​的数取平均不会让他们变得大于h1h_1h1​

• 每次取平均一定是包含h1h_1h1​的

由于上一条我们已知，取平均的一定比h1h_1h1​大，那就有
h1+h2+h322<h1+h2+h33\frac{h_1+\frac{h_2+h_3}2}2<\frac{h_1+h_2+h_3}32h1​+2h2​+h3​​​<3h1​+h2​+h3​​
（因为h1<h2,h1<h3h_1<h_2,h_1<h_3h1​<h2​,h1​<h3​）

• 使用完一个数后，这个数将不会再被使用

根据取平均的性质，再根据第一条可得

• 如果次数足够多，那一定是从小到大一个个一次与h1h_1h1​取平均的

h1+h22+h32>h1+h2+h33\frac{\frac{h_1+h_2}2+h_3}2>\frac{h_1+h_2+h_3}322h1​+h2​​+h3​​>3h1​+h2​+h3​​
（h1<h2<h3h_1<h_2<h_3h1​<h2​<h3​）
所以大于$n$的$k$都是没用的，下文的$k$的数据范围均可当作小于等于$n$

然后就是次数不够多的情况，我们发现有些要合并
考虑dp
fi,jf_{i,j}fi,j​表示用了前$i$个数，进行了$j$次取合并的最大值
fi,j=max{max{(fk,j−1+∑l=k+1ihl)/(i−k+1)},fi−1,j}f_{i,j}=max\{max\{(f_{k,j-1}+\sum_{l=k+1}^ih_l)/(i-k+1)\},f_{i-1,j}\}fi,j​=max{max{(fk,j−1​+l=k+1∑i​hl​)/(i−k+1)},fi−1,j​}
不能忘记与fi−1,jf_{i-1,j}fi−1,j​取max，因为在次数不够的时候，并不一定所有数都要取
此处复杂度为O(n2kp)\mathcal O(n^2kp)O(n2kp)的，显然不能通过
把$\sum$改成前缀和相减的形式
设si=∑j=1ihjs_i=\sum_{j=1}^ih_jsi​=∑j=1i​hj​
fi,j=max{max{(fk,j−1+si−sk)/(i−k+1)},fi−1,j}f_{i,j}=max\{max\{(f_{k,j-1}+s_i-s_k)/(i-k+1)\},f_{i-1,j}\}fi,j​=max{max{(fk,j−1​+si​−sk​)/(i−k+1)},fi−1,j​}
把j这一维提掉
newfi=max{max{(fk+si−sk)/(i−k+1)},newfi−1}newf_i=max\{max\{(f_k+s_i-s_k)/(i-k+1)\},newf_{i-1}\}newfi​=max{max{(fk​+si​−sk​)/(i−k+1)},newfi−1​}
调整
newfi=max{max{(si−(sk−fk))/(i−(k−1))},newfi−1}newf_i=max\{max\{(s_i-(s_k-f_k))/(i-(k-1))\},newf_{i-1}\}newfi​=max{max{(si​−(sk​−fk​))/(i−(k−1))},newfi−1​}
变成斜率的形式
当前点(i,si)(i,s_i)(i,si​)要找一个点(k−1,sk−fk)(k-1,s_k-f_k)(k−1,sk​−fk​)使得他到我斜率最大
一个好想的方法是动态维护凸包，然后三分即可复杂度O(n2lognp)\mathcal O(n^2lognp)O(n2lognp)
事实上不需要三分，我们发现，如果新的斜率比上一个劣，是可以直接max上上一个的，由于每次询问的横坐标都增加了，如果更新了答案一定是在上次的决策右边

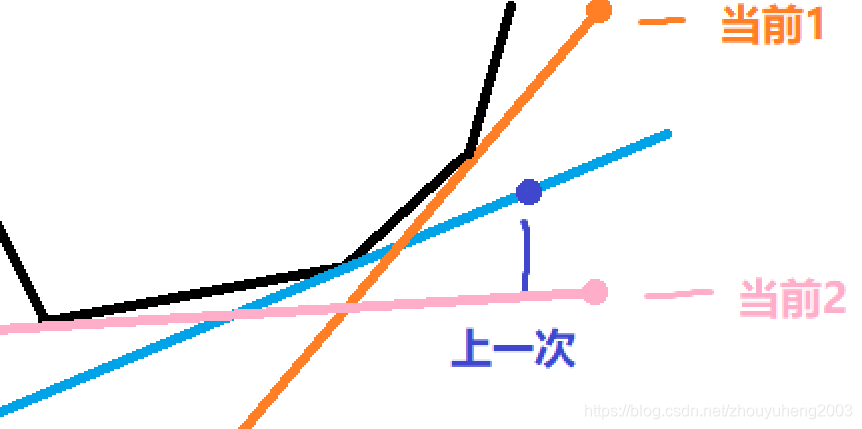
如图如果是当前2的情况，斜率是没有上一次优的，如果是当前1的情况，决策一定是在右边
所以此处有决策单调性，不需要三分
目前复杂度为O(n2p)\mathcal O(n^2p)O(n2p)

• 最优答案的转移过程中的$i-k$是单调不增的

比如
x+x12+x2+x33<x+x1+x23+x32\frac{\frac{x+x_1}{2}+x_2+x_3}{3}<\frac{\frac{x+x_1+x_2}{3}+x_3}{2}32x+x1​​+x2​+x3​​<23x+x1​+x2​​+x3​​
(x<x1<x2<x3)(x<x_1<x_2<x_3)(x<x1​<x2​<x3​)
一般化：
x+x1+⋅⋅⋅+xk−1k+xk+⋅⋅⋅+xnn−k+2<x+x1+⋅⋅⋅+xkk+1+xk+1+⋅⋅⋅+xnn−k+1\frac{\frac{x+x_1+···+x_{k-1}}{k}+x_k+···+x_n}{n-k+2}<\frac{\frac{x+x_1+···+x_k}{k+1}+x_{k+1}+···+x_n}{n-k+1}n−k+2kx+x1​+⋅⋅⋅+xk−1​​+xk​+⋅⋅⋅+xn​​<n−k+1k+1x+x1​+⋅⋅⋅+xk​​+xk+1​+⋅⋅⋅+xn​​
(x<x1<x2<x3⋅⋅⋅<xn,k<n−k+1)(x<x_1<x_2<x_3···<x_n,k<n-k+1)(x<x1​<x2​<x3​⋅⋅⋅<xn​,k<n−k+1)
证明：
先由条件得到$2k\le n$
全部通分
(n−k+1)(x+x1+⋅⋅⋅+xk−1+k(xk+⋅⋅⋅+xn))<(n−k+2)(x+x1+⋅⋅⋅+xk+(k+1)(xk+1+⋅⋅⋅+xn))(n-k+1)(x+x_1+···+x_{k-1}+k(x_k+···+x_n))<(n-k+2)(x+x_1+···+x_k+(k+1)(x_{k+1}+···+x_n))(n−k+1)(x+x1​+⋅⋅⋅+xk−1​+k(xk​+⋅⋅⋅+xn​))<(n−k+2)(x+x1​+⋅⋅⋅+xk​+(k+1)(xk+1​+⋅⋅⋅+xn​))
移项（+式子美化）
0<x+∑i=1k−1xi+(n−k+2−(n−k+1)k)xk+((n−k+2)(k+1)−(n−k+1)k)(∑i=k+1nxi)0<x+\sum_{i=1}^{k-1}x_i+(n-k+2-(n-k+1)k)x_k+((n-k+2)(k+1)-(n-k+1)k)\left(\sum_{i=k+1}^nx_i\right)0<x+i=1∑k−1​xi​+(n−k+2−(n−k+1)k)xk​+((n−k+2)(k+1)−(n−k+1)k)(i=k+1∑n​xi​)
0<x+∑i=1k−1xi+(n−2k+2−nk+kk)xk+(n+2)(∑i=k+1nxi)0<x+\sum_{i=1}^{k-1}x_i+(n-2k+2-nk+kk)x_k+(n+2)\left(\sum_{i=k+1}^nx_i\right)0<x+i=1∑k−1​xi​+(n−2k+2−nk+kk)xk​+(n+2)(i=k+1∑n​xi​)
x+∑i=1k−1xi+(n−2k+2−nk+kk)xk+(n+2)(∑i=k+1nxi)>x+∑i=1k−1xi+(n−2k+2−nk+kk)xk+(n+2)(n−k)xkx+\sum_{i=1}^{k-1}x_i+(n-2k+2-nk+kk)x_k+(n+2)\left(\sum_{i=k+1}^nx_i\right)>x+\sum_{i=1}^{k-1}x_i+(n-2k+2-nk+kk)x_k+(n+2)(n-k)x_kx+i=1∑k−1​xi​+(n−2k+2−nk+kk)xk​+(n+2)(i=k+1∑n​xi​)>x+i=1∑k−1​xi​+(n−2k+2−nk+kk)xk​+(n+2)(n−k)xk​
······根据xk<xk+1<⋅⋅⋅<xnx_k<x_{k+1}<···<x_nxk​<xk+1​<⋅⋅⋅<xn​
x+∑i=1k−1xi+(n−2k+2−nk+kk)xk+(n+2)(n−k)xk>(n−2k+2−nk+kk)xk+(n+2)(n−k)xkx+\sum_{i=1}^{k-1}x_i+(n-2k+2-nk+kk)x_k+(n+2)(n-k)x_k>(n-2k+2-nk+kk)x_k+(n+2)(n-k)x_kx+i=1∑k−1​xi​+(n−2k+2−nk+kk)xk​+(n+2)(n−k)xk​>(n−2k+2−nk+kk)xk​+(n+2)(n−k)xk​
·····根据$x>0$减去一些正数会变小
(n−2k+2−nk+kk)xk+(n+2)(n−k)xk=(nn−2k+2n−nk+n−2k+2−nk+kk)xk=(n(n−k)−k(n−k)+2n−4k+n+2)>0(n-2k+2-nk+kk)x_k+(n+2)(n-k)x_k=(nn-2k+2n-nk+n-2k+2-nk+kk)x_k=(n(n-k)-k(n-k)+2n-4k+n+2)>0(n−2k+2−nk+kk)xk​+(n+2)(n−k)xk​=(nn−2k+2n−nk+n−2k+2−nk+kk)xk​=(n(n−k)−k(n−k)+2n−4k+n+2)>0
······根据$2k\le n,n>0$可得
至此证毕

• 最优答案的转移过程中$i-k>1$的段数仅有O(lognhΔ)\mathcal O(log\frac{nh}{\Delta})O(logΔnh​)个，Δ=mini{hi−hi−1}\Delta=min_i\{h_i-h_{i-1}\}Δ=mini​{hi​−hi−1​}
  这个地方看了讲稿也不懂了（看了很久都没弄懂）
  
  
  贴个讲稿的link
  这样就只转移14次
  此处有会证明的教教我啊
  最后复杂度的话就是O(nplognhΔ)\mathcal O(nplog\frac{nh}{\Delta})O(nplogΔnh​)

代码

然后还要使用高精小数板子

代码先鸽一会儿，很快就来

总结

体验好差233

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！