小数问题

本文的主要内容是探讨关于小数的一些问题，先介绍小数与分数的转化，然后再来探讨小数循环节等问题。其中涉及

到一些数论的内容，本文会进行详细介绍。

题目：http://acm.hdu.edu.cn/showproblem.php?pid=1717

题意：给定一个纯小数，将其转化为分数输出。

代码：

#include 
#include 
#include using namespace std;
const int N = 15;int gcd(int a, int b)
{return b ? gcd(b, a % b) : a;
}void DecimalToFraction(char str[])
{int a = 0;int b = 0;int L1 = 0;int L2 = 0;int len = strlen(str);for(int i = 2; i < len; i++){if(str[i] == '(') break;a = a * 10 + str[i] - '0';L1++;}bool flag = 0;for(int i = 2; i < len; i++){if(str[i] == '(' || str[i] == ')'){flag = 1;continue;}b = b * 10 + str[i] - '0';L2++;}L2 -= L1;int p = b - a;int q = 0;if(!flag){p = b;q = 1;L2 = 0;}for(int i = 0; i < L2; i++)q = q * 10 + 9;for(int i = 0; i < L1; i++)q = q * 10;int g = gcd(p, q);p /= g;q /= g;printf("%d/%d\n", p, q);
}int main()
{int T;char str[N];scanf("%d", &T);while(T--){scanf("%s", str);DecimalToFraction(str);}return 0;
}

题目：http://acm.hdu.edu.cn/showproblem.php?pid=2522

题意：给定一个分数，将其转化为小数。本题需要用到如下定理

代码：

#include 
#include 
#include using namespace std;
const int N = 100005;void FractionToDecimal(int n)
{//负数标识bool isNeg = 0;if(n < 0){n = -n;isNeg = 1;}int res[N], ok[N];memset(res, 0, sizeof(res));memset(ok, 0, sizeof(ok));int k = 1;ok[k] = 1;int cnt = 0;while(k && n != 1){k *= 10;res[cnt++] = k / n;k %= n;if(ok[k]) break;ok[k] = 1;}if(isNeg) printf("-");if(n == 1) puts("1");else{printf("0.");for(int i = 0; i < cnt; i++)printf("%d", res[i]);puts("");}
}int main()
{int T, n;scanf("%d", &T);while(T--){scanf("%d", &n);FractionToDecimal(n);}return 0;
}

题目：http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1037

题意：求小于等于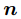的数中倒数循环节长度最长的那个数，其中。

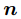
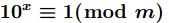
分析：从上题的定理看，我们需要在小于等于的数中找一个数，使得同余方程的最小正

     整数解最大。很明显，此方程的最大正整数解为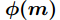，如果10为模的一个原根，那么将得到方程的最

     小正整数解为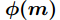，这时得到的循环节当然也就最长。

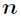
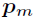
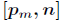
     设小于等于且原根为10的最大的素数为。接下来，看似只需要枚举闭区间内的每个数，找

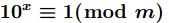
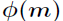
     出满足同余方程的最小正整数解为的所有数，然后取循环节长度最大的那个。

     但是遗憾的是，枚举的数可能比较多，而且每次枚举都需要解同余方程，时间花费很多。实际上只需要枚举

     原根存在的。根据数论原根中的一个定理

     根据上题的定理知道，肯定不含有2，所以只需要枚举形如的数即可。

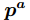
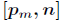
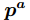
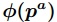
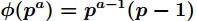
     我们要在闭区间内找形如且原根为10的所有。如果原根为10，那么同余方程的最小正整数解

     为，也就是小数循环节的长度，在数论欧拉函数章节中，学过。

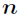
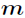
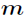
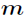
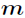
     综上所述，本题思路为：从开始往下枚举，直到为素数且10为模的一个原根时停止，判断是

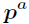
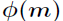
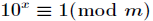
     否形如，如果是，进一步验证是否是的最小正整数解，最终取循环节长度最大

     的。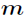

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include const int Times = 10;
const int N = 1000005;using namespace std;
typedef long long LL;bool prime[N];
int p[N];
int cnt;LL gcd(LL a, LL b)
{return b? gcd(b, a % b) : a;
}LL multi(LL a, LL b, LL m)
{LL ans = 0;a %= m;while(b){if(b & 1){ans = (ans + a) % m;b--;}b >>= 1;a = (a + a) % m;}return ans;
}LL quick_mod(LL a, LL b, LL m)
{LL ans = 1;a %= m;while(b){if(b & 1){ans = multi(ans, a, m);b--;}b >>= 1;a = multi(a, a, m);}return ans;
}bool Miller_Rabin(LL n)
{if(n == 2) return true;if(n < 2 || !(n & 1)) return false;LL m = n - 1;int k = 0;while((m & 1) == 0){k++;m >>= 1;}for(int i = 0; i < Times; i++){LL a = rand() % (n - 1) + 1;LL x = quick_mod(a, m, n);LL y = 0;for(int j = 0; j < k; j++){y = multi(x, x, n);if(y == 1 && x != 1 && x != n - 1) return false;x = y;}if(y != 1) return false;}return true;
}LL pollard_rho(LL n, LL c)
{LL i = 1, k = 2;LL x = rand() % (n - 1) + 1;LL y = x;while(true){i++;x = (multi(x, x, n) + c) % n;LL d = gcd((y - x + n) % n, n);if(1 < d && d < n) return d;if(y == x) return n;if(i == k){y = x;k <<= 1;}}
}void find(LL n, int c, vector &pri)
{if(n == 1) return;if(Miller_Rabin(n)){pri.push_back(n);return ;}LL p = n;int k = c;while(p >= n) p = pollard_rho(p, c--);find(p, k, pri);find(n / p, k, pri);
}void Divide(LL n, vector &pri, vector &num)
{find(n, 120, pri);sort(pri.begin(), pri.end());num.push_back(1);int k = 1;for(int i = 1; i < pri.size(); i++){if(pri[i] == pri[i - 1])++num[k - 1];else{num.push_back(1);pri[k++] = pri[i];}}pri.resize(num.size());
}void SearchFactor(int dept, LL ans, vector &pri, vector &num, vector &fac)
{if(dept == num.size()){fac.push_back(ans);return;}for(int i = 0; i <= num[dept]; i++){SearchFactor(dept + 1, ans, pri, num, fac);ans *= pri[dept];}
}vector FindFactor(LL n)
{int cnt;vector pri;vector num;vector fac;Divide(n, pri, num);SearchFactor(0, 1, pri, num, fac);sort(fac.begin(), fac.end());return fac;
}//素数筛选
void PrimeFilter()
{cnt = 0;memset(prime, true, sizeof(prime));for(int i = 2; i < N; i++){if(prime[i]){p[cnt++] = i;for(int j = i + i; j < N; j += i)prime[j] = false;}}
}bool Judge(LL m, LL &phi, bool &isprime)
{// p^1if(Miller_Rabin(m)){phi = m - 1;isprime = true;return true;}//p^2LL srt = (LL)sqrt(1.0 * m);if(srt * srt == m && Miller_Rabin(srt)){phi = srt * (srt - 1);return true;}//p^3, p^4, ...LL tm = m;LL fm = 1;for(int i = 0; i < cnt; i++){if(tm % p[i] == 0){fm = p[i];while(tm % p[i] == 0){tm /= p[i];fm *= p[i];}if(tm == 1){phi = fm - fm / p[i];return true;}break;}}return false;
}bool Success(LL m, LL &loop, bool &ok)
{LL phi = 0;bool isprime = false;if(!Judge(m, phi, isprime))return false;LL res = 0;vector fac = FindFactor(phi);for(int i = 0; i < fac.size(); i++){if(quick_mod(10, fac[i], m) == 1){res = fac[i];break;}}if(res != phi)return false;loop = phi;if(isprime)ok = true;return true;
}int main()
{LL n;PrimeFilter();while(scanf("%I64d", &n) != EOF){n++;bool ok = 0;LL ans = 0;LL res = 0;while(n--){LL loop = 0;if(Success(n, loop, ok)){if(ans < loop){ans = loop;res = n;}if(ok){printf("%I64d\n", res);break;}}}}return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！