cp分解实现_如何用贝叶斯高斯张量分解修复缺失数据？(Jupyter notebook - Python)

本文来源于BGCP Imputation - transdim，主要讨论如何利用贝叶斯高斯张量分解(Bayesian Gaussian CP decomposition, BGCP) 估计矩阵中的缺失元素，其中，贝叶斯概率矩阵分解是以高斯分布为基本假设，并采用Gibbs采样做参数估计。另外，感兴趣的读者可在transdim - GitHub项目中下载数据集和Jupyter notebook。

准备阶段

在进行贝叶斯高斯张量分解之前，需要调用一些常用的package，如numpy等。以scipy.stats中的Wishart分布和numpy.random中的多元正态分布为基础，设计贝叶斯高斯张量分解采样过程中会遇到的Gaussian-Wishart分布。

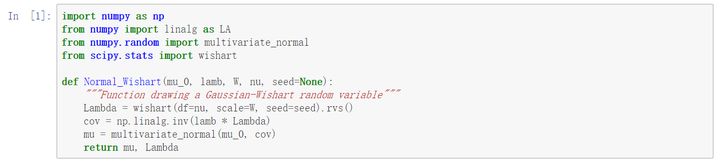
另外，在矩阵分解过程中，为了加快采样过程的计算效率，需要用到一种特殊的矩阵运算规则 - Khatri-Rao积，即

Khatri-Rao积的函数 (kr_prod) 和实例：

定义CP分解的组合结构 (cp_combination)：

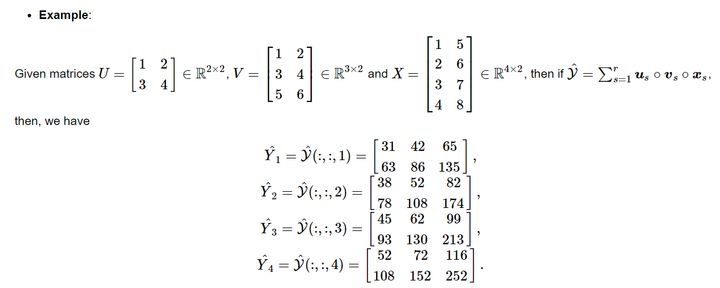
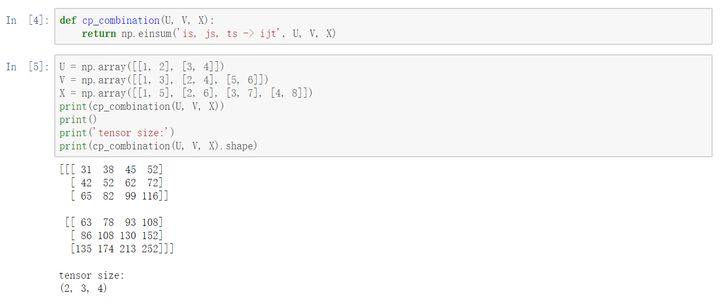
定义张量展开（将张量展开成矩阵, ten2mat）：

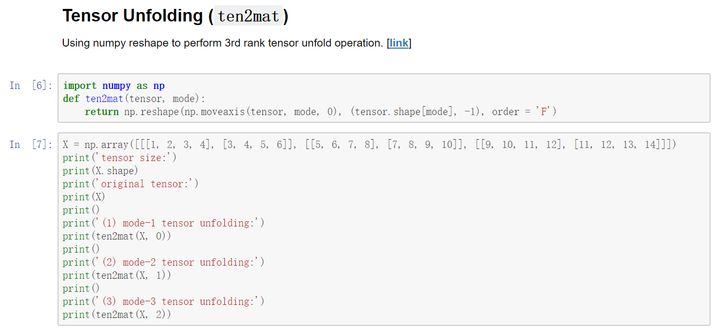
贝叶斯高斯张量分解原理

张量元素被假设服从高斯分布，为了求解矩阵分解的隐性因子矩阵，依据贝叶斯准则，需进一步对模型参数和超参数设置共轭先验。具体如下：

在所设计的贝叶斯网络中，对模型参数和超参数求后验分布，交替更新即可完成贝叶斯高斯张量分解。

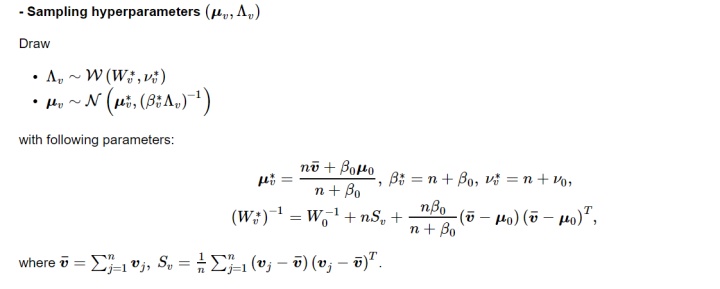
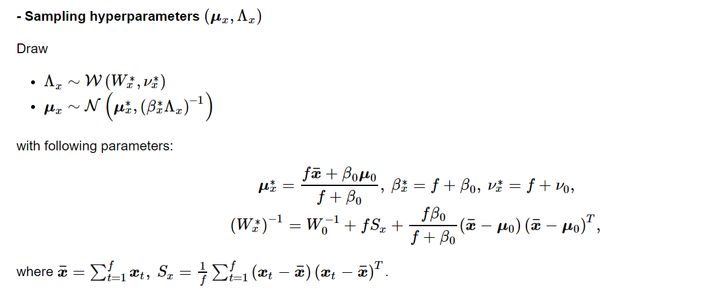
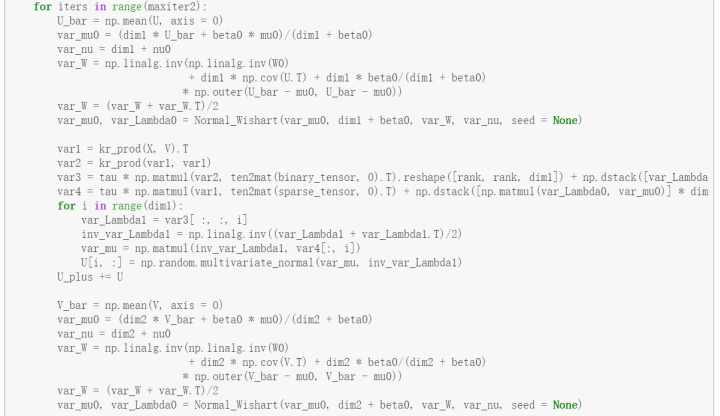
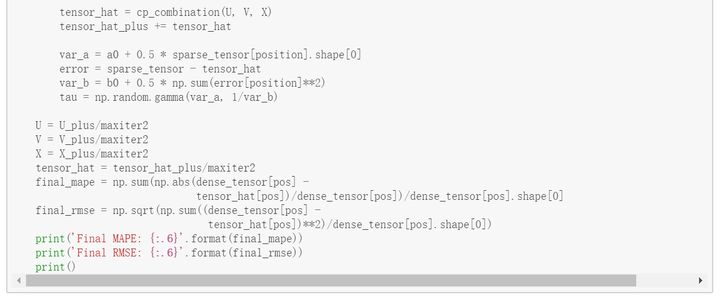
编译实现贝叶斯高斯张量分解的Python代码：

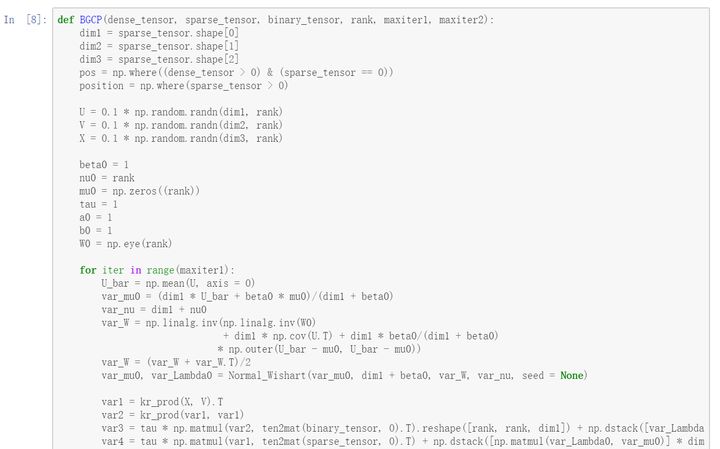
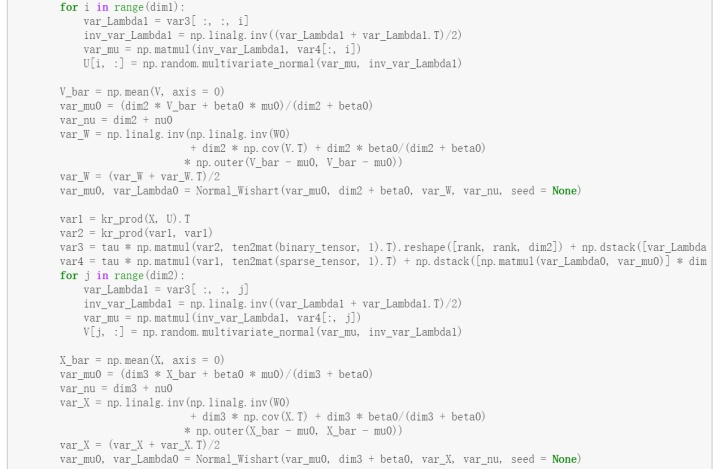
缺失数据修复实验

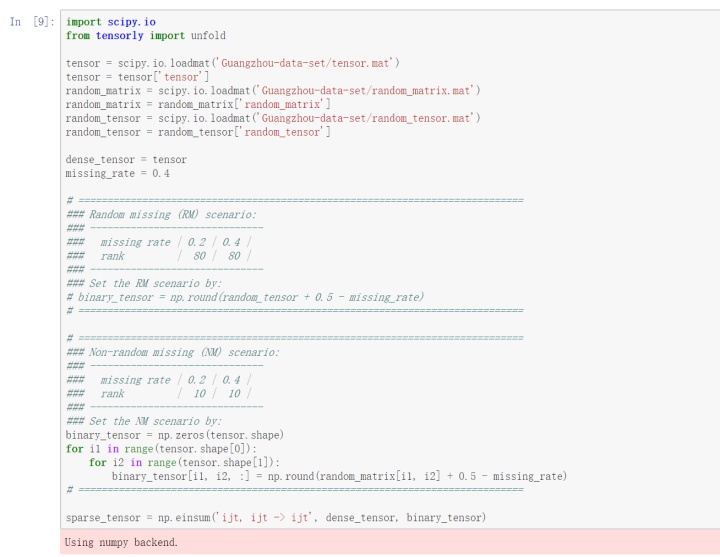
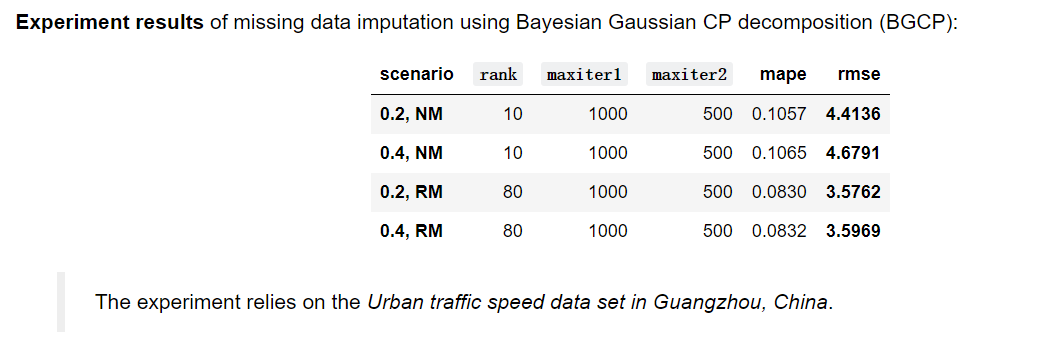
以广州路网车速数据集为基础，设计面向时空交通数据的缺失值修复实验。

数据集下载链接1：https://github.com/xinychen/transdim/tree/master/Guangzhou-data-set
数据集下载链接2：Urban Traffic Speed Dataset of Guangzhou, China

主要参考

BGCP Matlab代码：https://github.com/lijunsun/bgcp_imputation

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！