GFocal解读

总的来说，GFocal这篇文章的数学性还是很高的，如果对此不感兴趣，可以阅读原作者的《大白话 Generalized Focal Loss》。

简介

众所周知，单阶段检测器的发展是目标检测领域的重要研究方向，而单阶段方法往往将目标检测视为密集分类和定位任务（其中定位任务值得就是边框回归）。分类任务通常通过Focal Loss进行优化，而边框定位通常按照Dirac delta分布来学习。最近单阶段检测器的研究趋势为引入一个单独的分支来估计定位的质量（centerness或者iou），这个质量预测有助于分类任务的进行从而整体上提高检测的性能。GFocal这篇文章就是针对上述的三个表示（representation）进行的工作，分别是分类表示、定位表示和检测框的质量估计，这里的表示指的是检测器最终的输出也就是head的输出。这三种表示一般关系如下图所示。

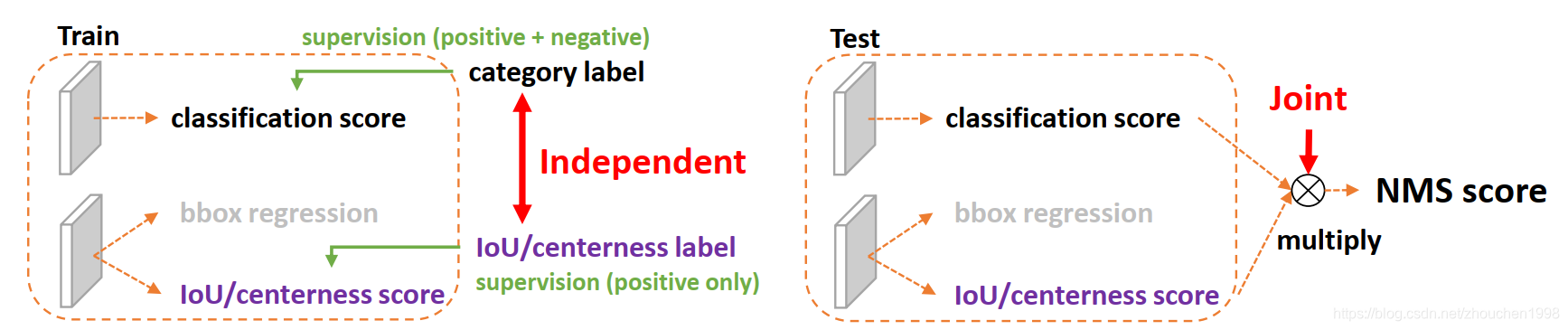
作者发现目前的表示学习有两个问题，第一，质量估计和分类训练和推理时时不一致的（两个分支单独训练，但是推理时乘在一起，如上图所示）；第二，Dirac delta分布的定位表示不够灵活，无法建模复杂场景下的歧义和不确定性。

为了解决这两个问题，论文作者设计了新的表示方式，将质量评估合并到分类预测向量中形成一个联合进行定位质量评估和分类的表示，此外也使用一个向量来表示任意的概率分布，这个概率分布用来建模边框位置信息（也就是说，边框回归的输出从定值变为了一个概率分布）。这两个方案可以有效解决上述的问题，特别是提出的联合表示可以有效消除不一致问题，但是因此标签也变为了连续值，因此作者提出对离散值的focal loss的扩展，即论文的Generalized Focal Loss （GFL），成功推广到了连续域上。在COCO数据集上，同等backbone和训练设置下，GFocal获得了0.45的AP，超越了SAPD和ATSS，而GFocal有着更快的速度。这文章最终收录在NeurIPS2020。

• 论文标题

  Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection

• 论文地址

  http://arxiv.org/abs/2006.04388

• 论文源码

  https://github.com/implus/GFocal

介绍

近年来，密集检测器逐渐引领了目标检测的发展趋势，而对于边框表示和定位质量估计的研究也有了不错的进展。在过去数年中，边框表示被建模为简单的Dirac delta分布。FCOS中提出了一个额外的定位质量估计分支（使用center ness得分或者iou得分），这为检测的准确性带来了不小的提高，但是，在推理时质量估计和分类分支是组合到一起（通过乘法）作为NMS排序的置信度的。尽管有了很大的成功，但是论文作者发现了现有方法存在的一些问题。

1. 质量估计和分类得分在训练和推理时的使用不一致

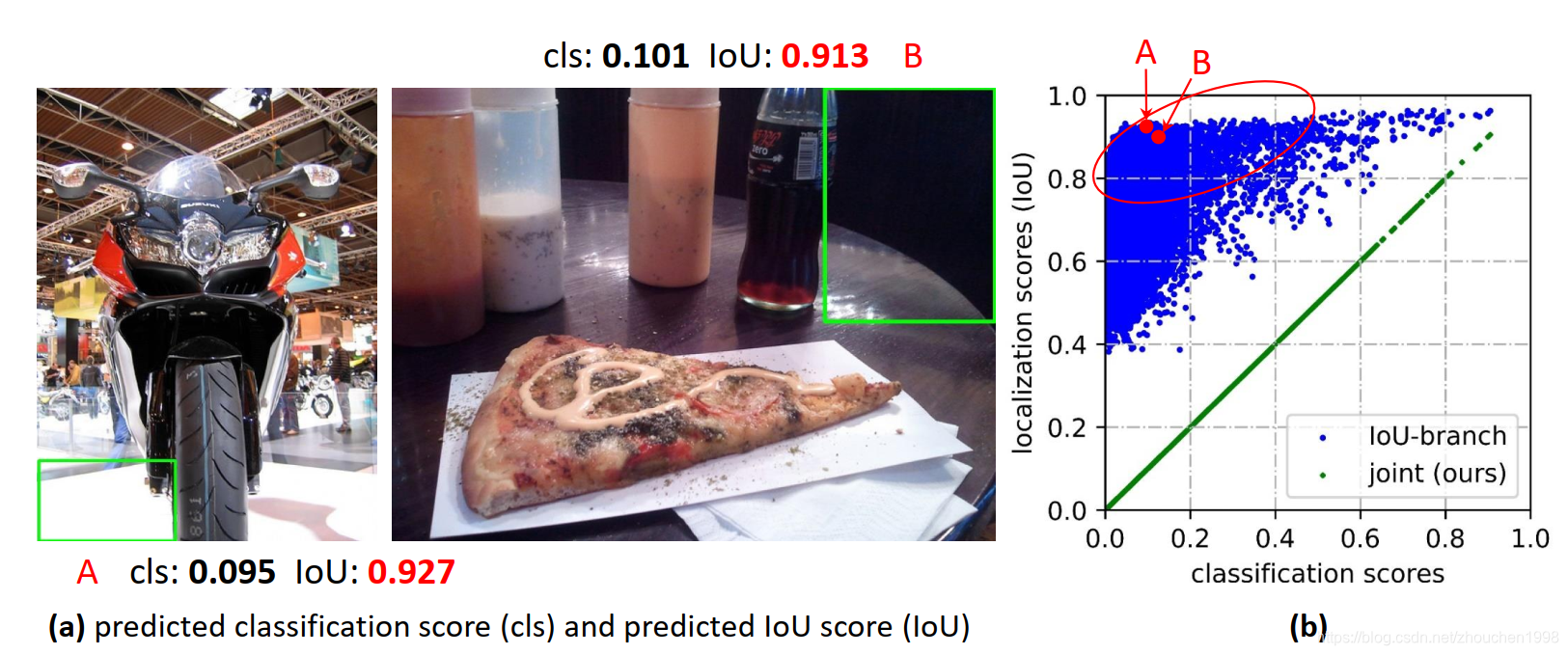
如上图(a)所示，在密集预测检测器中，定位质量评估和分类得分时分别训练的，但是推理时却是组合使用的。还有就是，定位质量评估的监督只对正样本进行，这是不可靠的，因为有些负样本也可能获得较高的质量得分（因为它们时没有监督的，所以负样本的质量预测时模型不了解的未定义行为），而这个不合理的高质量评估得分和很低的分类得分乘起来后用于NMS排序，可能使得这些负样本排到正样本前面，这当然是很不合理的（示例如下图(a)所示）。

2. 边界框表示不灵活

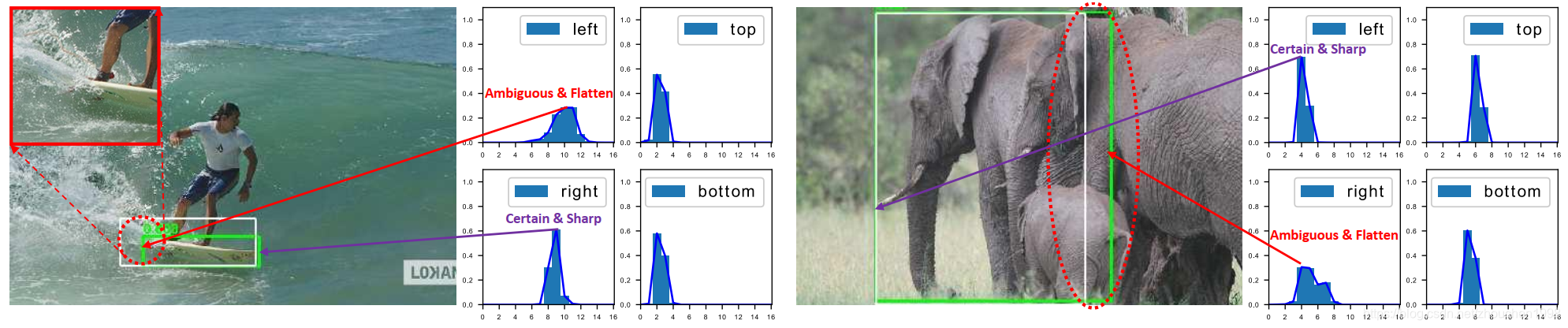
常用的边界框表示的方法可以认为是狄拉克分布，但是实际场景中目标的标注框往往具有歧义和不确定性，比如下图所示的不清晰的边界（被水模糊的滑板和严重遮挡的大象），狄拉克这种简单分布式难以建模的。后来诞生了一些方法采用高斯分布来建模边框，但是高斯分布还没有复杂到足以捕获目标框的位置分布，因为真实的分布可能是任意且灵活的，不需要高斯分布那样对称。

为了解决上述的两个问题，GFocal设计了新的边界框表示方法和新的定位质量估计表示。对于定位质量的表示，作者提出将其和分类得分进行合并得到一个统一的表示，而对于边界框的表示，作者则将其建模为连续空间上的概率分布（论文称为General distribution），下文详细。理解这两个思路。

方法

方案

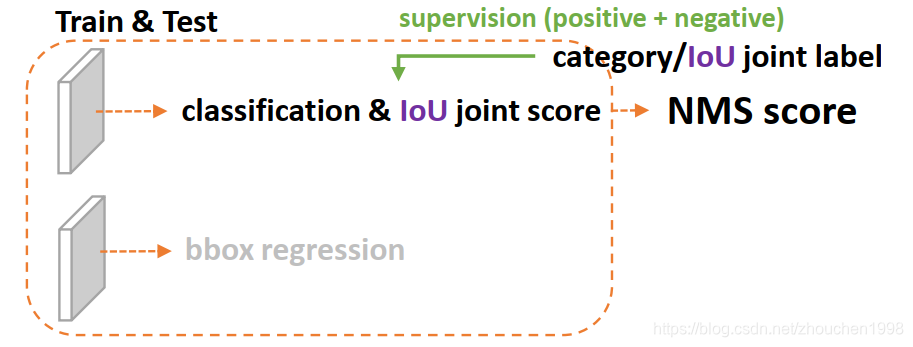
上文说到，作者为了解决定位质量表示和分类得分表示不一致的问题，作者将定位质量融入到了分类得分中形成一个统一的表示向量，该向量GT类别下标处对应的置信度不再是分类置信度而是质量预测的得分（这个得分一般采用预测框和真实框的IoU来表示）。将这个统一的表示记为classification-IoU joint representation，它可以被端到端优化且在推理时直接使用，如下图所示。这种方法可以有效消除训练和测试的不一致并且建模了分类和质量评估之间的强相关性。进一步看，由于在分类分支中，因此负样本也会被监督（质量得分为0），使得质量评估更加可靠。

对于边框的表示，作者提出用任意分布来建模边界框并在连续空间上直接学习概率分布，不引入如高斯分布那样较强的先验知识。这里其实简单理解就是，原本FCOS等方法预测中心点到边界的距离是一个值（狄拉克分布），而论文预测的时中心点到边界的概率分布向量。这种方法可以有效进行边框回归，同时感知边框的潜在分布。

具体方法

方案出来了，接下来就是要面对的问题了，首先看第一个方案，此时其实预测的标签已经从离散的{0,1}变为了连续的0-1的，而Focal Loss是不支持离散标签的，它的公式可以简单表述如下（忽略原始论文的αt\alpha_tαt​）。

FL(p)=−(1−pt)γlog⁡(pt),pt={p,when y=11−p,when y=0\mathbf{F L}(p)=-\left(1-p_{t}\right)^{\gamma} \log \left(p_{t}\right), p_{t}=\left\{\begin{aligned} p, & \text { when } y=1 \\ 1-p, & \text { when } y=0 \end{aligned}\right. FL(p)=−(1−pt​)γlog(pt​),pt​={p,1−p,​ when y=1 when y=0​

这个公式中的y∈{1,0}y \in \{1,0\}y∈{1,0}表示真实类别，而$p\in [0,1]$表示估计的标签为$y=1$的概率，$\gamma$是可以调整的聚焦参数。具体来看，Focal loss由一个标准交叉熵的部分−log⁡(pt)-\log \left(p_{t}\right)−log(pt​)和动态缩放因子部分(1−pt)γ\left(1-p_{t}\right)^{\gamma}(1−pt​)γ组成，这个缩放因子可以在训练时对容易样本降权而使得模型快速聚焦难样本的学习。

然而，对于分类质量的联合表示，标签已经变为了0-1的连续值，具体说，此时$y=0$表示质量得分为0的负样本，而$0<y\le 1$代表目标IoU标签为$y$的正样本，为了解决这个问题，作者对Focal Loss的两个部分分别进行了扩展以保证可以在联合表示下使用。首先，原来的交叉熵部分−log⁡(pt)-\log \left(p_{t}\right)−log(pt​)被修改为完整的形式$-((1-y)\log (1-\sigma )+y\log (\sigma ))$；接着，缩放因子部分(1−pt)γ\left(1-p_{t}\right)^{\gamma}(1−pt​)γ被推广到预测的sigmoid结果和连续标签$y$的绝对距离，即∣y−σ∣β(β≥0)|y-\sigma|^{\beta}(\beta \geq 0)∣y−σ∣β(β≥0)，两侧的绝对值确保非负。将这两个拓展部分组合到一起，形成完整的Quality Focal Loss（QFL），公式如下。

QFL(σ)=−∣y−σ∣β((1−y)log⁡(1−σ)+ylog⁡(σ))\mathbf{Q F L}(\sigma)=-|y-\sigma|^{\beta}((1-y) \log (1-\sigma)+y \log (\sigma)) QFL(σ)=−∣y−σ∣β((1−y)log(1−σ)+ylog(σ))

和Focal Loss类似，魔改后的调制因子也有关注难样本的功能，当预测的质量估计值与真实标签相差很多的时候，∣y−σ∣β|y-\sigma|^{\beta}∣y−σ∣β的值便较大，模型就能更关注于这些难分类的样本；而当预测值与真实标签很接近的时候，损失便也接近0，所以简单样本的损失权重便被降低了。

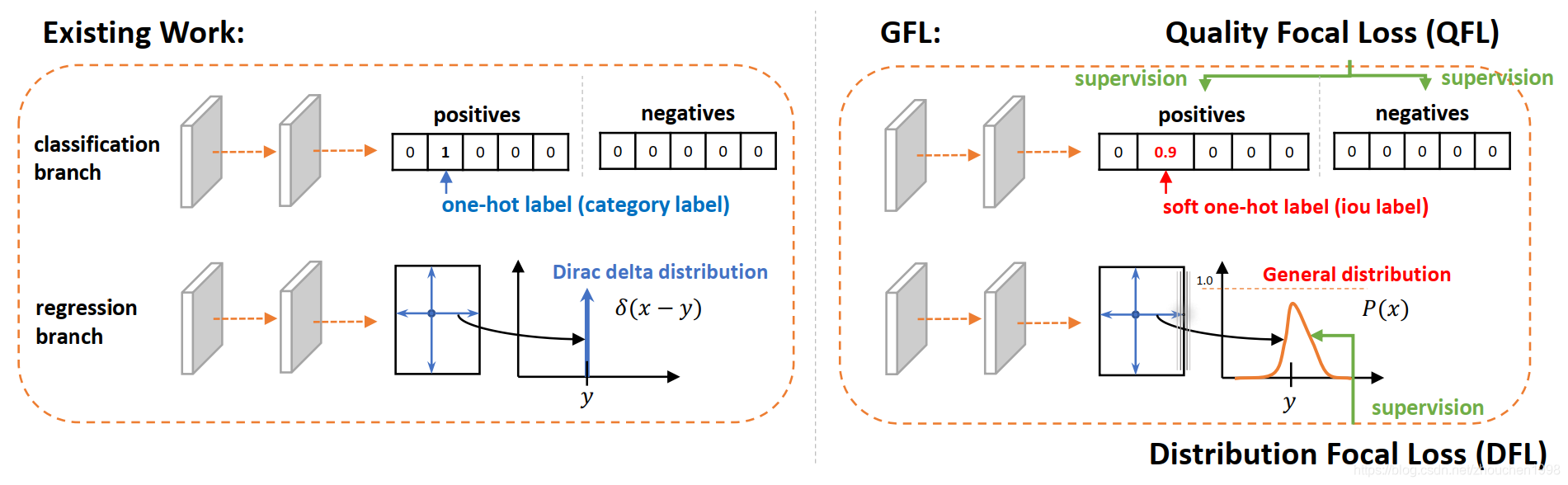
上如右侧的上半部分就是上面提到的QFL，下半部分就是我们后面要讲的DFL。

我们接着看，作者如何解决第二个方案遇到的问题，这篇文章采用的边框回归的目标是中心点到四个边的相对偏移，如上图所示的回归分支（采用哪种回归目标其实大同小异）。如上图左侧的回归分支所示，传统的边框回归是将标签$y$建模为狄拉克分布，也就是只有一个值概率为一，说的更通俗易懂就是只会产生一个输出值（比如到左边框的偏移是$x$），通常通过全连接层实现。作者认为应该不引入先验直接建模一个通用分布$P(x)$，也就是预测值是一个概率分布，可以理解为中心点到边的概率（因而由四个概率向量）。

假定标签$y$的最小值为y0y_0y0​最大值为yny_nyn​（y0≤y≤yn,n∈N+y_{0} \leq y \leq y_{n}, n \in \mathbb{N}^{+}y0​≤y≤yn​,n∈N+），而模型预测的y^\hat{y}y^​则可以通过预测的概率分布得到（这里y^\hat{y}y^​同样满足y0≤y^≤yny_{0} \leq \hat{y} \leq y_{n}y0​≤y^​≤yn​），计算式如下。需要补充的是，实际上代码实现是，作者是将y0y_0y0​设置为0，yny_nyn​设置为16的。

y^=∫−∞+∞P(x)xdx=∫y0ynP(x)xdx\hat{y}=\int_{-\infty}^{+\infty} P(x) x \mathrm{~d} x=\int_{y_{0}}^{y_{n}} P(x) x \mathrm{~d} x y^​=∫−∞+∞​P(x)x dx=∫y0​yn​​P(x)x dx

为了适配卷积神经网络，作者将连续域上的积分转换为离散表示，具体是将区间[y0,yn]\left[y_{0}, y_{n}\right][y0​,yn​]离散化为集合{y0,y1,…,yi,yi+1,…,yn−1,yn}\left\{y_{0}, y_{1}, \ldots, y_{i}, y_{i+1}, \ldots, y_{n-1}, y_{n}\right\}{y0​,y1​,…,yi​,yi+1​,…,yn−1​,yn​}，集合每个元素间隔为了简单取1。此时有∑i=0nP(yi)=1\sum_{i=0}^{n} P\left(y_{i}\right)=1∑i=0n​P(yi​)=1，因而估计的回归值变为下式。$P(x)$可以通过Softmax函数实现，因此P(yi)P(y_i)P(yi​)可以记作SiS_iSi​。

y^=∑i=0nP(yi)yi\hat{y}=\sum_{i=0}^{n} P\left(y_{i}\right) y_{i} y^​=i=0∑n​P(yi​)yi​

注意，因为已经得到了y^\hat{y}y^​，因此它可以使用L1损失、IoU损失或者GIoU损失来训练，但是作者分析了一下发现一个积分目标可能对于无数种积分模式（如下图的面积相同的三种分布，显然第三种最合适，因为最合适的位置如果存在那么与标签不会相差太远），这有损学习效率。考虑到真实的分布通常不会距离标注的位置太远，所以作者又额外加了个loss，希望网络能够快速地聚焦到标注位置附近的数值，使得他们概率尽可能大。

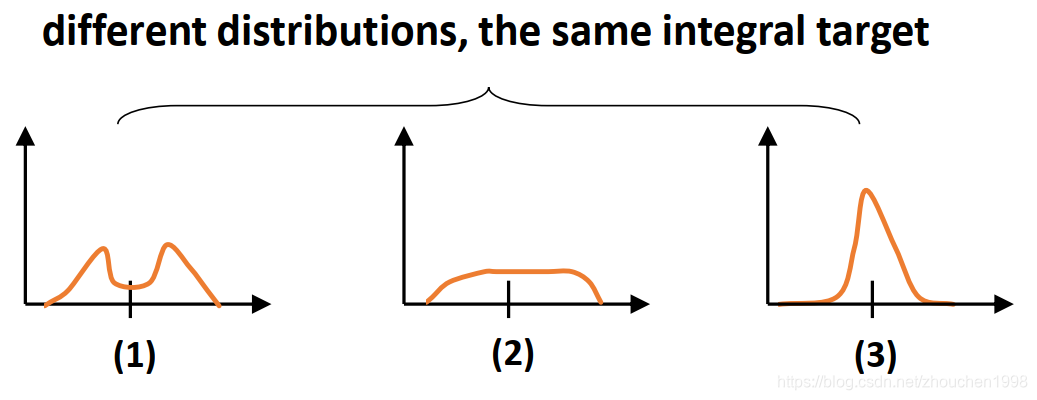
基于此，作者将这个损失取名Distribution Focal Loss (DFL) ，它显式增大最接近标签$y$的两侧的yiy_iyi​和yi+1y_{i+1}yi+1​的概率。此外，由于边框回归只考虑正样本没有不平衡问题的风险，简单将QFL的完整交叉熵部分应用过来就行，形成的DFL公式如下。公式中关于SiS_iSi​和Si+1S_{i+1}Si+1​如何能够接近目标，作者在论文补充材料进行了证明，这里不多赘述。

DFL(Si,Si+1)=−((yi+1−y)log⁡(Si)+(y−yi)log⁡(Si+1))\mathbf{D F L}\left(\mathcal{S}_{i}, \mathcal{S}_{i+1}\right)=-\left(\left(y_{i+1}-y\right) \log \left(\mathcal{S}_{i}\right)+\left(y-y_{i}\right) \log \left(\mathcal{S}_{i+1}\right)\right) DFL(Si​,Si+1​)=−((yi+1​−y)log(Si​)+(y−yi​)log(Si+1​))

最后，其实归纳可以发现，QFL和DFL可以表示为一个通用的形式，也就是本文的标题由来Generalized Focal Loss (GFL)，我这里就简单给出这个公式，诸多细节可以阅读原论文。

GFL(pyl,pyr)=−∣y−(ylpyl+yrpyr)∣β((yr−y)log⁡(pyl)+(y−yl)log⁡(pyr))\mathbf{G F L}\left(p_{y_{l}}, p_{y_{r}}\right)=-\left|y-\left(y_{l} p_{y_{l}}+y_{r} p_{y_{r}}\right)\right|^{\beta}\left(\left(y_{r}-y\right) \log \left(p_{y_{l}}\right)+\left(y-y_{l}\right) \log \left(p_{y_{r}}\right)\right) GFL(pyl​​,pyr​​)=−∣y−(yl​pyl​​+yr​pyr​​)∣β((yr​−y)log(pyl​​)+(y−yl​)log(pyr​​))

训练损失

最终的训练损失如下式，其中LQ\mathcal{L}_{\mathcal{Q}}LQ​表示QFL而LD\mathcal{L}_{\mathcal{D}}LD​表示DFL，而LB\mathcal{L}_{\mathcal{B}}LB​指的是GIoU Loss，NposN_{pos}Npos​表示正样本数目，λ0\lambda_{0}λ0​和λ1\lambda_1λ1​是LQ\mathcal{L}_{\mathcal{Q}}LQ​和LD\mathcal{L}_{\mathcal{D}}LD​的平衡权重。在金字塔特征图的所有位置计算求和。这里的1{cz∗>0}\mathbf{1}_{\left\{c_{z}^{*}>0\right\}}1{cz∗​>0}​为指示函数，当cz∗>0c_{z}^{*}>0cz∗​>0时为1，否则为0。

L=1Npos ∑zLQ+1Npos ∑z1{cz∗>0}(λ0LB+λ1LD)\mathcal{L}=\frac{1}{N_{\text {pos }}} \sum_{z} \mathcal{L}_{\mathcal{Q}}+\frac{1}{N_{\text {pos }}} \sum_{z} \mathbf{1}_{\left\{c_{z}^{*}>0\right\}}\left(\lambda_{0} \mathcal{L}_{\mathcal{B}}+\lambda_{1} \mathcal{L}_{\mathcal{D}}\right) L=Npos ​1​z∑​LQ​+Npos ​1​z∑​1{cz∗​>0}​(λ0​LB​+λ1​LD​)

实验

作者进行了一些消融实验，这里就不细说了，这里直接说明两个结论。

1. QFL和DFL两个损失的作用是正交的，他们的增益互不影响，所以结合使用会有更好的效果。
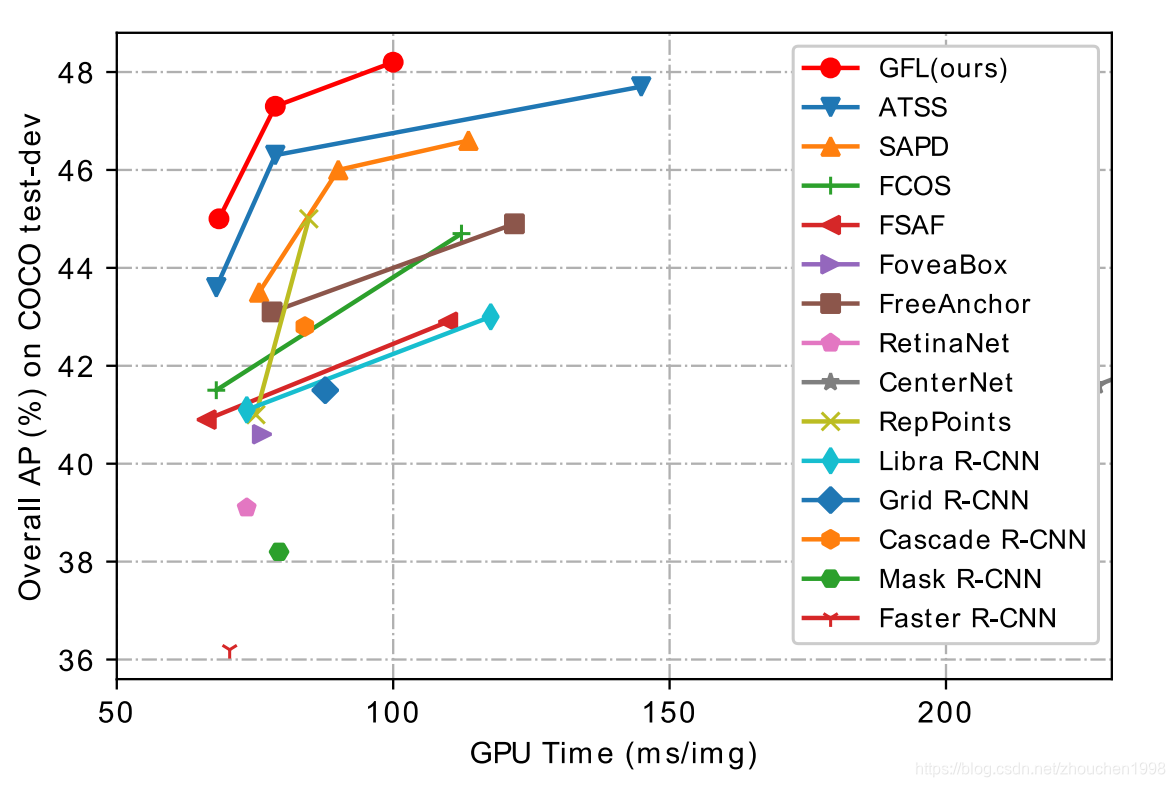
2. GFocal与各大模型相比，取得了较为不错的speed-accuracy trade-off，基本上属于无痛涨点的利器。

下图是单模型单尺度的结果对比，可以看到，GFocal取得了相当亮眼的表现。

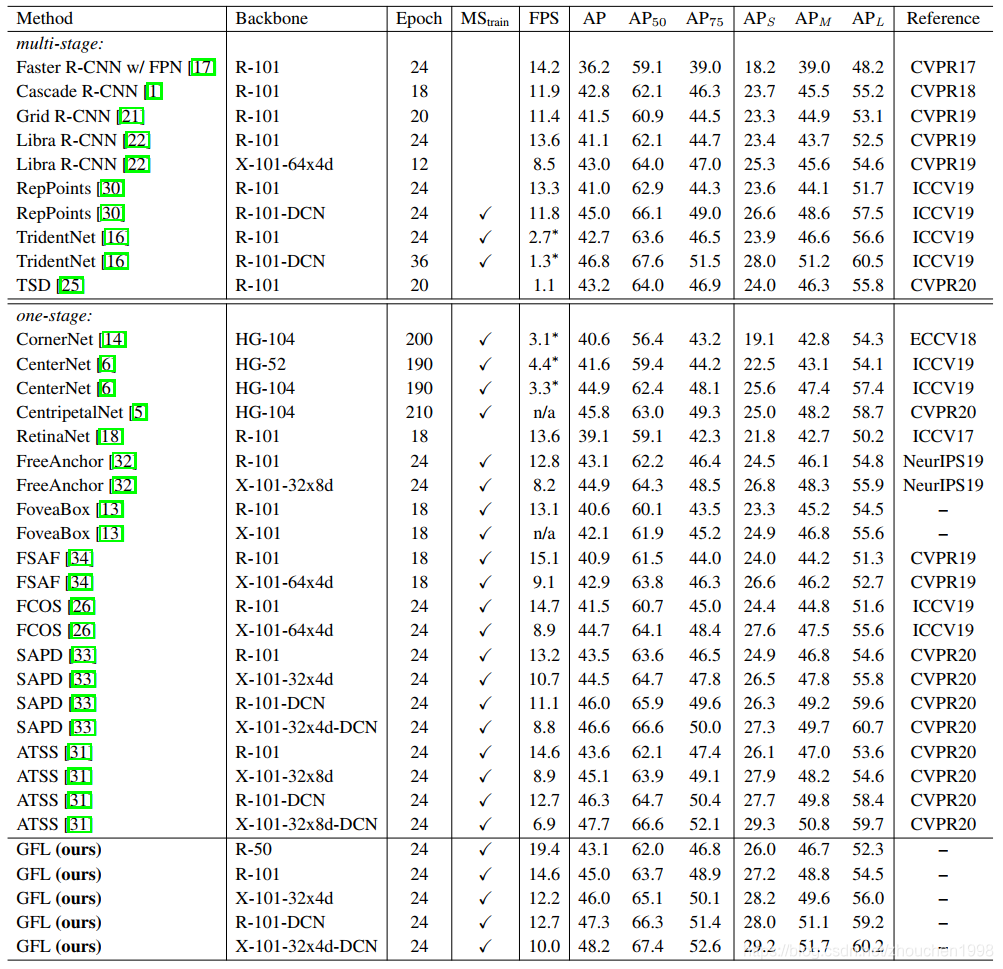
此外，也附上和SOTA对比的实验结果图。

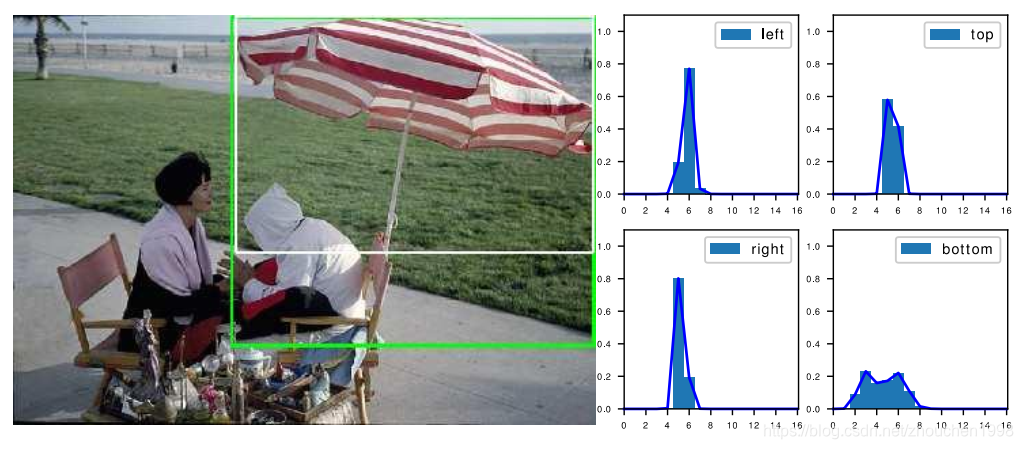
文章的补充材料也有不少干货，关于centerness和IoU的对比我就不赘述了，此外作者也进行了分布式边框表示的可视化，以下图为例，可视化四个边的预测分布，可以发现一个有趣的现象，当伞不算伞柄也就是白色GT框可以定位伞，但是算上伞兵绿色预测框又可以定位伞，概率分布也得确是一个双峰分布，这其实表达标注和模型对某个物体的两种理解，这个双峰分布很有趣，给后来的研究留下了无数遐想。

总结

这篇文章从表示（representation）这一模型学习的关键出发提出了GFocal，将边框建模为概率表示极具开创性。论文基于mmdetection实现，也很便于源码的阅读和使用，是相当亮眼的工作，值得一读。最后，本文我只是做了一些基本的解读，更详细的请参考原论文，如果我的文章对你有所帮助，欢迎一键三连，你的支持是我不懈创作的动力。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！