回溯法经典例题--任务分配问题--C语言

问题描述：

        有n个任务需要分配给n个人执行，每个任务只能分配给一个人，每个人只能执行一个任务，第i个人执行第j个任务的成本是c【i】【j】。求出总成本最小的一种方案。

求解：

        任务的选择依旧可以表示成一棵n叉树，每次父节点向孩子结点的延申，就是当前i号人员选择第j个任务。

         设计递归，当i递归到==n，说明所有人都选择了一个互相之间各不相同的任务，这便是出口，也是一次结果，用temp【】来记录本次人员的选择，用temp_cost来记录本次结果，misson【】数组保证每个任务只能被选择一次。

        设计剪枝，我们发现当走到某个非叶子节点后的temp_cost已经大于之前的结果了，我们可以把它剪掉。

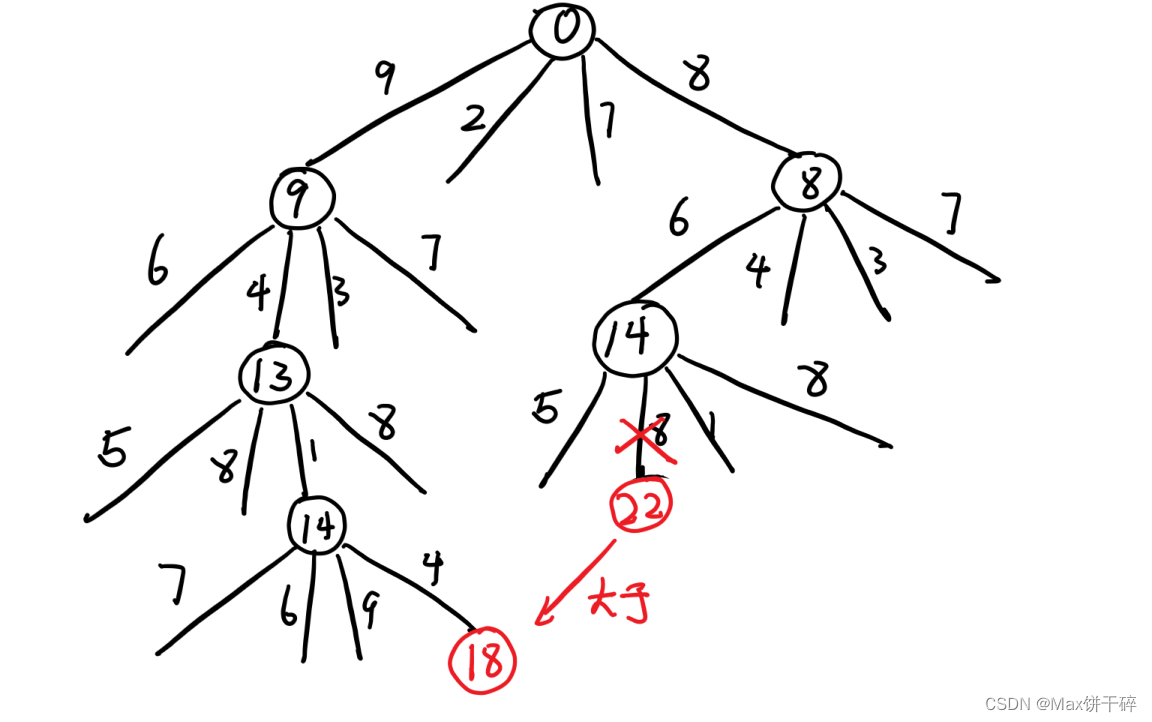
代码：

#include
#include
using namespace std;
#define max 10
int min_cost = 999;
void dis(int* x, int n) {for (int i = 0; i < n; i++)cout << x[i] << " ";cout << endl;
}
bool check_mission(int* mission, int n) {for (int i = 0; i < n; i++) {if (mission[i] == 0)return false;}return true;
}
void dfs(int c[max][max], int* mission, int* temp, int* x, int temp_cost,int n, int i) {if (i == n) {if (temp_cost < min_cost) {min_cost = temp_cost;for (int j = 0; j < n; j++)x[j] = temp[j];}}else {for (int j = 0; j < n; j++) {if (mission[j] == 0) {if (temp_cost+c[i][j] > min_cost)continue;temp[i] = j;mission[j] = 1;dfs(c, mission, temp, x, temp_cost + c[i][j],n, i + 1);mission[j] = 0;}}}
}int main() {int c[max][max] = { {9,2,7,8},{6,4,3,7},{5,8,1,8},{7,6,9,4} };int mission[max];int x[max];int temp[max];int n = 4;//一共四人个人，一共四种任务memset(temp, -1, sizeof(temp));memset(x, -1, sizeof(x));memset(mission, 0, sizeof(mission));int temp_cost = 0;dfs(c, mission, temp, x, temp_cost,n, 0);dis(x, n);return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！