调用 OR-Tools GLOP 求解器的简单模型实例

本文介绍 Python 语言调用 OR-Tools 求解器，求解线性规划模型和整数规划模型的代码示例。

线性规划模型 - Klee-Minty Cube

Klee-Minty Cube 问题：

代码示例：

from datetime import datetime
from ortools.linear_solver import pywraplpn = 100
epsilon = 0.1# instantiate a Glop solver
solver = pywraplp.Solver('klee_minty_cube', problem_type=pywraplp.Solver.GLOP_LINEAR_PROGRAMMING)# variables
x = [solver.NumVar(0, solver.infinity(), 'x_{}'.format(i)) for i in range(n)]# constraints
solver.Add(0 <= x[0])
solver.Add(x[0] <= 1)
for i in range(1, n):solver.Add(epsilon * x[i - 1] <= x[i])solver.Add(x[i] <= 1 - epsilon * x[i - 1])# objective
solver.Maximize(x[n - 1])# solve
dts = datetime.now()
status = solver.Solve()
dte = datetime.now()
tm = round((dte - dts).seconds + (dte - dts).microseconds / (10 ** 6), 3)
print("OR-Tools GLOP model solving time:  {} s".format(tm), '\n')# result
if status == pywraplp.Solver.OPTIMAL:print("solution:")obj_opt = solver.Objective().Value()print("objective value:  {}".format(obj_opt))list_x_res = [x[i].solution_value() for i in range(n)]print("x solution:  {}".format(list_x_res))
else:print("The problem does not have an optimal solution.")print("\nAdvanced usage:")
print("Problem solved in %f milliseconds" % solver.wall_time())
print("Problem solved in %d iterations" % solver.iterations())

参考资料：

The Glop Linear Solver

整数规划模型 - 选址问题

选址问题的整数规划模型较为经典，此处不赘述。

代码示例：

from datetime import datetime
from typing import List, Dictfrom ortools.linear_solver import pywraplpdef location(num_node: int, mat_distance: List[List[float]]) -> Dict[int, List[int]]:"""location model:param num_node:  nodes amount:param mat_distance:  distance matrix:return: dict_res:  {centre node: [node] list} dictionary"""# 整数规划模型 problem_type: CBC_MIXED_INTEGER_PROGRAMMINGsolver = pywraplp.Solver('location', problem_type=pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)x = [[solver.BoolVar('x_{}_{}'.format(i, j)) for j in range(num_node)] for i in range(num_node)]# 选址问题基本约束for j in range(num_node):solver.Add(sum(x[i][j] for i in range(num_node)) == 1)for i in range(num_node):solver.Add(x[i][j] <= x[i][i])# 约束：中心点的数量（聚类数量）solver.Add(sum(x[i][i] for i in range(num_node)) == 10)# 目标：最小化总距离solver.Minimize(sum(x[i][j] * mat_distance[i][j] for j in range(num_node) for i in range(num_node)))dts = datetime.now()status = solver.Solve()dte = datetime.now()tm = round((dte - dts).seconds + (dte - dts).microseconds / (10 ** 6), 3)print("OR-Tools GLOP model solving time:  {} s".format(tm), '\n')# case 1: 最优解dict_res = {}if status == pywraplp.Solver.OPTIMAL:print("solution:")obj_opt = solver.Objective().Value()  # 获取最优目标函数值print("objective value:  {}".format(round(obj_opt, 4)))mat_x_res = [[x[i][j].solution_value() for j in range(num_node)] for i in range(num_node)]  # 获取最优解for i in range(num_node):if mat_x_res[i][i] > 0.9:list_tmp = []for j in range(num_node):if mat_x_res[i][j] > 0.9:list_tmp.append(j)dict_res[i] = list_tmpprint("centre code {} serves nodes:  {}".format(i, list_tmp))# case 2: 无解elif status == pywraplp.Solver.INFEASIBLE:print("Model infeasible!")# case 3: 其他else:print("unexpected status:  {}.".format(status))print("\nAdvanced usage:")print("Problem solved in %f milliseconds." % solver.wall_time())  # 求解时间print("Problem solved in %d iterations." % solver.iterations())  # 迭代次数return dict_res

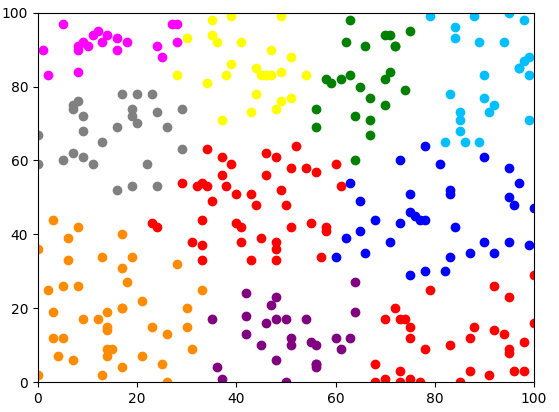
算例规模：300 个点，10 个选址中心

硬件配置：i7-8700 3.20GHz 3.19GHz CPU；16GB 内存

求解时间：12.159 s

结果可视化：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！