基于表格的RL：Q-learning、sarsa

value-based表格简介

state：有限个（离散）

action：有限个（离散）

里面的值 对应的是 当前state下，做这个action，价值是多少！

价值不仅仅与 当前状态state做完action拿到的reward有关，还与进入下一个状态state_拿到奖励的期望有关

马尔科夫

马尔科夫性

马尔可夫性质（英语：Markov property）是概率论中的一个概念，因为俄国数学家安德雷·马尔可夫得名[1]。当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态；换句话说，在给定现在状态时，它与过去状态（即该过程的历史路径）是条件独立的，那么此随机过程即具有马尔可夫性质。具有马尔可夫性质的过程通常称之为马尔可夫过程。

马尔科夫链

马尔可夫链（英语：Markov chain），又称离散时间马尔可夫链（discrete-time Markov chain，缩写为DTMC[1]），因俄国数学家安德烈·马尔可夫得名，为状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性”称作马尔可夫性质。马尔科夫链作为实际过程的统计模型具有许多应用。

马尔科夫决策过程MDP

要素包括状态S、动作A、状态转移概率P 和奖励R

P函数反映了环境的随机性，做出(s，a)之后，进入哪个s' 由P决定。

自己的总结

我处在当前的状态s，未来的状态只跟当前状态s有关，与之前的状态无关。

我处在当前状态s，我做什么动作a，都不需要考虑之前的状态。

近朱者赤近墨者黑

虽然我在state下做action得到的reward不高，甚至可能小负，比如-2，

但是我100%进入下一个好的状态 state_，在这个状态下 做任何reward都是+100的奖励，

那么我认为q（s,a） = -2 + gama * 100

 

在靠近done的位置state，做正确action得reward （比如+100），因为它done了，所以它的动作的价值就是获得的这个reward。

那么靠近final位置的 state，做进入这个state的action，得到reward （小） + gama * 100  

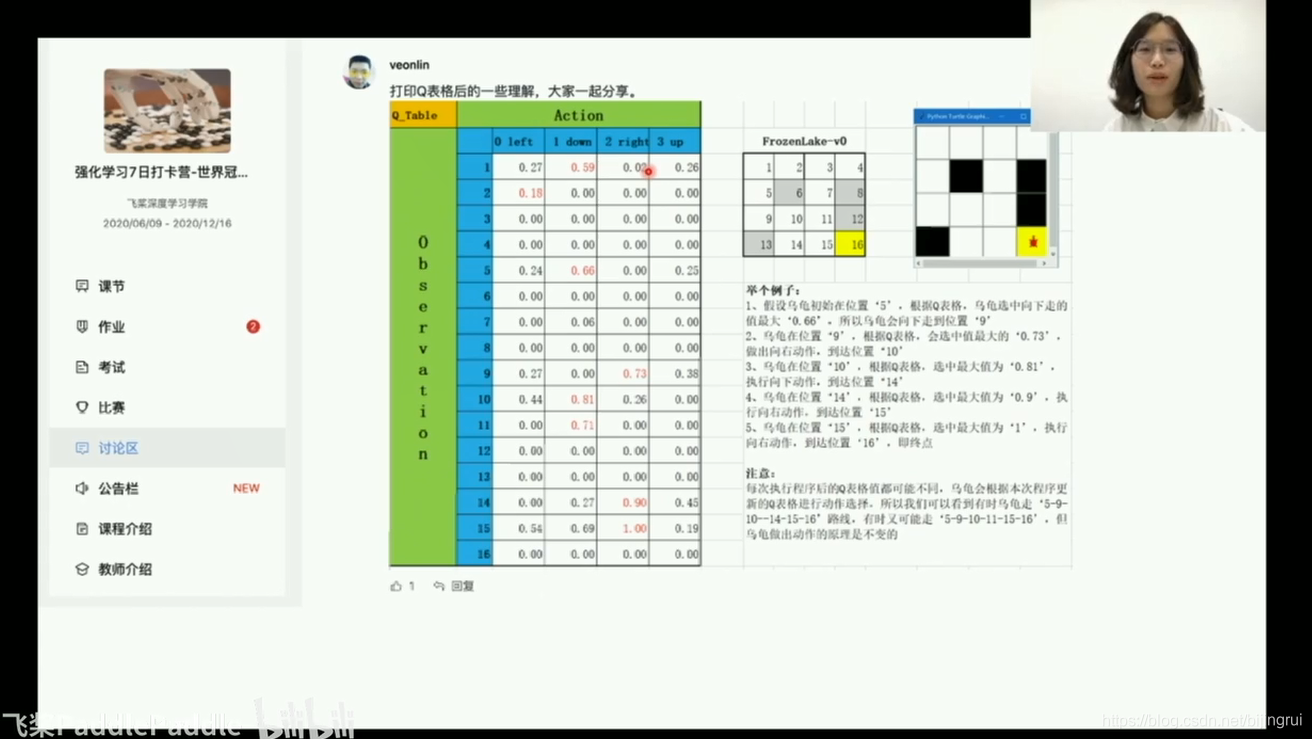
表格里的值 动作的价值  就是 discounted return！ 

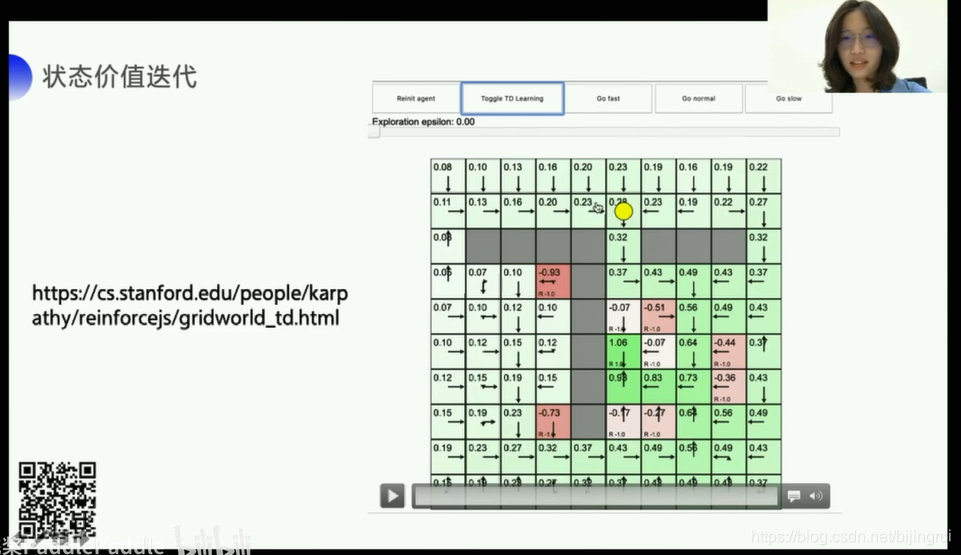
TD更新

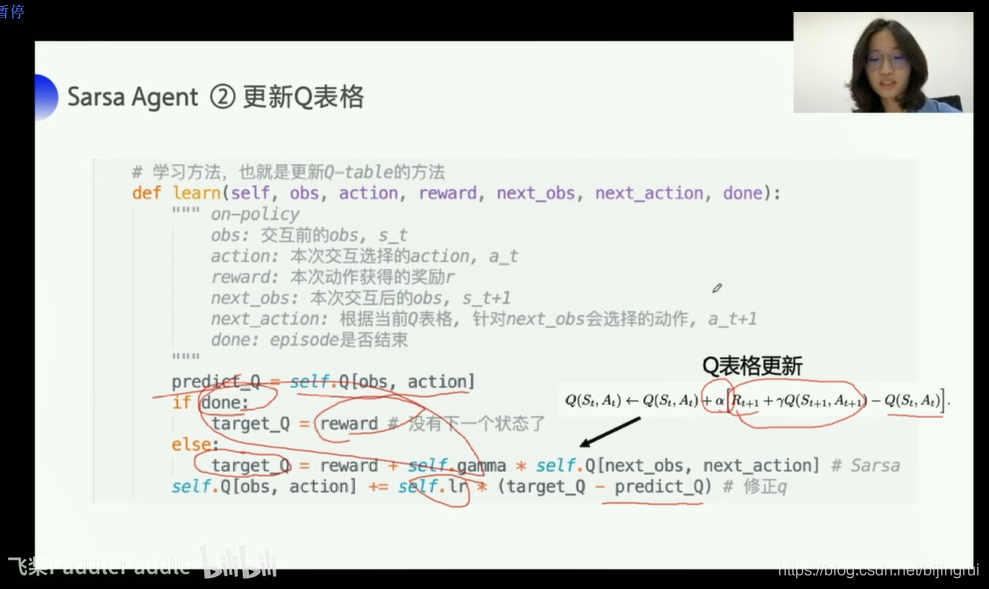
SARSA

名字来源

s a r s' a'

公式

 他是on-policy的策略，s a r s' a'都是自己亲自操作得来的经验

sample一个动作探索/选择最优动作去predict

Qlearning

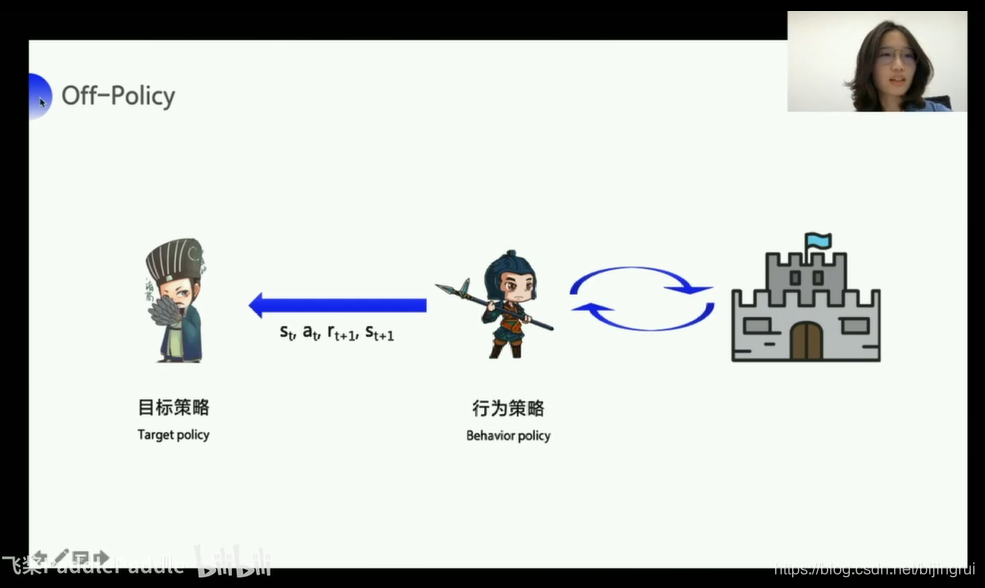
on-policy/off-policy

on policy

喂给的数据 是实实在在执行过的经验 是sarsa

off policy

喂给的数据 并不是sarsa 而是 sars' 并不需要 

在test_env，默认下一个action，就是predict的时候，选择value最大的action

在train_env ，下一个action是e-greedy探索的 action，比如90%是当前最优，10%是随机探索

为什么sarsa保守？

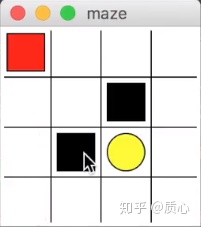
初始状态在左上角，目标奖励在黄色区域，黑色区域为惩罚。Q-learning的探索较为激进，Sarsa的探索较为保守。两者的action策略都是e-greedy，那么差异就出在的Qtable（Sarsatable）的更新策略上。

 

在靠近陷阱的区域9，一旦在某次action中尝试走入陷阱区域，两种策略均会在表中将陷阱处的state对应的数值降低，从而避免再次走入陷阱，比如Q（9，‘→’） = -100

但是Sarsa还会因此将前一步5的分值也降低，关注Q（5，‘↓’）的更新：

sarsa算法：s = 5，a = ‘↓’ ，r = -1， s' = 9，a' = ‘→’

对于q（5，‘↓’）：q_target = r + self.gamma * self.q_table.loc[s', a']
q_predict = self.q_table.loc[s, a]
q(s,a) = q(s,a) + a (q_target - q_predict)

尤其是看q_target，代表我认为动作的价值

即Sarsa还通过调整Sarsa-table的方法，劝阻机器人进入s'状态9靠近陷阱。

Q-learning算法：

q_target = r + self.gamma * self.q_table.loc[s', :].max()

对于进入s'状态9的行动，Q-learning不会因为曾经槽糕的下一步决策而降分，仅考虑下一步中最好的决策，也就会更加勇敢得靠近陷阱。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！