多元统计:聚类分析
多元统计:聚类分析
- 一. 相似性的度量
- 1.样品相似性的度量
- 2.变量相似性的度量
- 二. 系统聚类分析方法
- 1.系统聚类的思想
- 2.系统聚类的方法选择
- 3.系统聚类习题
- 三. K均值聚类分析
- 1.K均值聚类的思想
- 2.K均值聚类的方法
- 3.K均值聚类习题
- 四. 有序样品的聚类分析
- 1.有序样品的聚类的思想
- 五.系统聚类与K均值聚类SPSS实现
- 1.系统聚类与K均值聚类的区别
- 2.问题提出
- 2.1系统聚类
- 2.2K均值聚类
- 六.聚类分析与判别分析的差别
一. 相似性的度量
1.样品相似性的度量
对样品进行聚类分析时,用距离来测定样品之间的相似程度。因为我们把n个样本看作p维空间的n个点。点之间的距离即可代表样品间的相似度。常用的距离为:
(一)闵可夫斯基距离:
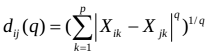
q取不同值,分为:
(1)绝对距离(q=1)
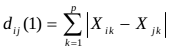
(2)欧氏距离(q=2)
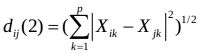
(3)切比雪夫距离(q=无穷)
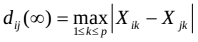
(二)马氏距离
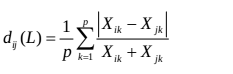
(三)兰氏距离
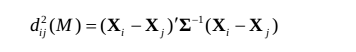
2.变量相似性的度量
对变量的相似性,我们更多地要了解变量的变化趋势或变化方向,因此用相关性进行衡量。
将变量看作p维空间的向量,一般用
(一)夹角余弦
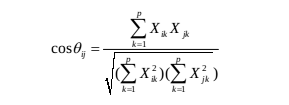
(二)相关系数
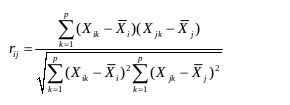
二. 系统聚类分析方法
1.系统聚类的思想
系统聚类的基本思想是:距离相近的样品(或变量)先聚成类,距离相远的后聚成类,过程一直进行下去,每个样品(或变量)总能聚到合适的类中。
2.系统聚类的方法选择
设dij表示样品Xi与Xj之间距离,用Dij表示类Gi与Gj之间的距离。
(1)最短距离法
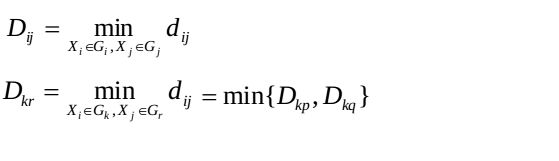
(2)最长距离法
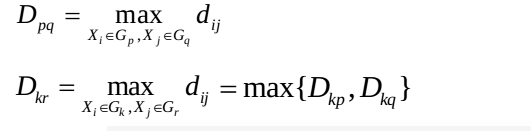
(3)中间距离法
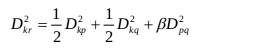
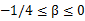
(4)重心法
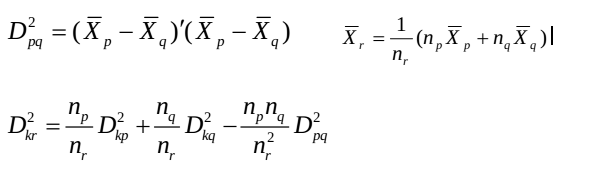
(5)类平均法
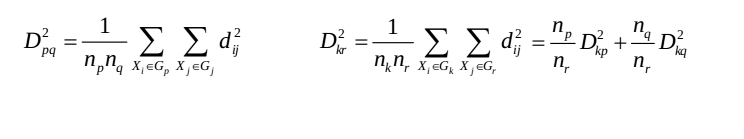
(6)可变类平均法
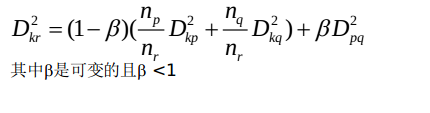
(7)可变法
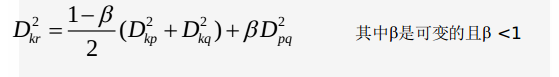
(8)离差平方和法
 通常选择距离公式应注意遵循以下的基本原则:
通常选择距离公式应注意遵循以下的基本原则:
(1)要考虑所选择的距离公式在实际应用中有明确的意义。如欧氏距离就有非常明确的空间距离概念。马氏距离有消除量纲影响的作用。
(2)要综合考虑对样本观测数据的预处理和将要采用的聚类分析方法。如在进行聚类分析之前已经对变量作了标准化处理,则通常就可采用欧氏距离。
(3)要考虑研究对象的特点和计算量的大小。样品间距离公式的选择是一个比较复杂且带有一定主观性的问题,我们应根据研究对象的特点不同做出具体分折。实际中,聚类分析前不妨试探性地多选择几个距离公式分别进行聚类,然后对聚类分析的结果进行对比分析,以确定最合适的距离测度方法。
3.系统聚类习题
最短距离与最长距离法:



三. K均值聚类分析
1.K均值聚类的思想
在数据集中根据一定策略选择K个点作为每个簇的初始中心,然后观察剩余的数据,将数据划分到距离这K个点最近的簇中,也就是说将数据划分成K个簇完成一次划分,但形成的新簇并不一定是最好的划分,因此生成的新簇中,重新计算每个簇的中心点,然后在重新进行划分,直到每次划分的结果保持不变。在实际应用中往往经过很多次迭代仍然达不到每次划分结果保持不变,甚至因为数据的关系,根本就达不到这个终止条件,实际应用中往往采用变通的方法设置一个最大迭代次数,当达到最大迭代次数时,终止计算。
2.K均值聚类的方法
3.K均值聚类习题


四. 有序样品的聚类分析
1.有序样品的聚类的思想

五.系统聚类与K均值聚类SPSS实现
1.系统聚类与K均值聚类的区别
相同:K—均值法和系统聚类法一样,都是以距离的远近亲疏为标准进行聚类的。
不同:系统聚类对不同的类数产生一系列的聚类结果,而K—均值法只能产生指定类数的聚类结果。
具体类数的确定,离不开实践经验的积累;有时也可以借助系统聚类法以一部分样品为对象进行聚类,其结果作为K—均值法确定类数的参考。
2.问题提出
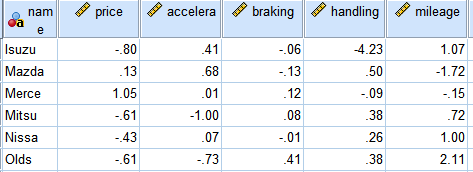
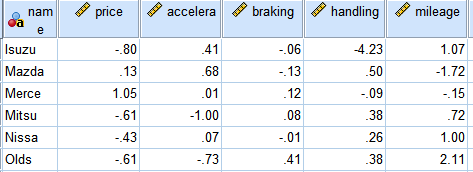
每个特定汽车是从各个制造商分别提供的汽车型号中随机选取的,现在想研究各个独立的汽车是否可以归成更有意义的类别。每辆汽车包括以下几项指标:
1、汽车的近似市场价格(price);2、汽车的加速度(accelerate);
3、汽车的刹车能力(braking);4、车辆行驶性能指数(handling);
5、汽车耗油量(mileage)。
数据中的测量单位不一样,因此在聚类之前需要对数据进行标准化,附表中数据就是已经标准化后的数据。我们的目的是要研究各个独立的汽车是否可以归类成更有意义的类别。请对以上数据利用系统聚类法及K-均值聚类法进行分类,并对样品分为四类的情况进行解释和说明。
2.1系统聚类
1.导入数据,将标准化后的5个指标导入spss中。
2.点击分析->聚类->系统聚类。并将数据放置如下图所示。

3.点击图->谱系图,并输出

4.系统聚类结果,结果如图所示:

如果我们想大致将其分为4类,则分类结果如下所示。

2.2K均值聚类
1.导入数据,将标准化后的5个指标导入spss中。
2点击分析->聚类->K均值聚类。并将数据放置如下图所示。并将聚类数设置为4.

3.输出方差表与每类所包含的样品数表。


4.K均值聚类结果如下所示

除最后一个大于0.05外,其他分类后各变量在不同类别之间的差异显著,也说明5个变量对分类的贡献也较显著。
每类所包含的样品数:

由结果可知,K均值分类的结果与系统聚类结果一致。
六.聚类分析与判别分析的差别
判别分析即根据一定的判别准则,判定一个样本归属于哪一类。具体而言,设有n个样本,对每个样本测得p项指标(变量)的数据,已知每个样本属于k个类别(或总体)中的某一类,通过找出一个最优的划分,使得不同类别的样本尽可能地区别开,并判别该样本属于哪个总体。
聚类分析是分析如何对样品(或变量)进行量化分类的问题。在聚类之前,我们并不知道总体,而是通过一次次的聚类,使相近的样品(或变量)聚合形成总体。通俗来讲,判别分析是在已知有多少类及是什么类的情况下进行分类,而聚类分析是在不知道类的情况下进行分类。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!