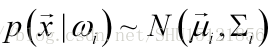模式识别实验：最小错误率贝叶斯决策（单元多元都有涉及）

目录

• • Part One 理论
  • • 一、贝叶斯理论简介
    • 二、最小错误率贝叶斯决策
    • **三、最小风险贝叶斯决策**
  • **Part Two 实操**
  • • 使用真实数据实战！
    • • 单特征
      • 2个特征
      • 3特征

整个文章大纲

• 贝叶斯理论简介
  • 先验概率
  • 后验概率
• 最小错误率贝叶斯决策
• 最小风险贝叶斯决策

Part One 理论

一、贝叶斯理论简介

如果你是理工科出身，对贝叶斯公式肯定不会陌生。
贝叶斯经常用于文档分类上，在电子邮件的过滤等文本处理上效果相当不错，最近题主在学校做的一个参加挑战杯的项目，是基于LDA贝叶斯模型，可能有些同学会有点迷糊，这里的LDA不是Linear Discriminant Analysis线性分类器，是隐含狄利克雷分布(Latent Dirichlet Allocation)

上贝叶斯公式：
p ( A ∣ B ) = p ( B ∣ A ) ⋅ p ( A ) p ( B ) p(A|B) =\frac{p(B|A)\cdot p(A)}{ p(B)} p(A∣B)=p(B)p(B∣A)⋅p(A)​

话不多说，我们来首先来看一下贝叶斯是基于什么样的思想：

新信息出现之后A的概率 = A的概率×新信息带来的调整

我在知乎上找到的维恩图很好地表现了贝叶斯公式的背后思想


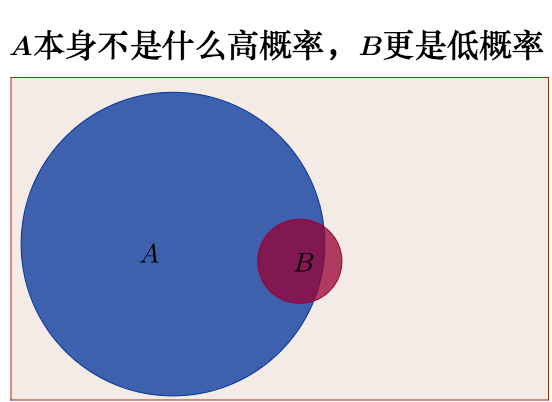
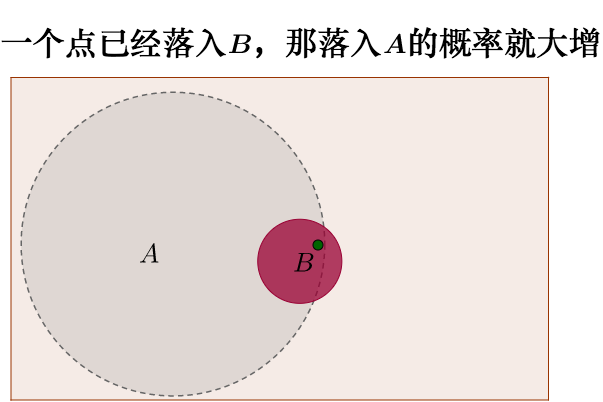
来自非数学语言解释贝叶斯定理

那么现在对于最基础的公式有了最直观的理解之后，那我们就可以学习怎么把这个思想运用到分类上。
我们用先验概率和类条件概率的乘积，代替后验概率去做比较：

其实很简单，我来举个例子
现在有2类硬币：
* 1元
* 0.5元
目前知道的有这两类硬币数量的比例，这是一个先验概率噢，比如说，为了简便，我取1:1，每一种类别的频率都为0.5
那么现在我们想要根据测量硬币的重量来进一步预测这个硬币到底是1元的还是5角的
我们就可以根据贝叶斯公式推算出未知硬币的分别属于哪种硬币的概率，取概率大的为预测结果。
那你现在可能就会有问题了，后验概率怎么来的呢？
好问题，这也是贝叶斯的一个小bug，后验概率一般是根据数据得出，你可以看出其实这里不能做到完全严谨。

在一般应用中我们假设这个特征在类内是服从正态分布的(实际上生活中很多特征都是这样的)，正态分布由两个参数唯一决定，均值和方差。所以完全可以用训练集中的特征的出现情况去估计这两个参数，从而得到类条件概率密度函数的模型。

• 高斯分布：
  
  接下来我们来学习什么是最小错误率贝叶斯决策

二、最小错误率贝叶斯决策

如下图，如果类条件概率密度函数和先验概率的乘积图像是这样的，那么在交点处作为分类面，对于特征的值x取在分类面左边的样本预测为红色类别，右边的样本预测为绿色类别，总的错误率最小：
图中一半阴影即是把绿色类误判为红色类的情况，一半阴影是把红色类误判为绿色类的情况。只有分类面取在交点处时这个错误率之和才能最小。
如果不是取在交点处，不管是在左边还是右边，可以看到错误的面积总是会比刚刚那种情况多出一块：

如此我们可以得到：
以二分类问题为例，对于样本x的决策错误率：

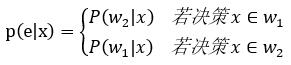
更进一步得到:

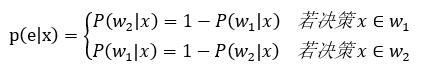
决策函数：

讨论多分类问题：
如果认为样本的特征向量在类内服从多元正态分布：

类条件概率密度服从多元正态分布，带入，得：

• 多元正态分布
  p ( x ) = 1 ( 2 π ) 1 / 2 ∣ ∑ ∣ 1 / 2 exp ⁡ { − 1 2 ( x − μ ) T ∑ − 1 ( x − μ ) } , x ∈ R l p(x)=\frac{1}{(2\pi)^{1/2}|\sum|^{1/2}}\exp {\{-\frac{1}{2}(x-\mu)^T{\sum}^{-1}(x-\mu)\}}, \quad x \in R^l p(x)=(2π)1/2∣∑∣1/21​exp{−21​(x−μ)T∑−1(x−μ)},x∈Rl
• mean均值
  μ = E [ x ] = E [ x 1 , x 2 , . . . . . , x l ] \mu = E[x] = E[x_1,x_2,.....,x_l] μ=E[x]=E[x1​,x2​,.....,xl​]
• 协方差矩阵：
  ∑ = E [ ( x − μ ) ( x − μ ) T ] = [ σ 11 2 σ 12 2 ⋯ σ 1 l 2 σ 21 2 σ 22 2 ⋯ σ 2 l 2 ⋮ ⋮ ⋱ ⋮ σ l 1 2 σ l 2 2 ⋯ σ l l 2 ] \sum = E[(x-\mu)(x-\mu)^T]\\ = \begin{bmatrix} \sigma_{11}^2 & \sigma_{12}^2 & \cdots & \sigma_{1l}^2\\ \sigma_{21}^2 & \sigma_{22}^2 & \cdots & \sigma_{2l}^2\\ \vdots & \vdots & \ddots & \vdots\\ \sigma_{l1}^2 & \sigma_{l2}^2 & \cdots & \sigma_{ll}^2\\ \end{bmatrix} ∑=E[(x−μ)(x−μ)T]=⎣⎢⎢⎢⎡​σ112​σ212​⋮σl12​​σ122​σ222​⋮σl22​​⋯⋯⋱⋯​σ1l2​σ2l2​⋮σll2​​⎦⎥⎥⎥⎤​
• 决策函数
  (0) g i j ( x ) = g i ( x ) − g j ( x ) = 0 g_{ij}(x) = g_i(x) - g_j(x) = 0 \tag 0 gij​(x)=gi​(x)−gj​(x)=0(0)
  由于x符合正太分布，带入可得最终决策函数
  =>
  g i ( x ) = − 1 2 l n ( 2 π ) − 1 2 l n ∣ Σ i ∣ − 1 2 ( x − μ i ) T Σ i − 1 ( x − μ i ) + l n p ( w i ) g_i(x) = -\frac{1}{2}ln \ (2\pi) - \frac{1}{2}ln \ |\Sigma_i| - \frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i) + ln \ p(w_i) gi​(x)=−21​ln (2π)−21​ln ∣Σi​∣−21​(x−μi​)TΣi−1​(x−μi​)+ln p(wi​)
  这里题主采用了rev_gi，取了相反数，在比较大小的时候取最小值的决策函数就是我们的最终结果的取值
  (1) r e v ( g i ) = − g i ( x ) = 1 2 l n ( 2 π ) + 1 2 l n ∣ Σ i ∣ + 1 2 ( x − μ i ) T Σ i − 1 ( x − μ i ) − l n p ( w i ) rev(g_i) = -g_i(x) = \frac{1}{2}ln \ (2\pi) + \frac{1}{2}ln \ |\Sigma_i| + \frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i) - ln \ p(w_i) \tag 1 rev(gi​)=−gi​(x)=21​ln (2π)+21​ln ∣Σi​∣+21​(x−μi​)TΣi−1​(x−μi​)−ln p(wi​)(1)
  而根据决策面有
  g i j ( x ) = g i ( x ) − g j ( x ) = 0 g_{ij}(x) = g_i(x) - g_j(x) = 0 gij​(x)=gi​(x)−gj​(x)=0
  可以得到我们的决策面：
  (2) − 1 2 [ ( x − μ i ) T Σ i − 1 ( x − μ i ) − ( x − μ j ) T Σ j − 1 ( x − μ j ) ] − 1 2 l n ∣ Σ i ∣ Σ j + l n p ( w i ) p ( w j ) = 0 -\frac{1}{2}[(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i) - (x-\mu_j)^T\Sigma_j^{-1}(x-\mu_j)] - \frac{1}{2}ln \ \frac{|\Sigma_i|}{\Sigma_j} + ln \ \frac{p(w_i)}{p(w_j)} = 0 \tag 2 −21​[(x−μi​)TΣi−1​(x−μi​)−(x−μj​)TΣj−1​(x−μj​)]−21​ln Σj​∣Σi​∣​+ln p(wj​)p(wi​)​=0(2)

三、最小风险贝叶斯决策

码累了，下次补充

Part Two 实操

封装的算法是仿sklearn的风格。这里我用的accuracy_score直接调用sklearn的了，在后续的博客中（可能很慢，但是寒假来临后，会更新比较快，都是手码字，有些慢）
这段代码逻辑其实很清晰(某人自认为，不接受反驳！X^X)

• 在init中一些必要的变量给加进去了，均值和协方差很重要！
• Bayes中按情况传入先验概率，没传就计算出样本中各类的概率作为先验概率
• 这里的decision_fuction其实是为了画出模型的ROC曲线，而依据的公式是(0)公式，决策面以右方的0来决定，而现在画ROC取的阙值可以取这右边的值，也就是说，我们可以取两者之差不为0的值作为新的决策阙值，来看模型在哪一个取值上会有更好的效果
• 在计算决策函数的时候，由于numpy的inv传入的值为1维（0维），会疯狂报错，所以这里需要对1个特征的进行特殊处理

import numpy as np
from numpy.linalg import inv
from sklearn.metrics import accuracy_scoreclass BayesGN:def __init__(self, priors=None):"""初始化Linear Regression模型"""self.priors = priorsself._mean = Noneself._cov = Nonedef fit(self, X_train, y_train):"""sorted_y 和priors对应的类别序号相对应"""X_train = np.array(X_train)y_train = np.array(y_train)sorted_y = np.sort(np.unique(y_train))if self.priors is None:c = Counter(y_train)_sum = sum(c.values())self.priors = [c[y] / _sum for y in sorted_y]self._mean = [X_train[y_train == y].mean(axis=0) for y in sorted_y]self._cov = [np.cov(X_train[y_train == y].T) for y in sorted_y]return selfdef predict(self, X_predict):"""给定带预测数据集X_predict,返回表示X_predict的结果向量"""y_predict = [self._predict(x) for x in X_predict]return np.array(y_predict)def _predict(self, Xi):return np.argsort(self._rvs_g(Xi))[0]def decision_function(self, X_test):b = [self._rvs_g(X_test[i])[0]-self._rvs_g(X_test[i])[1] for i in range(len(X_test))]return bdef score(self, X_test, y_test):"""根据数据集X_test，y_test计算准确度 分类准确度使用accuracy_score"""y_predict = self.predict(X_test)return accuracy_score(y_test, y_predict)def _rvs_g(self, Xi):if self._cov[0].ndim == 0:rvs_g = [(Xi - self._mean[i]) / self._cov[i] + np.log(self._cov[i]) - 2 * np.log(self.priors[i]) for i inrange(len(self._mean))]else:rvs_g = [np.matmul(np.matmul((Xi - self._mean[i]), inv(self._cov[i])),(Xi - self._mean[i])) +np.log(np.linalg.det(self._cov[i])) - 2 * np.log(self.priors[i]) for i in range(len(self._mean))]return rvs_g

使用真实数据实战！

• 这里使用的数据来自参加上海大学模式识别中的历年男女学生的真实数据
• 详情可见题主的Soledadzyh’s github

单特征

2个特征

• 此处开始涉及parzen窗，题主下次再添加上相关资料

3特征

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！