个人笔记:开发中常用的数学计算式
个人开发时经常用到一些公式,以往都是临时保存一个书签,查找比较麻烦,特此做一个记录,转载保留了地址。工作之余不定时更新。(伪代码。很多类型未申明)
三点求平面方程、平面法向量和点到平面的距离
三点p1(x1,y1,z1),p2(x2,y2,z2),p3(x3,y3,z3),
//已知3点坐标,求平面ax+by+cz+d=0;void get_panel(Point p1,Point p2,Point p3,double &a,double &b,double &c,double &d){a = (p2.y - p1.y)*(p3.z - p1.z) - (p2.z - p1.z)*(p3.y - p1.y);b = (p2.z - p1.z)*(p3.x - p1.x) - (p2.x - p1.x)*(p3.z - p1.z);c = (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x);d = 0 - (a * p1.x + b*p1.y + c*p1.z);}// 已知三点坐标,求法向量Vec3 get_Normal(Point p1,Point p2,Point p3){a = (p2.y - p1.y)*(p3.z - p1.z) - (p2.z - p1.z)*(p3.y - p1.y);b = (p2.z - p1.z)*(p3.x - p1.x) - (p2.x - p1.x)*(p3.z - p1.z);c = (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x);return Vec3(a, b, c);}//点到平面距离double dis_pt2panel(Point pt,double a,double b,double c,double d)
{return f_abs(a * pt.x + b*pt.y + c*pt.z + d) / sqrt(a * a + b * b + c * c);}————————————————
版权声明:本文为CSDN博主「Bigdz」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/newproblems/article/details/77651517两点求直线方程
ax+by+c=0
double a = p2.getY() - p1.getY();
double b = p1getX() - p2.getX();
double c = p2.getX() * p1.getY() - p1.getX() * p2.getY();弧度
由角度算弧度:弧度数=角度数÷180°×π;
由弧度算角度:角度数=弧度数÷π×180°。
式中角度数用单位“°”且要写上,弧度数不用单位。
C++ 使用弧度计算
坐标是否在角度范围内:
UGbool IsPointInAngle(UGPoint2D p, UGdouble angleStart, UGdouble angleEnd){
//计算弧度double pi = 3.1415926535;UGdouble radianStart = angleStart / 180 * pi;UGdouble radianEnd = angleEnd / 180 * pi;
//让弧度为正值if (radianEnd < 0){radianEnd += 2 * pi;}if (radianStart < 0){radianStart += 2 * pi;}
//考虑特殊情况,比如 起始为-30(330度),终点60(420度)。目标角度在30(390)。
//目标角度有两种表示。任意一种落在范围内即可。if (radianStart>radianEnd){radianEnd += 2 * pi;}UGdouble radianP = 0;UGdouble radianP2 = 0;UGdouble dis = sqrt(p.x*p.x + p.y*p.y);//根据acos计算弧度,因为acos只处理0-180度,因此分两个情况if (p.y > 0)//0-180{radianP = acos(p.x / dis);radianP2 = radianP + pi;}else//180-360{radianP = 2 * 3.1415926 - acos(p.x / dis);radianP2 = radianP + pi;}if ((radianStart < radianP&&radianP < radianEnd)|| (radianStart < radianP2&&radianP2 < radianEnd)){return true;}return false;}求解一元四次方程:
#include
#include
#include
#include
/******************************************************************************\
对一个复数 x 开 n 次方
\******************************************************************************/
std::complex sqrtn(const std::complex&x,double n)
{double r = hypot(x.real(),x.imag()); //模if(r > 0.0){double a = atan2(x.imag(),x.real()); //辐角n = 1.0 / n;r = pow(r,n);a *= n;return std::complex(r * cos(a),r * sin(a));}return std::complex();
}
/******************************************************************************\
使用费拉里法求解一元四次方程 a*x^4 + b*x^3 + c*x^2 + d*x + e = 0
\******************************************************************************/
std::complex Ferrari(std::complex x[4]
,std::complex a
,std::complex b
,std::complex c
,std::complex d
,std::complex e)
{a = 1.0 / a;b *= a;c *= a;d *= a;e *= a;std::complex P = (c * c + 12.0 * e - 3.0 * b * d) / 9.0;std::complex Q = (27.0 * d * d + 2.0 * c * c * c + 27.0 * b * b * e - 72.0 * c * e - 9.0 * b * c * d) / 54.0;std::complex D = sqrtn(Q * Q - P * P * P,2.0);std::complex u = Q + D;std::complex v = Q - D;if(v.real() * v.real() + v.imag() * v.imag() > u.real() * u.real() + u.imag() * u.imag()){u = sqrtn(v,3.0);}else{u = sqrtn(u,3.0);}std::complex y;if(u.real() * u.real() + u.imag() * u.imag() > 0.0){v = P / u;std::complex o1(-0.5,+0.86602540378443864676372317075294);std::complex o2(-0.5,-0.86602540378443864676372317075294);std::complex&yMax = x[0];double m2 = 0.0;double m2Max = 0.0;int iMax = -1;for(int i = 0;i < 3;++i){y = u + v + c / 3.0;u *= o1;v *= o2;a = b * b + 4.0 * (y - c);m2 = a.real() * a.real() + a.imag() * a.imag();if(0 == i || m2Max < m2){m2Max = m2;yMax = y;iMax = i;}}y = yMax;}else{//一元三次方程,三重根y = c / 3.0;}std::complex m = sqrtn(b * b + 4.0 * (y - c),2.0);if(m.real() * m.real() + m.imag() * m.imag() >= DBL_MIN){std::complex n = (b * y - 2.0 * d) / m;a = sqrtn((b + m) * (b + m) - 8.0 * (y + n),2.0);x[0] = (-(b + m) + a) / 4.0;x[1] = (-(b + m) - a) / 4.0;a = sqrtn((b - m) * (b - m) - 8.0 * (y - n),2.0);x[2] = (-(b - m) + a) / 4.0;x[3] = (-(b - m) - a) / 4.0;}else{a = sqrtn(b * b - 8.0 * y,2.0);x[0] =x[1] = (-b + a) / 4.0;x[2] =x[3] = (-b - a) / 4.0;}
return x[4];
}int main()
{
std::complex x[4];
x[4] = Ferrari(x,1,2,3,4,5); //验证费拉里法
std::cout<<"root1: "< 旋转计算,
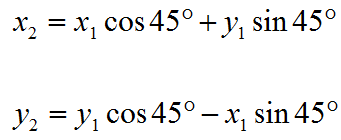
顺时针:
x2 = xcos + ysin;
y2 = ycos - xsin;
逆时针:
x2 = xcos - ysin;
y2 = ycos + xsin;
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!