多项式乘法,FFT与NTT
多项式:
多项式?不会
多项式加法:
同类项系数相加;
多项式乘法:
A*B=C
$A=a_0x^0+a_1x^1+a_2x^2+...+a_ix^i+...+a_{n-1}x^{n-1}$
$B=b_0x^0+b_1x^1+b_2x^2+...b_ix^i+...+b_{m-1}x^{m-1}$
则
$C=c_0x^0+c_1x^1+c_2x^2+...c_ix^i+...+c_{m+n-2}x^{m+n-2}$
其中
$$c_k=\sum_{i+j=k}^{i 我们又称其为多项式的卷积运算。 使用定义法,直接进行卷积运算的期望效率为$O(n^2)$ 一个n次多项式(这里定义为最高项指数为n-1)可以被其图像上n个不重复的点表示(当然大于n个点也可) 于是这N个有序数对被称为一个多项式的点值表达式 多项式上任意N个不重复的有序数对皆可 随便找N个X坐标,依次求其Y坐标,使用(数学必修2称秦九韶算法|算导称霍纳法则)可得到单次$O(n)$整体$O(n^2)$的效率 这一过程被称作DFT; 一种通过多项式的点值表达式求其系数的方法; 常用的是拉格朗日插值法; 设多项式A的点值表达式为点集 {$(x_0,y_0),(x_1,y_1),...,(x_{n-1},y_{n-1})$} 则: $$A(x)=\sum_{k=0}^{x-1}y_k{{\Pi_{j!=k}(x-x_j)}\over{\Pi_{j!=k}(x_k-x_j)}}$$ 拉格朗日插值法的构造无疑是正确的,然而观察上式即可发现其效率也是$O(n^2)$的; (不用仔细研究上面的式子,今天她不重要) 差值是DFT的逆变换 FFT与NTT是在$O(nlog_2n)$的时间内解决多项式卷积的算法; (NTT可以用于模意义下的多项式卷积——模某些大费马数) 直接运用定义在已知系数的前提下进行卷积,其效率是$O(n^2)$的 然而在点值表达式下,求得卷积多项式的点值表达式的效率是$O(n)$的 那么如何在$O(nlog_2n)$的时间那进行求值和差值呢 下面介绍FFT是如何求值的; 由于多项式的点值表达不限制找到的是哪些点 于是FFT是通过找到一组相互之间有联系的X坐标来优化求值过程的; fft找的X坐标是一堆复数,所以先讲复数; 定义-1的二次方根为i; i无法通过任何线性变换(扩大缩小实数倍)变为实数; 然而$i^2$=-1; 于是形如a+b*i的数称为复数; 复平面 由于i的实数倍不可能是实数; 那么如何把复数a+b*i与图形结合呢?(用图形表示复数) 虚拟一种数学工具 建立平面直角坐标系,显然该坐标系两轴中的一个可与实数(a)一一对应 那么另一个与b*i对应即可 是为复平面: 当然,比较横向和纵向的距离大小毫无意义 复平面上点与复数一一对应; 如1+i与点(1,i)对应 复数的运算 从代数上看,复数的加法相当于合并同类项,复数的乘法则是逐项相乘,注意i*i=-1 从图形上看,复数的加法相当于向量首尾相连,复数的乘法则是两项量模长相乘,与x轴的夹角相加 (计算一个(cos(u)+sin(u)i)*(cos(v)+sin(v)i)看看复数运算的代数意义与几何意义的关系,注意i*i=-1) 复单位圆 考虑枚举弧度X,则所有cos(x)+sin(x)*i的点构成复单位圆 如果强行认为i的长度等于1的长度,则复单位圆的确仿佛是一个圆 于是有了一个欧拉公式 $$e^{u*i}=cos(u)+sin(u)i$$ 函数:$f(u)=e^{u*i}$的图像可以看作是三维的,一个轴是枚举u,剩下的是复平面,她在复平面上的投影即是复单位圆。 挂个链接,感受一下。 证明: 上帝公式怎么需要证明呢(不会,孩子,自己去导吧) 设$w_n^k=cos({2k\pi\over n})+sin({2k\pi\over n})i$ 其中n,k,一般取为正整数 我们称之为n次单位复根 如下图: 几个引理: DFT 当我们求n次多项式乘m次多项式的结果时,要得到一个n+m-1次多项式; 于是需要求原来两个多项式中的n+m-1个点,再使之对应相乘; 事实上,如果在一个n次多项式上写出大于n次的项,但使其系数为0的话,一来她与原式等价,二来她的次数可以变成任意大于n次的值 我们期望在O(nlog2n)时间内求所有点值 可以猜测我们使用分治算法; 于是我们干脆把输入多项式与结果多项式都扩展为一个2s次多项式,使其次数大于n+m-1且最小(最小只是为了常数小) 那么我们求哪些x对应的y值呢 我们求所有x∈A:{$x=w_n^k$|k∈Z,0≤k 可以看出A中正好有$2^s$个元素,当然她们是互不相同的 为什么用这些东西呢? 我们求解多项式: $$A=a_0x^0+a_1x^1+a_2x^2+...+a_ix^i+...+a_{n-1}x^{n-1}$$ 在$x=x_s$时的取值,即: $$A(x_s)=a_0x_s^0+a_1x_s^1+a_2x_s^2+...+a_ix_s^i+...+a_{n-1}x_s^{n-1}$$ 设: $$A_0=a_0x^0+a_2x^1+a_4x^2+...+a_{2i}x^i+...+a_{n-2}x^{{n \over 2}-1}$$ $$A_1=a_1x^0+a_3x^1+a_5x^2+...+a_{2i+1}x^i+...+a_{n-1}x^{{n \over 2}-1}$$ 则: $$A(x_s)=A_0(x_s^2)+x_sA_1(x_s^2)$$ 若把$x_s$分别带为$w_n^s$ 则由于折半引理 $$A(w_n^{s+{n \over 2}})=A_0((w_n^s)^2)-w_n^sA_1((w_n^s)^2)$$ 于是$A_0$,$A_1$分别只有n/2项,要求解的w也只有n/2个; 运用消去引理 $$(w_n^s)^2=w_{n \over 2}^s$$ $$A(w_n^s)=A_0((w_n^s)^2)+x_sA_1((w_n^s)^2)=A_0(w_{n \over 2}^s)+w_n^sA_1(w_{n \over 2}^s)$$ 于是对于$A_0$与$A_1$的求解情况变得与A类似了(只是由n变为n/2——问题规模减半) 再递归下去即可; 递归版代码: 有非递归版谁写递归版啊! 找一个项数为8的多项式,逐层模拟其递归分治过程,观察其多项式的系数; 发现其最后一层的序列中排第i的多项式的唯一的系数的下标是i的二进制串,不到8的01串这么长就补0,然后翻过来得到的数; 有了这个规律直接求出最后一层的结果,然后逐层上推即可; (显然最后一层的系数是常数项的) 代码: IDFT 把多项式的n个系数看做n维向量,函数值看做n维向量 构造DFT矩阵V: (来自Yveh学长的课件) 构造其逆矩阵D,即是IDFT的矩阵: (来自Yveh学长的课件) 讲这么多其实就是之前FFT的代码,t=1时求对应系数下的DFT,t=-1时求对应函数值下的IDFT NTT解决的是模意义下的多项式卷积——只是模了常数,不是模了x的多少次方;(系数取模,不是多项式模) 下面介绍NTT是如何求值的; 由于多项式的点值表达不限制找到的是哪些点 于是NTT是通过找到一组相互之间有联系的X坐标来优化过程的; 群的相关 与模数互质的数集的原根的某些次方具有和单位复根相似的性质,于是NTT取原根的某些次方为x; 定义有限群(A,·)的原根g,为 既然这样:A={x|x=$g^k$,k∈$Z_+$} 可以看出,1≤k≤|A|时$g^k$各不相同(否则提前出现了循环,就会使A集合中元素个数不到|A|个) 既然,$g^k$在1≤k≤|A|中必有一个单位元,那么只能是$g^{|A|}$了; 给定一个正整数P,与其互质的小于她的数的集合,在乘法下构成一个群; 这里只讨论P为质数; 她是一个有限群,(只有P-1个元素); 于是她是有限群的一个例子; 她的原根也是有限群原根的一个例子; 于是在模P意义下, 取原根的所有次方可以有P-1个不同取值, 在多项式求值时取她们的话, 应该比我们需要的点数多不少 然而我们只需要原根的某些次方,还希望她们满足与单位复根类似的性质 ——这样只要把FFT模板中的单位复根换成原根的某些次方,且把复数运算换成模运算就好了 这里讨论在$P=C2^k+1$且$2^k$大于我们需要的点数时的解法 (一种常见的情况,P这时被称作费马数) 设需要点数为n(这里的n已经被扩展为2的某次方); 设$g_n^0=g_n^n=g^{P-1}=g^{C2^k}=1$ 这样的话$g_n^1=g^{C2^k \over n}$ $g_n^s=g^{Cs2^k \over n}$ 在s取0到n-1时互不相同; 且满足消去,折半引理;(这里的减号是模意义下的减号) 非递归代码如下: t=1时求对应系数下的DFT,t=-1时求对应函数值下的IDFT NTT中DFT与IDFT的关系与FFT中类似,只是除len改为乘其逆元,然而上面这个是优化过的代码,看起来IDFT与FFT的IDFT部分不太一样。 不再赘述; 给一个总模板: uoj #34(NTT也可解决整数系数却没模数的问题,自己取个大费马数做模数即可) 卷积与FFT的理解方法几条 FFT总结 其实都写得挺好的 然而,这个东西真的只是背模板即可啊 转载于:https://www.cnblogs.com/nietzsche-oier/p/7435539.html离散傅里叶变换(DFT):
插值(IDFT):
FFT与NTT:
FFT(快速傅里叶变换Fast Fourier Transform)
复数:
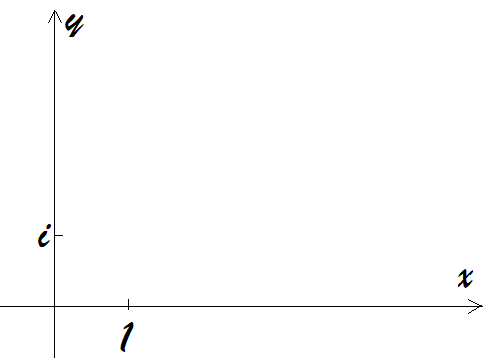
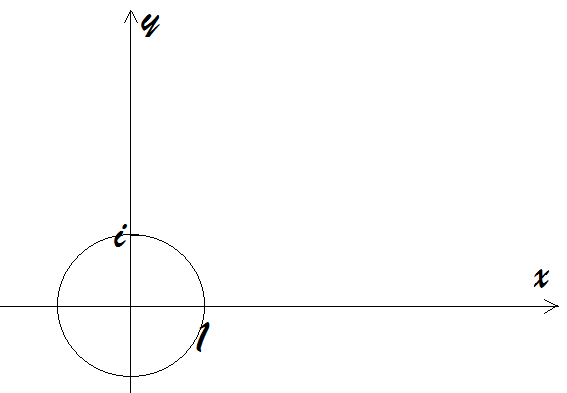
单位复根

实现DFT与IDFT
//not found;
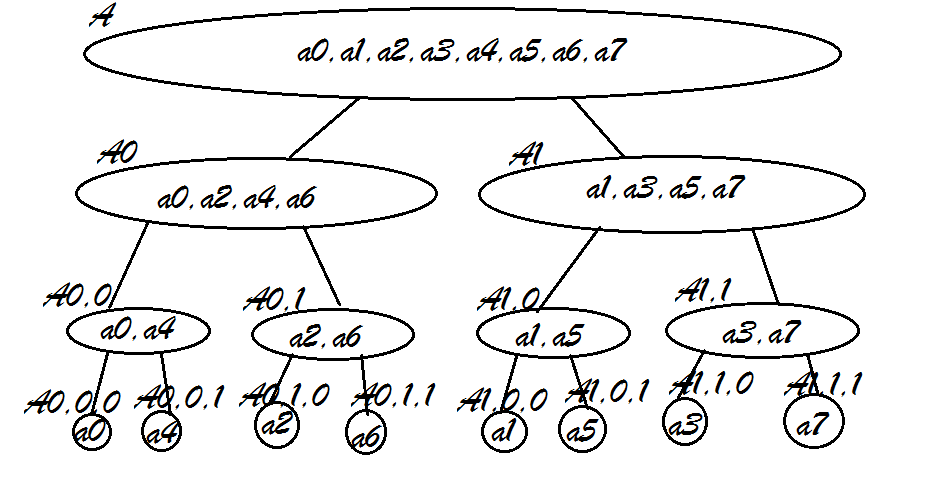
//f[]开始时盛放系数,最后盛放函数值
//t输入1时,为DFT,输入-1时,为IDFT,之后再讲
void FFT(Complex_num f[],int t){int i,j,k,lim;Complex_num f0,f1;ra(f);
//交换系数,使之变成最后一层的情况for(k=2;k<=len;k<<=1){//每个k对应一层,k是该层单个多项式的系数个数,从倒数第二层开始lim=(k>>1);w[0].generate(1,0);w[1].generate(cos(2*Pi*t/k),sin(2*Pi*t/k));for(i=2;i


NTT(快速数论变换Fast Number-Theoretic Transform)
生成子群与原根
正题
void NTT(LL f[],int t){int i,j,k,lim;LL f0,f1,inv;ra(f);for(k=2;k<=len;k<<=1){lim=k>>1;g[0]=1;g[1]=rc[k];for(i=2;i


#include
NTT 

#include
FFT 最后帮同学刷访问量:
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!
