数据结构之单链表的相交与环的问题

一、单链表相交不带环

如果两个单链表不带环，可以把它们的相交分成以下两种情况： T型、V型

T型：

这种形式的相交指的是一个单链表的尾（注意：这里只能是尾而不能是头）指向了另一个单链表的中间位置。

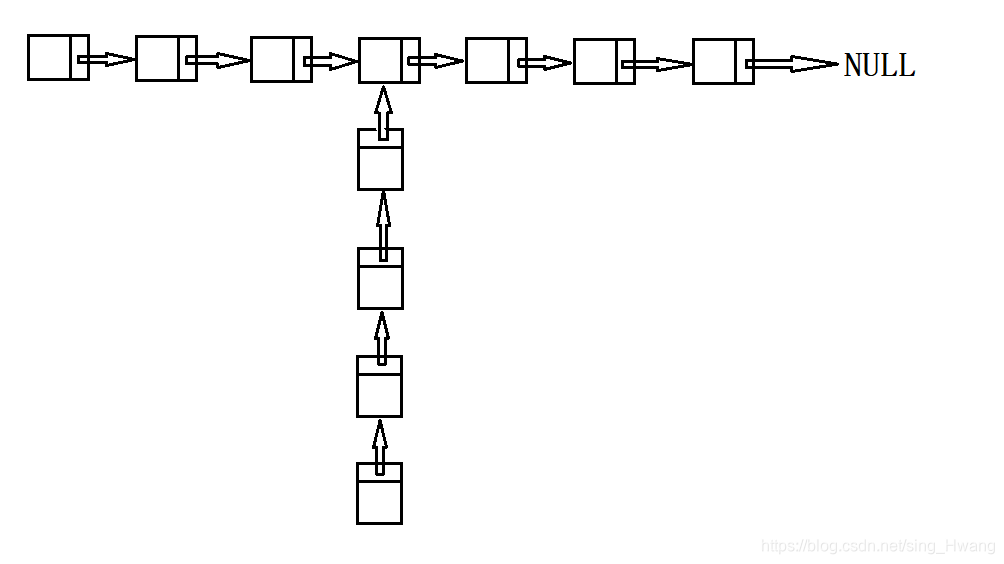
V型：

这种形式的相交，指的是一个单链表的尾指向了另一个单链表的尾。值得注意的是这里只能是被指向单链表的尾，因为如果是被指向单链表的头部，那么两个单链表实际上是一个更大的单链表而已！ 

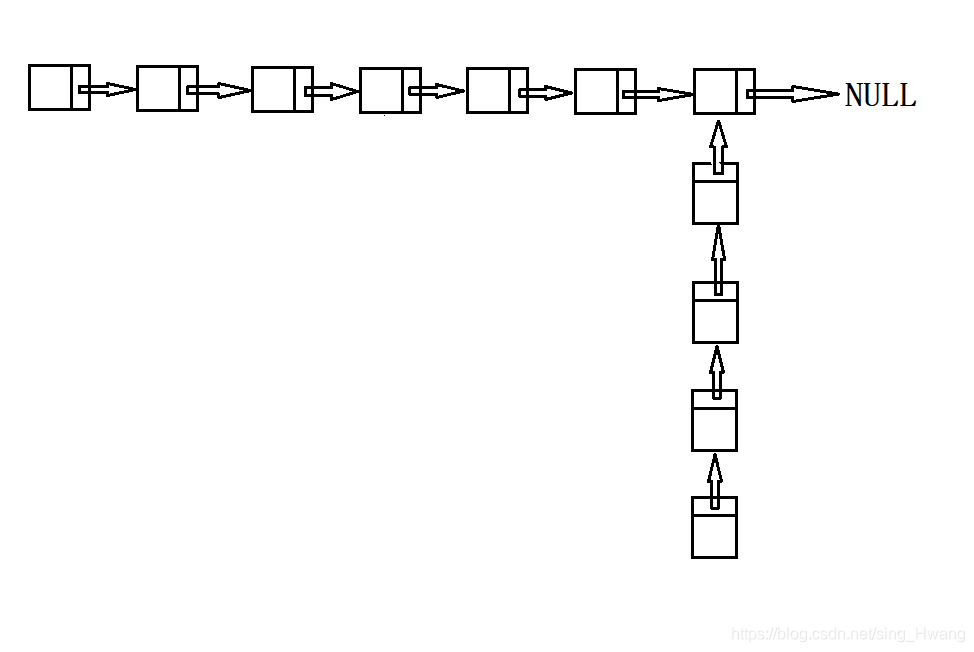
判断相交：

如果仅仅是判断两个不带环的单链表是否相交，那很简单——上述两种相交形式的结果都是一样的：若相交，则两链表的尾结点必然相同！

我们只需要分别遍历两个链表，对尾结点进行判断即可。时间复杂度为O(len1 + len2)，空间复杂符为O(1) （代码就不过于赘述）

求交点：

若是要求交点，就有点点复杂了：

如果两个单链表相交，我们可以分别求出两个链表的长度，把两个链表的长度差记为sub。那么只需让长链表的指针先走sub步，然后让两个链表的指针同步走，那么必然会走到交点处。

在代码实现方面就比较灵活了： 

可以在求出两链表长度后，让两链表指针往后移动的过程中，判断指针是否走到了NULL的位置。若是，则说明两链表根本就不相交！ 

也可以让在求两个链表的长度时，顺便比较两个链表的尾结点，判断是否相交。若不相交，就不用求交点了。

这里使用的第二种方案：

PNode GetCorssNode(PNode pHead1, PNode pHead2)
{PNode pN1 = pHead1;PNode pN2 = pHead2;int len1 = 0;int len2 = 0;    if (pHead1 == NULL || pHead2 == NULL)   //若其中一个链表为空，则错误{        return NULL}    while(pN1)  //求第一个链表的长度{len1++;pN1 = pN1->next;}    while(pN2)  //求第二个链表的长度{len2++;pN2 = pN2->next;}    if (pN1 == pN2) //如果有交点，则求交点。没有交点则返回NULL{int count = len1-len2;pN1 = pHead1;pN2 = pHead2;        if (len1>=len2) //若第一个链表长，就让第一个链表的指针先走{ while(count>0){pN1 = pN1->next;count--;}}        else            //若第二个链表长，就让第二个链表的指针先走{            while(count<0){pN2 = pN2->next;count++;}}        while(pN1 && pN2)   //两指针同步走，走到交点就返回{            if (pN1 == pN2){                return pN1;}pN1 = pN1->next;pN2 = pN2->next;} }    return NULL;
}

二、单链表带环

单链表带环有以下几种情况：6型、0型

6型：

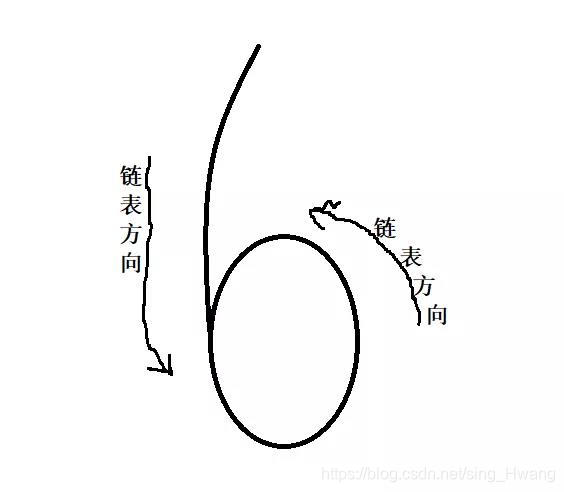
0型：

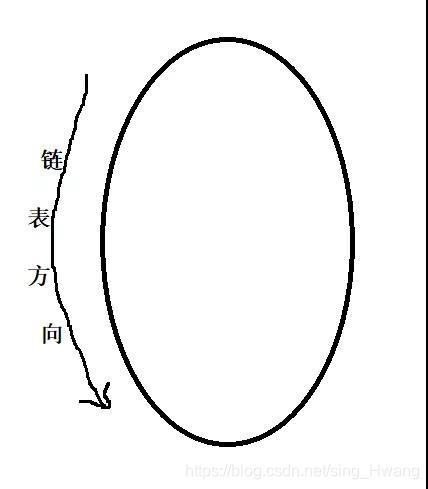
判断环：

判断环有一个小技巧：设两个指针，开始时都指向链表的头部。

让一个指针一步一步地走（一次走一步）；让另一个指针两步两步地走（一次走两步）。那么，链表若是带环，无论是不是自环，两指针必定会在环内相遇。 

有人可能会想，若是不带环呢，那两个指针岂不是一直无限循环？实则不然：若是单链表不带环，那么走得快的指针必然会走到NULL。

PNode IsListWithCircle(PNode pHead1)  // 判断单链表是否带环，返回相遇点。{PNode pFas = NULL;PNode pSlo = NULL;    if (pHead1 == NULL){        return NULL;}pFas = pHead1;pSlo = pHead1;    while(pFas && pFas->next){pSlo = pSlo->next;pFas = pFas->next->next;        if (pFas == pSlo){            return pFas;}}    return NULL;
}

求环入口点：

若是自环，任何一个结点都可视为入口点。只需要用两个指针，一个固定，一个往后走，判断出该环是自环即可。

若不是自环，即就是“6”这种情况。如图所示：

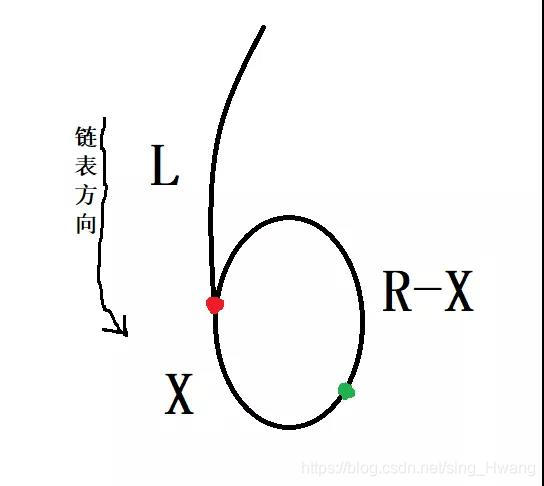
红点为入口点，绿点为在判断环时两个指针最终的交点；将从开始结点到入口结点的长度记为L，将入口点到两指针交点的长度记为X，将环的周长记为R。

在判断环相交的时候，我们是让一个指针一次走一步（把该指针记为慢指针），让另外一个指针一次走两步（把该指针记为快指针）。那么两指针相遇时，快指针走的距离一定是慢指针走的距离的2倍。

有如右关系：2*(L+x+z*R)=L+x+m*R 

将上式化简整理得：L=R-X+(n-1)*R

这里的L+X+z*R为慢指针走的距离，L+X+m*R为快指针走的距离，z和m分别为慢指针和快指针转的圈数。n等于m-2*z。

根据上式，我们便可让两个指针，一个从头开始、另一个从相遇点（绿点）开始，两指针一次都是一次走一步。

那么，当从头开始出发的指针走到环的入口点（红点）时，从相遇点开始出发的指针必然会在转过若干圈之后同样走到环的入口点。

PNode GetCircleEnter(PNode pHead1, PNode pMeetNode)    // 获取环的入口点{PNode pHea = pHead1;PNode pMee = pMeetNode;    if(pMeetNode == NULL)        return NULL;    while(1){        if (pHea == pMee){            return pHea;}pHea = pHea->next;pMee = pMee->next;}
}

三、单链表带环相交

判断是否相交：

若链表带环，看起来情况更加复杂，实际上也很简单，我们来分析一下：

单链表带环的相交情况只有一种：只有当两个单链表都带环时，它们才可能相交！ 

若是一个带环而另一个不带环，会出现什么结果？下面以图示说明：

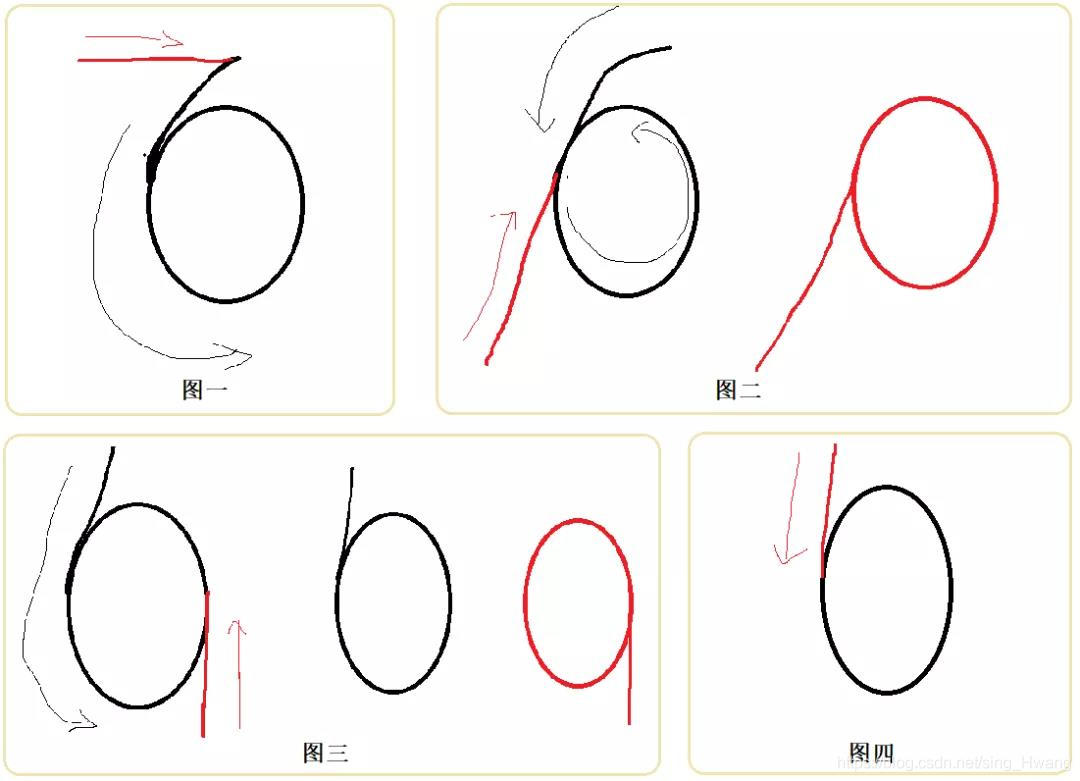
一个带环另一个不带环的相交只有以上四种情况。

图一： 一个不带环链表的尾接到了带环链表的头，看起来虽然是两个链表，但实际上是一个链表而已。 

图二： 不带环的链表接到了带环链表的环入口点。这样的话红不带环链表就相当于图二右侧的红色带环链表。也就是说，图二其实是由两个带环组成的。 

图三： 不带环的链表尾部接到了带环链表的环上。这本质还是两个带环链表。 

图四： 不带环的链表尾部接到了一个自环链表上。这还是可以看做两个带环链表。 

还有一种情况没有画出来：就是一个不带环链表的尾部接到了带环链表的头和环入口点之间——这其实还是两个带环链表而已。

所以，所有的单链表带环相交问题最终都是两个带环链表的相交问题。

我们只需判断出这两个单链表是否都带环，然后针对不同情况做出不同动作即可。这里做出归纳：

1. 两个都不带环——用单链表不带环的解决方法 
2. 只有一个带环——两链表不相交 
3. 两个链表都带环——若相交，则两个链表必定有公共的环。我们只需要记录一个带环链表的中环的一个结点，然后遍历另一个带环链表，看其是否存在与被记录结点相同的结点即可。

求两个相交的带环单链表交点：

在上面判断带环单链表是否相交时，我们分别求出了两链表的环入口点，通过对比入口点的情况来进行判断。在求交点时，同样可以利用环入口点来切入。如下图所示，列出了两个相交带环链表所有可能的四种相交方式： 

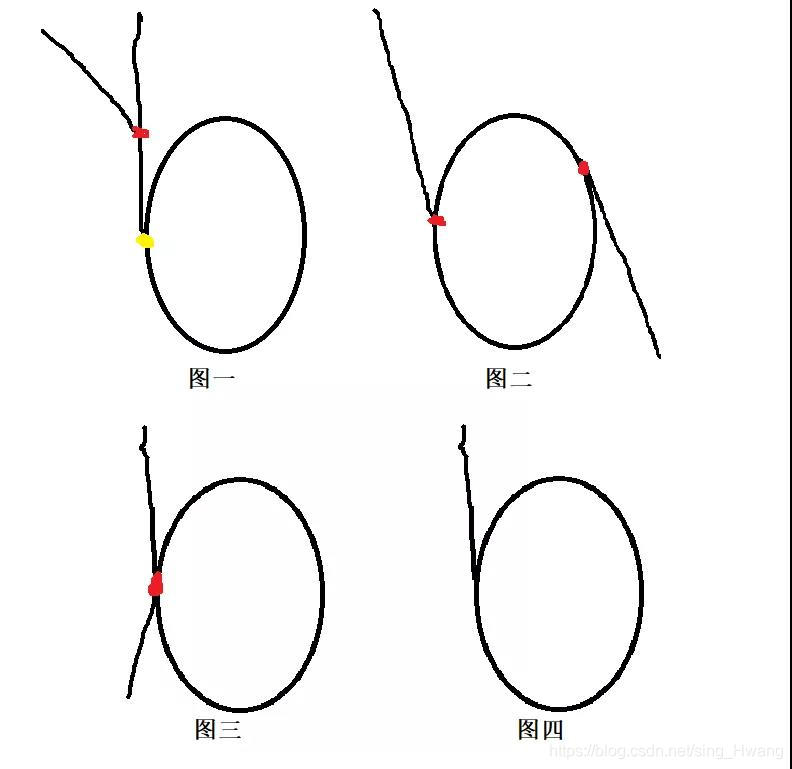
图一： 红点为两带环链表的交点，黄点为它们的环的入口点。两带环链表在到达环之前相交。 

图二： 红点为两带环链表环的入口点，认为该点同样是它们的交点。两带环链表在环上相交。 

图三： 红点为两带环链表的的交点，该点同样是两链表的环入口点。两带环单链表在环的入口点处相交。 

图四： 即判断带环链表是否相交时的图四，这里认为两个带环链表完全重合。

经分析可知，当拿到两个带环单链表的环入口点后，就可以很方便地解决以上四种情况： 

若两个环的入口点不同，则两带环单链表的交点就是环的入口点。 
若两个环的入口点相同，就从头到环入口点分别遍历两个单链表。在遍历的过程中，我们可以得到从头到环入口点这段链路的长度，利用该长度就可以求出两链表第一次相同的结点，即交点。

PNode MeetingNodeWithCircle(PNode pHead1, PNode pHead2) //求带环链表的相交点（已知相交）{PNode pC1 = GetCircleEnter(pHead1);  //得到链表1的环入口点PNode pC2 = GetCircleEnter(pHead2);  //得到链表2的环入口点PNode pH1 = pHead1;PNode pH2 = pHead2;int len1 = 1;int len2 = 1;int SubLen = 0;    if (pC1 != pC2)   //对应图二的情况{        return pC1;}    while(pH1 != pC1)   //求出第一条链表从头到环入口点的长度{len1++;pH1 = pH1->next;}    while(pH2 != pC1)   //求出第二条链表从头到环入口点的长度{len2++;pH2 = pH2->next;}pH1 = pHead1;pH2 = pHead2;    if (len1 >= len2)   //让长度较长的对应的指针先走SubLen步{SubLen = len1-len2;        while(SubLen--){pH1 = pH1->next;}}    else{SubLen = len2-len1;        while(SubLen--){pH2 = pH2->next;}}    while(pH1 != pH2)   //两指针一起走，遇到第一个相同的结点就停下来{pH1 = pH1->next;pH2 = pH2->next;}    return pH1; //返回第一次相遇点 }

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！