6 概率图模型

文章目录

• 1 概率图模型的联合概率分布
• • 场景描述
  • 写出图6.1(a)中贝叶斯网络的联合概率分布?
  • 图6.1(b)中马尔可夫网络的联合概率分布?
• 2 概率图表示
• • 场景描述
  • 解释朴素贝叶斯模型的原理,并给出概率图模型表示。
  • 最大熵模型原理,并给出概率图模型表示
• 3生成式模型与判别式模型
• • 常见的概率图模型中,哪些是生成式,判別式?
• 4 马尔可夫模型
• • 对中文分词用隐马模型建模和训练?
  • 2 最大熵马尔可夫模型为什么会产生标注偏置问题?如何解决?

• 形容概率图模型,“优雅”。
• 对ー个实际问题,希望能挖掘隐含在数据中的知识。
• 概率图模型构建这样一幅图,用观测结点表示观测到的数据,
  • 隐含结点表示潜在的知识
  • 边来描述知识与数据的相互关系
  • 最后基于这样的关系图获得一个概率分布

• 概率图中的节点分
  • 隐含节点和观测节点,
  • 边分有向和无向
• 节点对应于随机变量,
• 边对应于随机变量的依赖或相关关系,
  • 有向表示单向依赖,
  • 无向边表示相互依赖

• 概率图模型分贝叶斯网络和马尔可夫网络
• 有向图
  • 无向图
• 概率图模型:
  • 朴素贝叶斯、最大熵、隐马、CRF、主题模型

1 概率图模型的联合概率分布

场景描述

• 概率图模型最“精彩”
  • 就是能够用简洁清晰的图表达概率生成的关系
• 而通过概率图还原其概率分布
  • 是概率图模型最重要的功能
• 根据贝叶斯网络和马尔可夫网络的概率图
  • 还原其联合概率分布。

写出图6.1(a)中贝叶斯网络的联合概率分布?

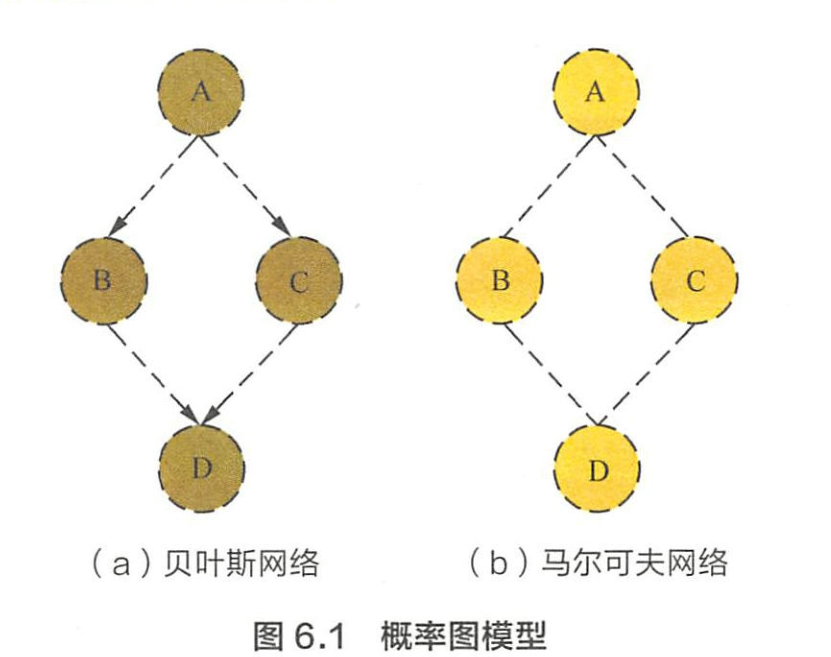
• 在给定A的条件下B和C条件独立
  • 可得

$$P(B,C|A)=P(C|A)P(B|A)$$

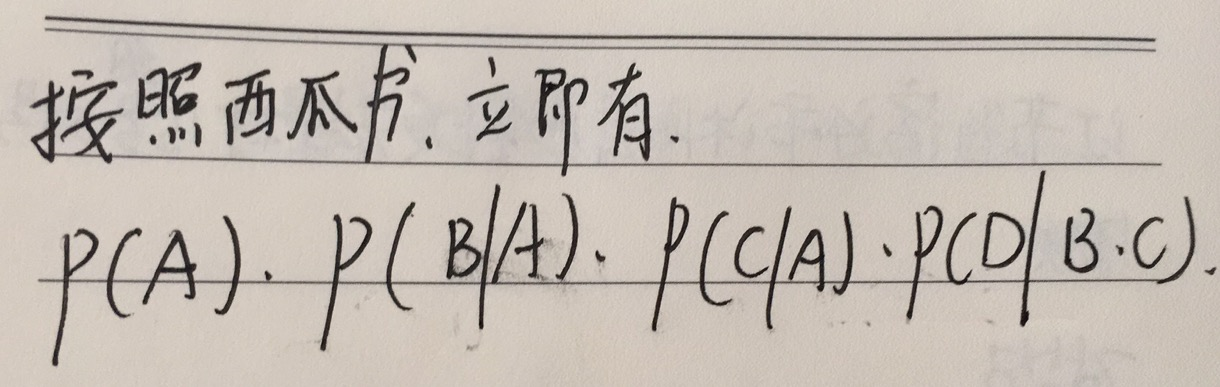
书上这里写的太啰嗦了

图6.1(b)中马尔可夫网络的联合概率分布?

• 马尔可夫网络中,联合概率分布的定义为

• C为图中最大团所构成的集合

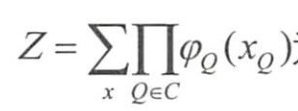
• 归ー化因子
• 是与团Q对应的势函数。
  • 非负,且应在概率较大的变量上取较大值
• 如

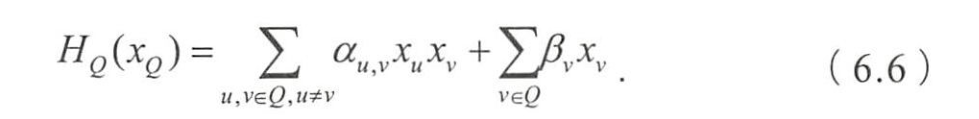
• 图6.1中,联合概率分布

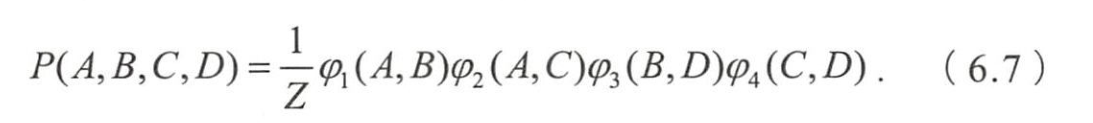
• 如果采用(6.5)作为势函数,则

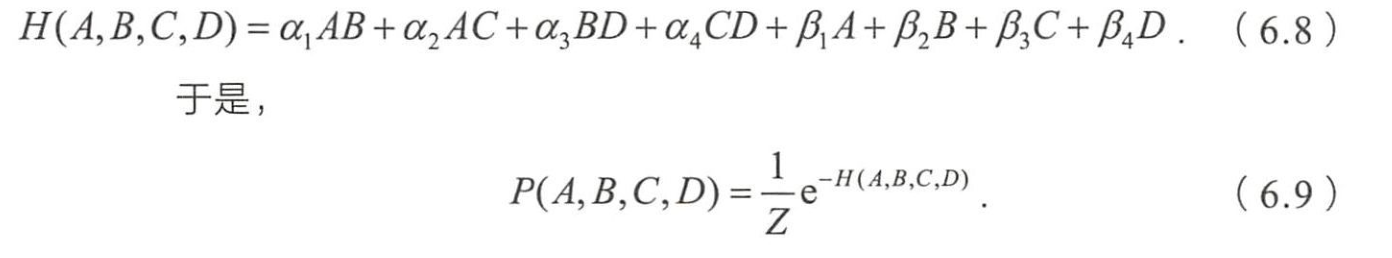
2 概率图表示

场景描述

• 上节通过概率图还原模型联合概率分布
• 考查面试者能否给出模型的概率图表示。

解释朴素贝叶斯模型的原理,并给出概率图模型表示。

• 朴素贝叶斯预测指定样本属于特定类别的概率 P ( y i ∣ x ) P(y_i|x) P(yi​∣x)
• 预测该样本的所属类别

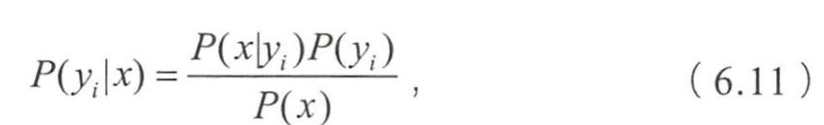
• x = ( x 1 , ⋯ , x n ) x=(x_1,\cdots,x_n) x=(x1​,⋯,xn​)为样本的特征向量
• $P(x)$为样本先验概率
• 设特征 x 1 , . . . , x n x_1,...,x_n x1​,...,xn​独立,可得

• P ( x 1 ∣ y i ) , P ( x 2 ∣ y i ) , . . . P(x_1|y_i),P(x_2|y_i),... P(x1​∣yi​),P(x2​∣yi​),...,及 P ( y i ) P(y_i) P(yi​)可通过训练样本统计得到
• 后验概率 P ( x j ∣ y i ) P(x_j|y_i) P(xj​∣yi​)的取值决定分类的结果
  • 我觉得，这不是后验概率，是似然哦！
  • 且任意特征 x j x_j xj​都由 y i y_i yi​所影响
• 因此可图6.2

• 图6.2的表示为盘式记法
• 如果变量$y$同时对 x 1 , x 2 , . . . x N x_1,x_2,...x_N x1​,x2​,...xN​这N个变量产生影响,
  • 则可简记成图6.2

最大熵模型原理,并给出概率图模型表示

• 信息是指人们对事物理解的不确定性的降低或消除,
  • 熵就是不确定性的度量,熵越大,不确定性也越大
  • 最大熵原理是概率模型学习的一个准则,在满足约束条件的模型集合中选取熵最大的模型,即不确定性最大的模型
  • 鸡蛋不能放在一个篮子里,就是指在事情具有不确定性的时候,我们倾向于尝试它的多种可能性,从而降低结果的风险。
  • 摸清事情背后的规律后,可加入一个约束,将不符合规律约束的情况排除,在剩下的可能性中去寻找使得熵最大的决策。

• 设离散随机变量$x$的分布是$P(x)$

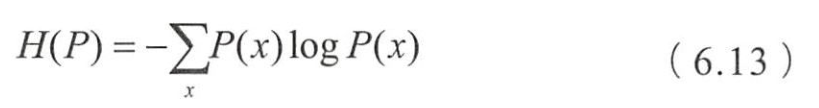
• 当$x$服从均匀分布时
  • 熵最大
  • 不确定性最高
• 离散随机变量$x$和$y$上的条件概率分布$P(y|x)$,
• 定义在条件概率上的条件熵为

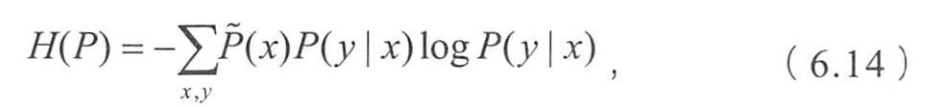
• 样本在训练数据集上的经验分布
  • 即$x$的各个取值在样本中出现的频率统计。

• 最大熵模型学习分布$P(y|x)$,使条件熵$H(P)$最大
• 在对训练数据集一无所知的情况下,最大熵模型认为$P(y|x)$均匀分布
• 有训练集后?
• 希望从中找到一些规律,消除不确定性,这时就用到特征函数
• 特征函数描述输入$x$和输出$y$之间的一个规律
  • 例如当x=y时,$f(x,y)$等于一个较大的正数。
  • 为使学习到的模型能正确捕捉训练数据集中的这一规律(特征)
  • 加入一个约束
  • 使特征函数关于经验分布的期望值与
  • 关于模型$P(y|x)$和经验分布$P(x)$的期望相等

• 特征函数关于经验分布的期望值

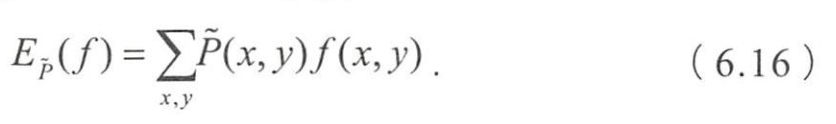
• 关于模型和经验分布的期望

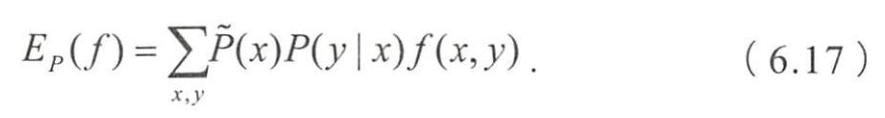
• 给定训练数据集 T = { ( x 1 , y 1 ) 、 ( x 2 , y 2 ) ⋯ ( x N , y N ) } T=\{(x_1,y_1)、(x_2,y_2)\cdots(x_N,y_N)\} T={(x1​,y1​)、(x2​,y2​)⋯(xN​,yN​)}
• 最大熵模型的学习等价于约東最优化

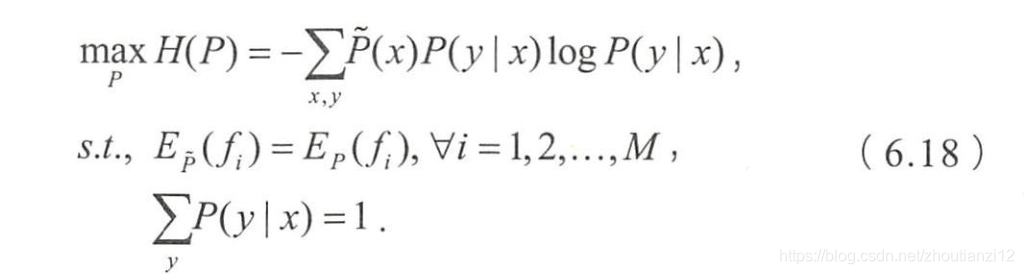
• 求解后可以得到最大熵模型的表达形式为

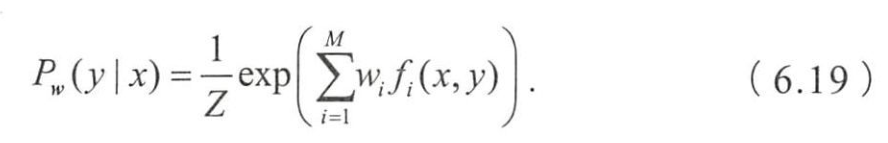
• 最大熵模型归结为学习最佳的参数$w$,使 P w ( y ∣ x ) P_w(y|x) Pw​(y∣x)最大化

• 概率图模型角度理解,
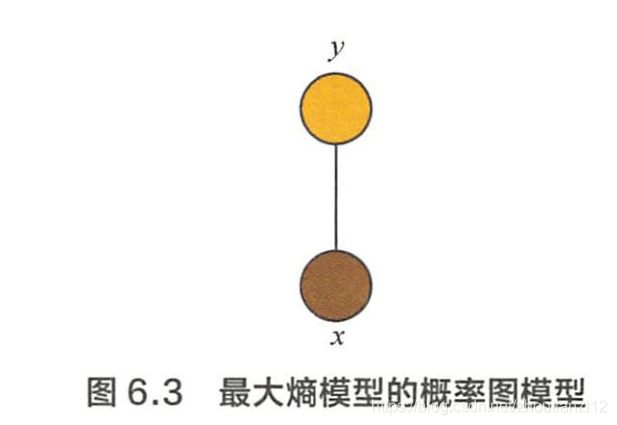
• P w ( y ∣ x ) P_w(y|x) Pw​(y∣x)的表达形式类似于势函数为指数函数的马尔可夫网络,
  • 变量$x$和$y$构成了ー个最大团,如图6.3

3生成式模型与判别式模型

常见的概率图模型中,哪些是生成式,判別式?

• 可观测到的变量集合$X$,要预测的变量集合$Y$,其他变量集合$Z$。
• 生成式模型是对联合概率分布$P(X,Y,Z)$建模
• 在给定观测集合$X$的条件下,通过计算边缘分布来得到对变量集合Y
  的推断,即

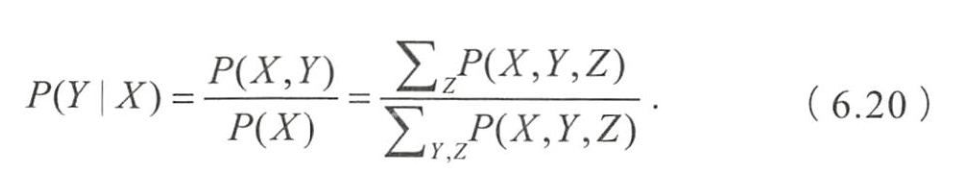
• 判别式模型是直接对条件概率分布$P(Y,Z|X)$建模,
  • 然后消掉无关变量Z就得到对变量集合Y的预测,即

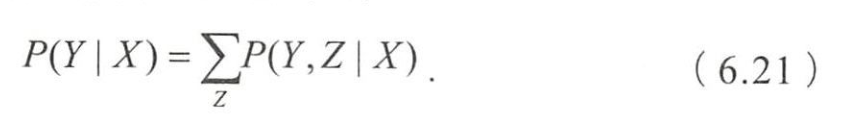
• 常见的概率图模型有朴素贝叶斯、最大熵模型、贝叶斯网络、隐马
  尔可夫模型、条件随机场、pLSA、LDA
• 朴素贝叶斯、贝叶斯网络、pLSA、LDA等模型都是先对联合概率分布建模,然后再通过计算边缘分布得到对变量的预测,属生成式模型;
• 最大熵模型是直接对条件概率分布建模,属判别式模型。
• 隐马和CRF是对序列数据进行建模的方法,
  • 其中隐马尔可夫模型属于生成式模型,
  • 条件随机场属于判别式模型。

4 马尔可夫模型

• 时间和状态的取值都是离散的马尔可夫过程称

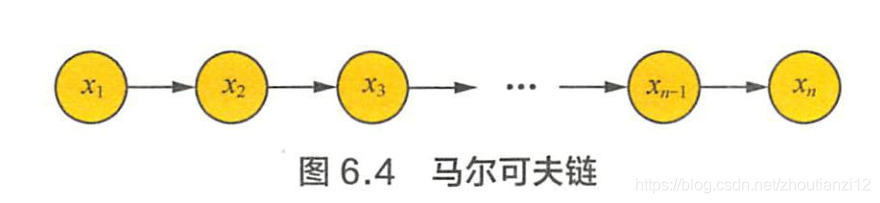
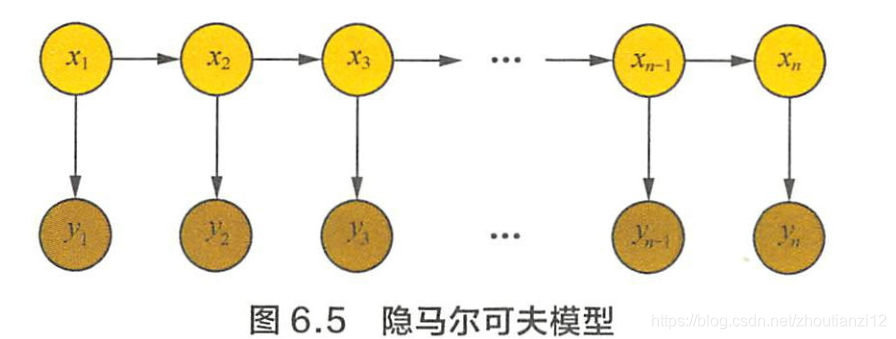
• 隐马模型是对含有未知参数(隐状态)的马尔可夫链建模的生成模型,概率图模型如图6.5

• 简单马尔可夫模型中,状态对于观测者都是可见的
  • 马尔可夫模型中仅包括状态间的转移概率
• 隐马中,隐状态 x i x_i xi​对观测者不可见
  • 能观测到的只有每个隐状态 x i x_i xi​对应的输出 y i y_i yi​
  • 观测状态 y i y_i yi​的概率分布仅取决于对应的隐状态 x i x_i xi​
  • 参数
    • 隐状态间的转移概率
    • 隐状态到观测状态的输出概率
    • 隐状态$x$的取值空间
    • 观测状态$y$的取值空间
    • 初始状态的概率分布

对中文分词用隐马模型建模和训练?

• 3个不同葫芦,每个葫芦有好和坏,现从3个葫芦中按以下规则倒出药

• (1)随机选一个葫芦

• (2)从葫芦里倒出一颗,记录好还是坏后将药放回

• (3)从当前葫芦依照一定的概率转移到下ー个

• (4)重复(2)和(3)

• 整个过程中,并不知道每次拿到的是哪一个葫芦。

• 用隐马模型来描述以上过程,

  • 隐状态就是当前是哪一个葫芦,
  • 隐状态的取值空间葫芦1,葫芦2,葫芦3},
  • 观测状态的取値空间{好 坏}
  • 初始状态的概率分布就是第(1)步随机挑选葫芦的概率分布,
  • 隐状态间的转移概率就是从当前葫芦转移到下一个葫芦的概率,
  • 隐状态到观测状态的输出概率就是每个葫芦里好药和坏药的概率。
  • 记录下来的药的顺序就是观测状态的序列,
    • 而每次拿到的葫芦的顺序就是隐状态的序列。

• 隐马模型三个基本问题

• (1)概率计算:已知所有参数,计算观测序列$Y$出现的概率

  • 前向和后向算法

• (2)预测问题:已知模型所有参数和观测序列$Y$,

  • 计算最可能的隐状态序列$X$
  • 动态规划算法————维特比算法

• (3)学习问题:已知观测序列$Y$,

  • 求解使得该观测序列概率最大的模型参数,
  • 包括隐状态序列、隐状态之间的转移概率分布
  • 从隐状态到观测状态的概率分布,
  • 可Baum-Welch算法参数学习
  • 是最大期望算法的一个特例。

• 隐马模型常用来解決序列标注问题,因此也可将分词问题转化为一个序列标注问题
• 可对中文句子中的每个字做以下标注
  • B表示一个词开头的第一个字
  • E表示一个词结尾的最后一个字
  • M表示一个词中间的字
  • S表示一个单字词
  • 则隐状态取值空间为{B,E,M,S}
  • 同时对隐状态的转移概率可给出一些先验知识,
    • B和M后面只能是M或E
    • S和E后面只能是B或S
  • 每个字就是模型中的观测状态,取值空间为语料中的所有中文字
  • 完成建模之后,用语料进行训练可分有监督和无监督训练
  • 有监督训练即对语料进行标注,
    • 相当于根据经验得到了语料的所有隐状态信息,
    • 然后就可以用简单的计数法来对模型中的概率分布进行极大似然估计。
  • 无监督训练可用上文提到的Baum-Welch,同时优化隐状态序列和模型对应的概率分布。

2 最大熵马尔可夫模型为什么会产生标注偏置问题?如何解决?

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！