python简单实验

一、汉诺塔问题

1. 解题
   1. 汉诺塔问题原理

      1. 汉诺塔问题是一个经典的数学谜题，给定三根柱子和一些不同大小的圆盘，目标是将所有圆盘从一根柱子上移动到另一根柱子上，同事要保持圆盘的顺序不变。在移动过程中，只能使用以下规则：

         1. 每次只能移动一个圆盘。
         2. 每根柱子上的圆盘必须按照从大到小的顺序摆放，且大圆盘不能放在小圆盘上面。
         3. 只能将圆盘移到空柱子或者比它大的圆盘上。

      2. 这个问题源自传说中的印度民间故事：在一个寺庙里，有三根针和64个大小不同的金盘。神预言，当所有的盘子都从一根针上转移到另一根针上时，世界将毁灭。所以这个问题也以汉诺塔（Hanoi Tower）命名。

2. Python代码

   1. def yidong(n):if  n == 1:return 1else:return 2 * yidong(n-1)+1n = int(input("移动块数："))
      a = yidong(n)print("移动步骤:%s" %a)input()

3.实现结果

二、跳楼梯问题

1. 解题
   1. 跳楼梯问题是一个经典的递归和动态规划问题。它的基本思想是，假设你站在一座楼梯前，这座楼梯有n个台阶。每次你可以选择跨1个台阶或者2个台阶跳下楼梯。问到达楼梯的顶部有多少种不同的方法。
      1. 如果你选择跨1个台阶，那么剩下的台阶数变为n-1，我们可以递归地计算从n-1个台阶跳到顶部的方法数。
      2. 如果你选择跨2个台阶，那么剩下的台阶数变为n-2，我们可以递归地计算从n-2个台阶跳到顶部的方法数。
2. 递归公式：f(n) = f(n-1) + f(n-2)，其中f(n)表示从第n个台阶跳到顶部的方法数。
3. Python代码

   1. def louti(n):if n == 1:return 1elif n== 2:return 2else :return louti(n-1) + louti(n-2)n = int(input("请输入要上去的楼梯数量："))
      a = louti(n)print("需要走的步骤有：%s" %a)

4. 实现结果

三、水仙花数问题

1. 解题
   1. 水仙花数，也被称为自恋数、阿姆斯特朗数，是指一个n位数，它的每个位上的数字的n次幂之和等于它本身。例如，一个3位数153就是一个水仙花数，因为1^3 + 5^3 + 3^3 = 153。
   2. 水仙花数问题是一个经典的数学问题，其基本思路是使用循环和条件判断来判断一个数是否为水仙花数。一般来说，可以按以下步骤解决该问题：
      1. 从一个给定的范围（如1到1000）遍历每个数。
      2. 对于每个数，我们需要确定它有多少位数。可以通过将其转换为字符串，并计算字符串的长度来得到。
      3. 将该数按照位数进行分解，可以使用取模和除法来获取每个位上的数字。
      4. 对每个位上的数字进行n次幂计算，并将结果累加起来。
      5. 将累加的结果与原始数进行比较，如果相等，则该数为水仙花数。
      6. 如果想要找到给定范围内的所有水仙花数，可以将上述步骤放入一个循环中，逐个检查每个数是否为水仙花数，并将结果保存起来。
2. Python代码

   for i in range(100,1000):hundreds = i // 100 #获取百位数tens = (i % 100) // 10     # 获取十位数   							# 获取个位数ones = i % 10    # 获取个位数def shuixianhua(i):  #判断一个数是否为水仙花数的函数if hundreds**3 + tens**3 +ones**3 == i:return ielse :return a = shuixianhua(i)if a == None:   #定义如果函数返回None时，不输出值continueelse :print("水仙花数为：%s" %a)input()

3. 结果

四、验证:任意一个大于9的整数减去它的个位数字之和所得的差,一定能被9整除.

1. 解题
   1. 先将一个数的各个位数之和求出
   2. 通过判断语句对这个数能否支持这个命题进行判断
   3. 打印结果
2. Python代码

   a = int(input("请输入一个大于9的数字："))if a <= 9:print("请重新输入")
   else:def sum_of_digits(a):total = 0while a > 0:total += a % 10a //= 10return totaldef determine(total):if (a - total) % 9 == 0:return 1else:return 0total = sum_of_digits(a)
   c = determine(total)if c == 1:print("true")
   else:print("false")input()

3. 结果

五、 一个五位数,若在它的后面写上一个7,得到一个六位数A,若在它前面写上一个7,得到一个六位数B,B是A的五倍,求此五位数.

1. 解题
   1. 先使用循环遍历五位数
   2. 求出五位数前面加上7和后面加上7的值
   3. 进行判断求出值
2. Python代码

   
   for i in range(10000,100000):a = 10*i + 7b = i + 700000if b/a == 5:print(i)else :continue
   print("判断完成")input()
   

3. 结果

六、求1~100之间不能被3整除的数之和

1. 解题
   1. 遍历1到100 之间的数字
   2. 判断被三能整除的数字
   3. 将其加和
2. Python代码

   a = 0
   for i in range(1,101):if i%3 != 0:a += i else :continue
   print("和等于%s"%a)input()

   3.结果

七、输入数，判断这个数是否是质数（要求使用函数 + for循环）

1. 解题
   1. 了解质数定义
   2. 使用input接入输入值
   3. 根据函数定义使用for循环判断结果
   4. 将输出结果打印出来
2. Python代码

   a = int(input("请输入一个数字："))
   def panduan(a):if a == 0:print("重新输入")else :for i in range(2, a):if a % i == 0:print("不是质数")breakelse:print("是质数")breakpanduan(a)
   

   3.结果

八、求50~150之间的质数是那些？

1. 解题
   1. 在七的基础上加上for循环遍历
2. Python代码

   def panduan(a):if a == 0:print("重新输入")else :for i in range(2, a):if a % i == 0:breakelse:print(a,end = "  ")breakfor a in range(50,151):panduan(a)input()

3. 结果

九、给定一个正整数N,找出1到N（含）之间所有质数的总和

1. 解题
   1. 在将七和八结合起来
2. python代码

   def panduan(a):if a == 0:return 0else:for i in range(2, a):if a % i == 0:return 0return ab = 0
   num = int(input("请输入一个数："))for a in range(1, num):c = panduan(a)b += cprint(b)

3. 结果

十、计算PI（公式如下：PI＝4（1－1/3+1/5-1/7+1/9-1.......）

1. 解题
   1. 使用函数和for循环
   2. 通过for循环写出等差数列
   3. 控制变量符号
   4. 组合成公式并且打印出来
2. Python代码

   def PI(n):d = 0f = 2 * n + 1for i in range(f):a = 1 / (2*i + 1)  # 修改为正确的计算公式b = (-1) ** i  # 修改为正确的计算公式c = a * bd += creturn d * 4n = int(input("请输入PI的运算次数："))
   e = PI(n)
   print("PI的值：%s" % e)

   3.结果

十一、 求a+aa+aaa+.......+aaaaaaaaa=?其中a为1至9之中的一个数，项数也要可以指定

1. 解题
   1. if判断引导输入正确的值
   2. 构建每项数
   3. 将每项数字加和
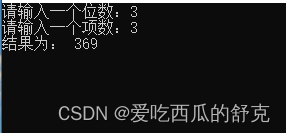
2. Python代码

   a = int(input("请输入一个位数："))
   n = int(input("请输入一个项数："))
   sum = 0
   c = 0
   if a >= 10:print("请输入小于10的位数")
   else:for i in range(1, n+1):sum += a * (10**(i-1))c += sumprint("结果为：", c)

3. 结果

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！