最小直径生成树
最小直径生成树
其实就是找树的绝对中心(到其他节点的最大距离最小,可证直径为绝对中心到其他节点最远距离乘2,也就是说直径两端点到绝对中心距离相等,且绝对中心可能在边上)。
求绝对中心
枚举边,假设绝对中心在该边(u,v)上,边长L,设其到u的距离为x,则直径的1/2应为 m a x ( d [ u ] [ i ] + x , d [ v ] [ i ] + L − x ) max(d[u][i]+x,d[v][i]+L-x) max(d[u][i]+x,d[v][i]+L−x),其图像如下(盗的图),要与max所以图像为实现部分,那么我们要找的值就是最低点所对应的,我们先对 d [ u ] [ i ] d[u][i] d[u][i]排序,只有当 d [ v ] [ i ] > d [ v ] [ l a s t ] , l a s t 指 上 一 次 满 足 条 件 的 i d[v][i]>d[v][last],last指上一次满足条件的i d[v][i]>d[v][last],last指上一次满足条件的i,才有可能取最小值,此时直径1/2 为 d [ v ] [ l a s t ] + L − x 或 d [ u ] [ i ] + x d[v][last]+L-x或d[u][i]+x d[v][last]+L−x或d[u][i]+x,所以直径 d [ v ] [ l a s t ] + d [ u ] [ i ] + w ( u , v ) d[v][last]+d[u][i]+w(u,v) d[v][last]+d[u][i]+w(u,v).
附上盗的图,好多博客都有。
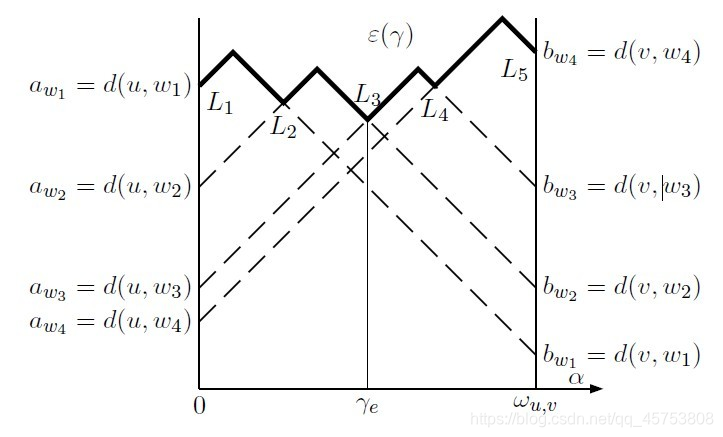
求最小直径生成树
求最小直径生成树
求出绝对中心,若在边上,给两个端点附上初始距离,再跑最短路径生成树即可。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!