贪心算法 —— 排队打水问题1

1319：【例6.1】排队接水

时间限制: 1000 ms 内存限制: 65536 KB
提交数: 11724 通过数: 5192
【题目描述】
有n个人在一个水龙头前排队接水，假如每个人接水的时间为Ti，请编程找出这n个人排队的一种顺序，使得n个人的平均等待时间最小。

【输入】
共两行，第一行为n(1≤n≤1000)；第二行分别表示第1个人到第n个人每人的接水时间T1，T2，…，Tn，每个数据之间有1个空格。

【输出】
有两行，第一行为一种排队顺序，即1到n的一种排列；第二行为这种排列方案下的平均等待时间(输出结果精确到小数点后两位)。

【输入样例】
10
56 12 1 99 1000 234 33 55 99 812
【输出样例】
3 2 7 8 1 4 9 6 10 5
291.90

这是一道经典的贪心问题。
贪心问题一般的思路都是让每一步都是最优的解决方案，然后由局部影响全局，是的全局为最优解
当然贪心问题不能对每一道题都有这样的作用，不过对于本体来说已经足够了

我们看一下题目的意思，一个水龙头，n个人排队打水，要求得出所有人排队打水，总的等待时长最小，并求出平均等待时长。
这无非是让我们进行一种排序，使得结果的总和最小。

我们首先来模拟一下样例
首先打水的时候是不计入排队等待的时间的，这是当然的，我都已经接到水了，我还拍个什么队啊呀。
所以第一个人的排队时间为0
第二个接水的人要等待第一个人接完水之后才能接到水，所以他的等待时间为第一个人的接水时间，即56
然后就是第三个人了，他前面由两个人，第一个接水的和第二个接水的，所以他要等待的时间为前两个人接水的时间之和，即**（56+12）**
然后···················
当到了最后两个人，即第n-1个接水，第n个人等待，则要等待前（n-2）个人，则他的等待时间为前面（n-2）个人的时间和
到了最后一个，他已经等了前面的所有人，是最苦逼的一个，不过谁让他是最后一个呢。

我们可以看到，当第一个人打水的时候，剩下的（n-1)个人都要等着，当第二个人打水的时候剩下的人还是要等着，一共有（n-2）个人在等着，等第二个人的时间总和为第二个人打水的时间乘以（n-2）以此类推，我们可以得到我们要求的所有等待时间之和。
**a[1](n-1) + a[2](n-2) + a[3]*(n-3)+···a[n-1]1 + a[n]0;

我们可以看到，第一个打水的时候，是等待人数最多的时候，然后依次减小，所以我们就想了，怎样使排队的总时间最小呢，
答案当然是，让越靠前的人的打水的时间越短不就可以了。
即，我们将问题转化为：将打水的按时间长短时间进行一个从小到大的排序，使这个序列为递增序列。

我们感觉这样做是对的，但是我们怎么去证明呢。

我们知道，a和b这两个数只有两种排序方法，要么是a，b要么是b，a，我们要在这两种方案内找到是排队打水等待时间更少的一种方案。
下面我们来看一下哪一种方案更合适

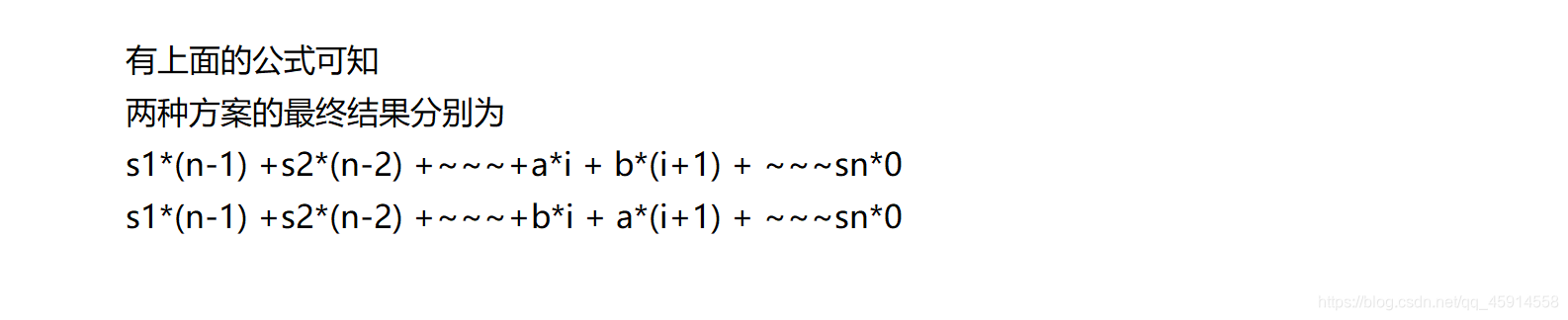
我们整理的

因为a>b 所以我们可以看出上面的式子比下面的式子的总值要大，而我们要的却是第二种情况，总值更小的那种情况
所以我们可以知道，将b放在a的前面，小数放在大数的前面，这正是我们前面推到的结论，将数列排成一个单调递增的而数列。

好啦，我感觉我讲的是非常详细的啦

下面就不再多说，给大家附上我的代码，来帮助大家理解

#include //万能头文件就是它
using namespace std;const int N = 1010;int n;struct fun{int a;//输入的数 int b;//下标 
}s[N];bool cmp(fun x, fun y){return x.a < y.a;//将结构题进行排序 
}
int main(){cin >> n;for(int i = 1; i <= n; i ++ ) cin >> s[i].a, s[i].b = i;sort(s + 1, s + 1 + n,cmp);//调用函数，实现排序 for (int i = 1; i <= n; i ++ ) {cout << s[i].b <<' ';}cout << endl;double sum = 0;for (int i = 1; i <= n; i ++ ){sum += s[i].a * (n - i);//公式的应用 }printf("%.2lf\n", sum / n);return 0;}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！