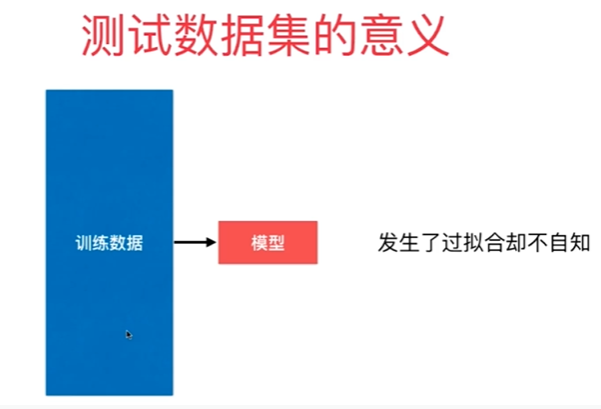
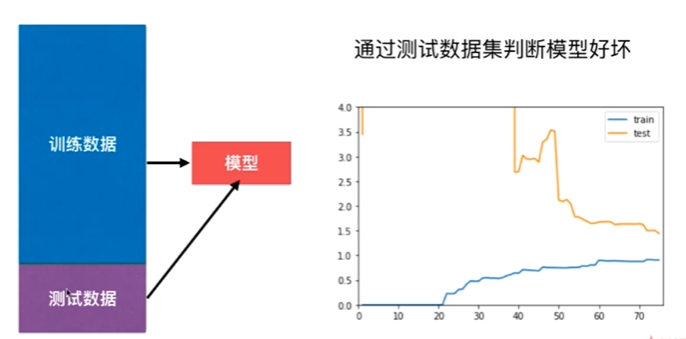
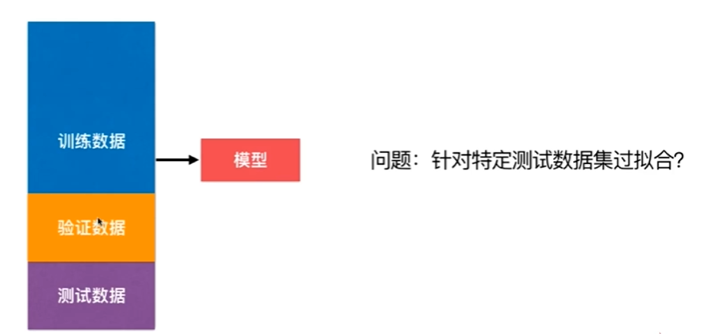
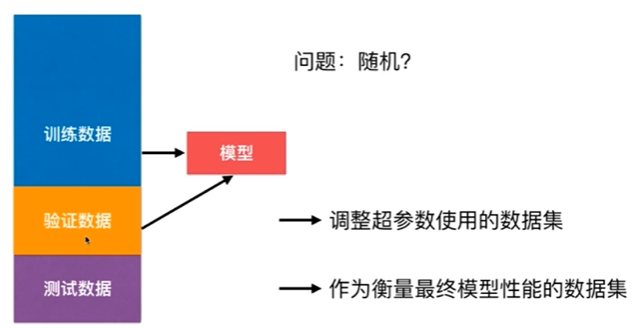
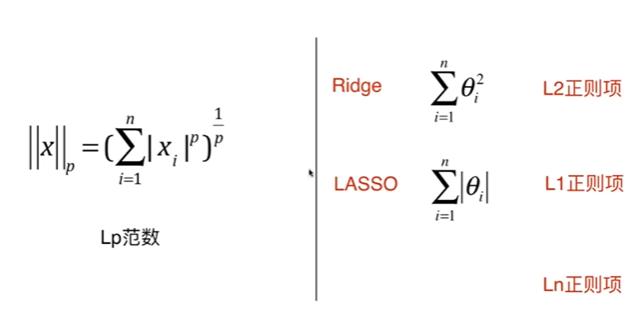8-6 验证数据集与交叉验证


Nnotbook 示例
Notbook 源码
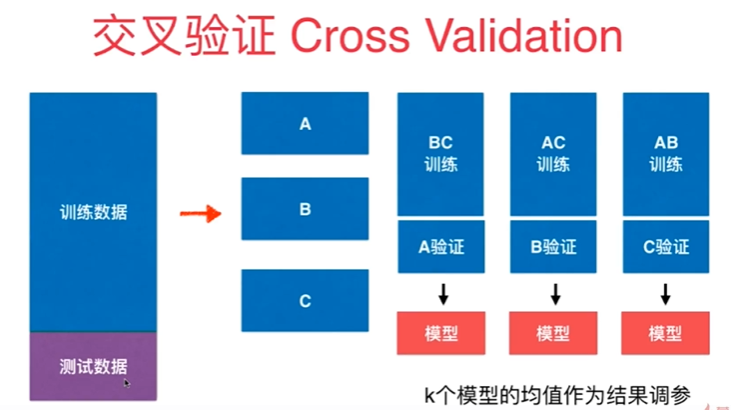
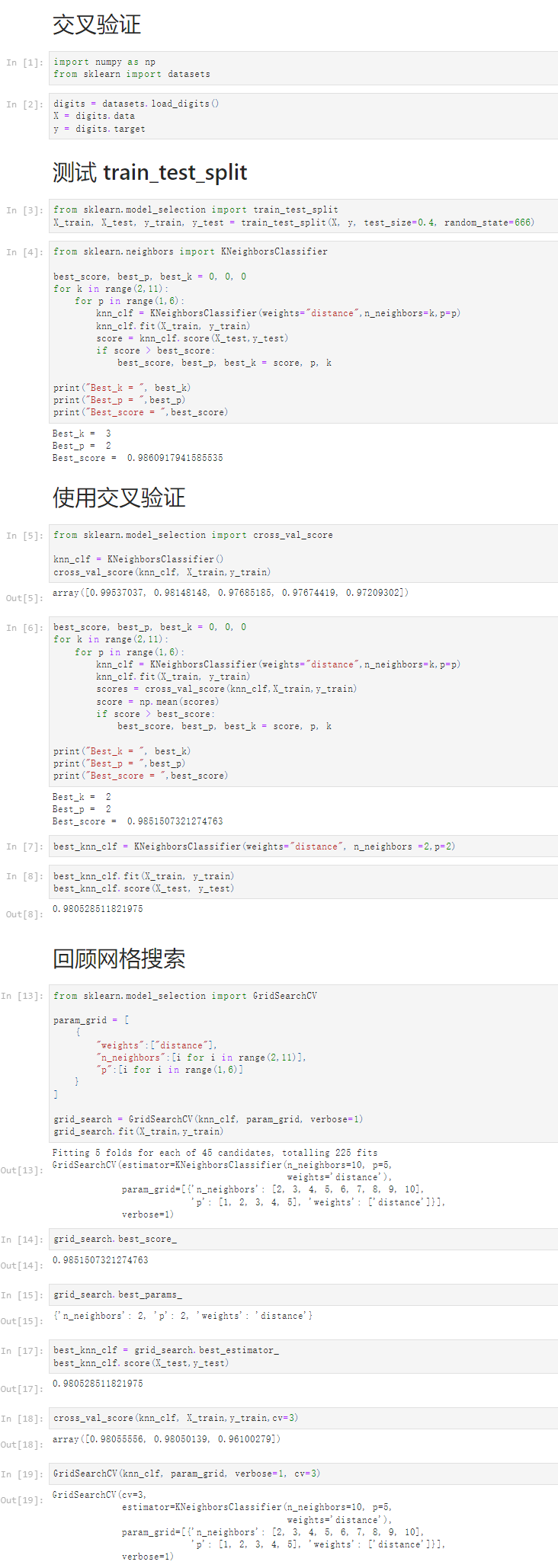
交叉验证
[1]
import numpy as np
from sklearn import datasets
[2]
digits = datasets.load_digits()
X = digits.data
y = digits.target
测试 train_test_split
[3]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=666)
[4]
from sklearn.neighbors import KNeighborsClassifierbest_score, best_p, best_k = 0, 0, 0
for k in range(2,11):for p in range(1,6):knn_clf = KNeighborsClassifier(weights="distance",n_neighbors=k,p=p)knn_clf.fit(X_train, y_train)score = knn_clf.score(X_test,y_test)if score > best_score:best_score, best_p, best_k = score, p, kprint("Best_k = ", best_k)
print("Best_p = ",best_p)
print("Best_score = ",best_score)
Best_k = 3
Best_p = 2
Best_score = 0.9860917941585535使用交叉验证
[5]
from sklearn.model_selection import cross_val_scoreknn_clf = KNeighborsClassifier()
cross_val_score(knn_clf, X_train,y_train)
array([0.99537037, 0.98148148, 0.97685185, 0.97674419, 0.97209302])
[6]
best_score, best_p, best_k = 0, 0, 0
for k in range(2,11):for p in range(1,6):knn_clf = KNeighborsClassifier(weights="distance",n_neighbors=k,p=p)knn_clf.fit(X_train, y_train)scores = cross_val_score(knn_clf,X_train,y_train)score = np.mean(scores)if score > best_score:best_score, best_p, best_k = score, p, kprint("Best_k = ", best_k)
print("Best_p = ",best_p)
print("Best_score = ",best_score)
Best_k = 2
Best_p = 2
Best_score = 0.9851507321274763[7]
best_knn_clf = KNeighborsClassifier(weights="distance", n_neighbors =2,p=2)
[8]
best_knn_clf.fit(X_train, y_train)
best_knn_clf.score(X_test, y_test)
0.980528511821975
回顾网格搜索
[13]
from sklearn.model_selection import GridSearchCVparam_grid = [{"weights":["distance"],"n_neighbors":[i for i in range(2,11)],"p":[i for i in range(1,6)]}
]grid_search = GridSearchCV(knn_clf, param_grid, verbose=1)
grid_search.fit(X_train,y_train)
Fitting 5 folds for each of 45 candidates, totalling 225 fitsGridSearchCV(estimator=KNeighborsClassifier(n_neighbors=10, p=5,weights='distance'),param_grid=[{'n_neighbors': [2, 3, 4, 5, 6, 7, 8, 9, 10],'p': [1, 2, 3, 4, 5], 'weights': ['distance']}],verbose=1)
[14]
grid_search.best_score_
0.9851507321274763
[15]
grid_search.best_params_
{'n_neighbors': 2, 'p': 2, 'weights': 'distance'}
[17]
best_knn_clf = grid_search.best_estimator_
best_knn_clf.score(X_test,y_test)
0.980528511821975
[18]
cross_val_score(knn_clf, X_train,y_train,cv=3)
array([0.98055556, 0.98050139, 0.96100279])
[19]
GridSearchCV(knn_clf, param_grid, verbose=1, cv=3)
GridSearchCV(cv=3,estimator=KNeighborsClassifier(n_neighbors=10, p=5,weights='distance'),param_grid=[{'n_neighbors': [2, 3, 4, 5, 6, 7, 8, 9, 10],'p': [1, 2, 3, 4, 5], 'weights': ['distance']}],verbose=1)
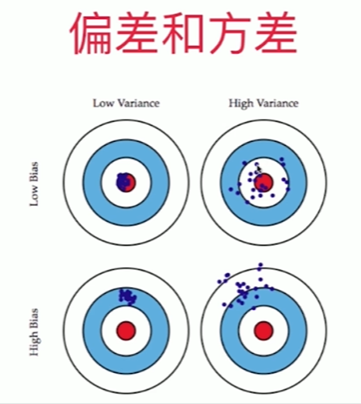
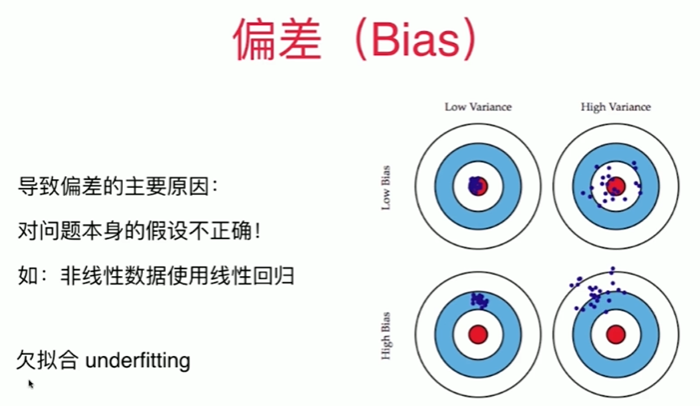
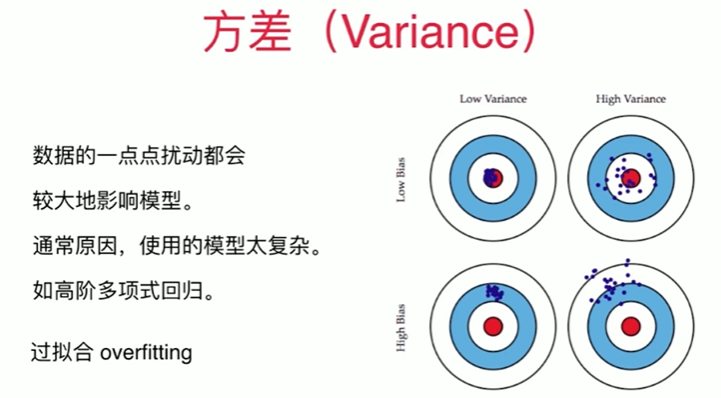
8-7 偏差方差平衡







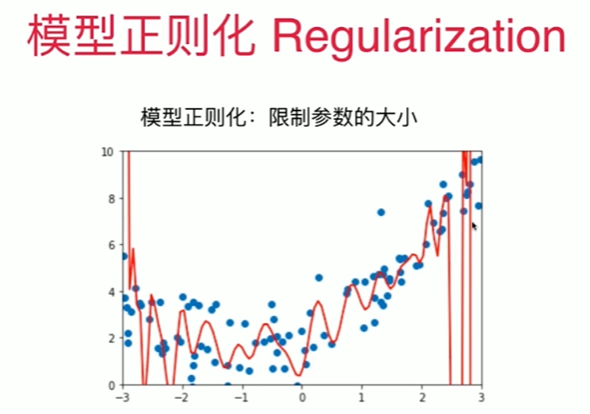
8-8 模型泛化与岭回归

Notbook 示例

Notbook 源码
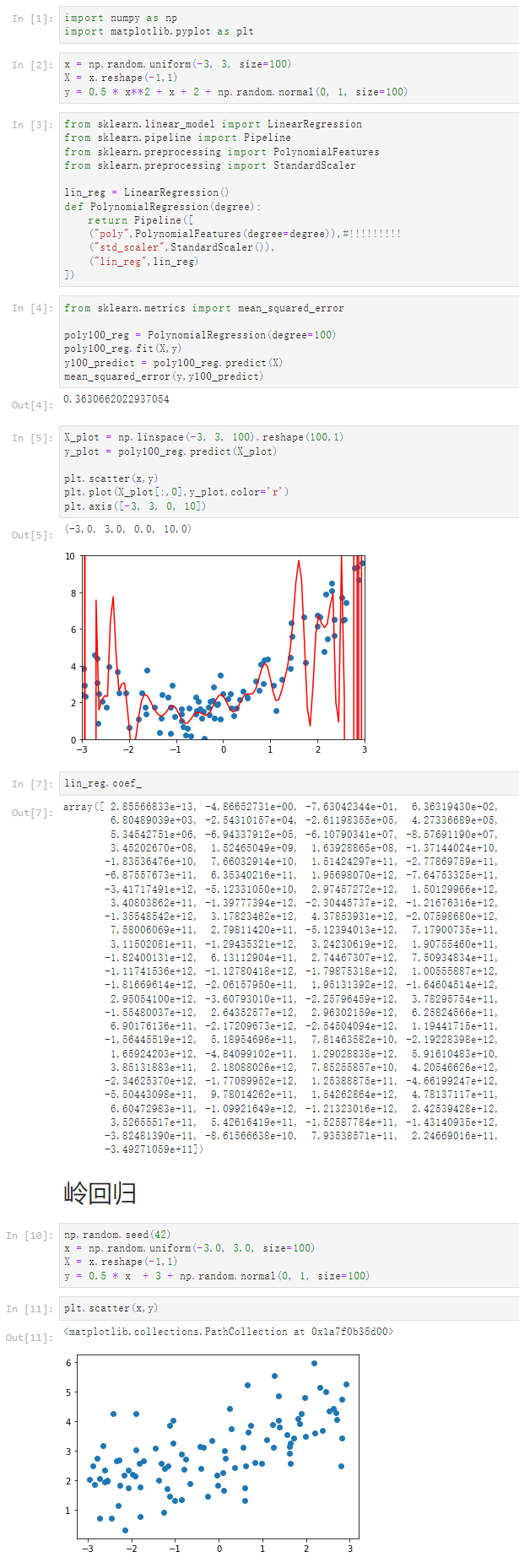
[1]
import numpy as np
import matplotlib.pyplot as plt
[2]
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1,1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
[3]
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScalerlin_reg = LinearRegression()
def PolynomialRegression(degree):return Pipeline([("poly",PolynomialFeatures(degree=degree)),#!!!!!!!!!("std_scaler",StandardScaler()),("lin_reg",lin_reg)
])
[4]
from sklearn.metrics import mean_squared_errorpoly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X,y)
y100_predict = poly100_reg.predict(X)
mean_squared_error(y,y100_predict)
0.3630662022937054
[5]
X_plot = np.linspace(-3, 3, 100).reshape(100,1)
y_plot = poly100_reg.predict(X_plot)plt.scatter(x,y)
plt.plot(X_plot[:,0],y_plot,color='r')
plt.axis([-3, 3, 0, 10])
(-3.0, 3.0, 0.0, 10.0)[7]
lin_reg.coef_
array([ 2.85566833e+13, -4.86652731e+00, -7.63042344e+01, 6.36319430e+02,6.80489039e+03, -2.54310157e+04, -2.61198355e+05, 4.27336689e+05,5.34542751e+06, -6.94337912e+05, -6.10790341e+07, -8.57691190e+07,3.45202670e+08, 1.52465049e+09, 1.63928865e+08, -1.37144024e+10,-1.83536476e+10, 7.66032914e+10, 1.51424297e+11, -2.77869759e+11,-6.87557673e+11, 6.35340216e+11, 1.95698070e+12, -7.64753325e+11,-3.41717491e+12, -5.12331050e+10, 2.97457272e+12, 1.50129966e+12,3.40803862e+11, -1.39777394e+12, -2.30445737e+12, -1.21676316e+12,-1.35548542e+12, 3.17823462e+12, 4.37853931e+12, -2.07598680e+12,7.58006069e+11, 2.79811420e+11, -5.12394013e+12, 7.17900735e+11,3.11502081e+11, -1.29435321e+12, 3.24230619e+12, 1.90755460e+11,-1.82400131e+12, 6.13112904e+11, 2.74467307e+12, 7.50934834e+11,-1.11741536e+12, -1.12780418e+12, -1.79875318e+12, 1.00555887e+12,-1.81669614e+12, -2.06157950e+11, 1.95131392e+12, -1.64604514e+12,2.95054100e+12, -3.60793010e+11, -2.25796459e+12, 3.78295754e+11,-1.55480037e+12, 2.64352577e+12, 2.96302159e+12, 6.25824566e+11,6.90176136e+11, -2.17209673e+12, -2.54504094e+12, 1.19441715e+11,-1.56445519e+12, 5.18954696e+11, 7.81463582e+10, -2.19228398e+12,1.65924203e+12, -4.84099102e+11, 1.29028838e+12, 5.91610483e+10,3.85131883e+11, 2.18088026e+12, 7.85255857e+10, 4.20546626e+12,-2.34625370e+12, -1.77089952e+12, 1.25388875e+11, -4.66199247e+12,-5.50443098e+11, 9.78014262e+11, 1.54262864e+12, 4.78137117e+11,6.60472983e+11, -1.09921649e+12, -1.21323016e+12, 2.42539428e+12,3.52655517e+11, 5.42616419e+11, -1.52587784e+11, -1.43140935e+12,-3.82481390e+11, -8.61566638e+10, 7.93538571e+11, 2.24669016e+11,-3.49271059e+11])
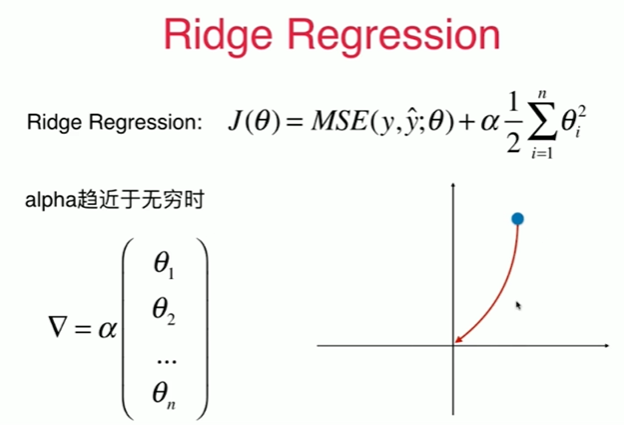
岭回归
[10]
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1,1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
[11]
plt.scatter(x,y)
岭回归
[1]
import numpy as np
import matplotlib.pyplot as plt
[2]
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1,1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
[3]
plt.scatter(x,y)
[4]
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScalerdef PolynomialRegression(degree):return Pipeline([("poly",PolynomialFeatures(degree=degree)),#!!!!!!!!!("std_scaler",StandardScaler()),("lin_reg",LinearRegression())
])
[5]
from sklearn.model_selection import train_test_splitnp.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
[6]
from sklearn.metrics import mean_squared_errorpoly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train,y_train)y_poly_predict = poly_reg.predict(X_test)
mean_squared_error(y_test,y_poly_predict)
167.9401086187559
[7]
X_plot = np.linspace(-3, 3, 100).reshape(100,1)
y_plot = poly_reg.predict(X_plot)plt.scatter(x,y)
plt.plot(X_plot[:,0],y_plot,color='r')
plt.axis([-3, 3, 0, 10])
(-3.0, 3.0, 0.0, 10.0)[8]
def plot_model(model):X_plot = np.linspace(-3, 3, 100).reshape(100,1)y_plot = model.predict(X_plot)plt.scatter(x,y)plt.plot(X_plot[:,0],y_plot,color='r')plt.axis([-3, 3, 0, 10])plot_model(poly_reg)使用岭回归
[9]
from sklearn.linear_model import Ridgedef RidgeRegression(degree, alpha):return Pipeline([("poly",PolynomialFeatures(degree=degree)),("std_scaler",StandardScaler()),("lin_reg",Ridge(alpha=alpha))])
[10]
ridg1_reg = RidgeRegression(20,0.0001)
ridg1_reg.fit(X_train,y_train)y1_predict = ridg1_reg.predict(X_test)
mean_squared_error(y_test,y1_predict)
1.323349275399316
[11]
plot_model(ridg1_reg)[13]
ridg2_reg = RidgeRegression(20,1)
ridg2_reg.fit(X_train,y_train)y2_predict = ridg2_reg.predict(X_test)
mean_squared_error(y_test,y2_predict)
1.1888759304218464
[14]
plot_model(ridg2_reg)[16]
ridg3_reg = RidgeRegression(20,100)
ridg3_reg.fit(X_train,y_train)y3_predict = ridg3_reg.predict(X_test)
mean_squared_error(y_test,y3_predict)
1.31964561130862
[17]
plot_model(ridg3_reg)[18]
ridg4_reg = RidgeRegression(20,1000000000)
ridg4_reg.fit(X_train,y_train)y4_predict = ridg4_reg.predict(X_test)
mean_squared_error(y_test,y4_predict)
1.8408934818370333
[19]
plot_model(ridg4_reg)
8-9 LASSO



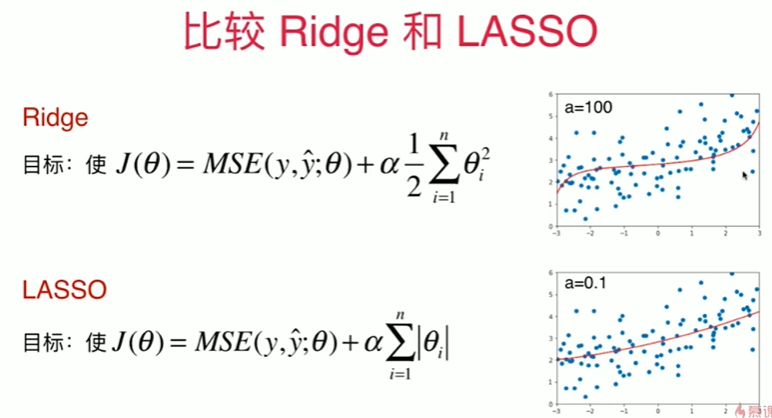


Notbook 示例

Notbook 源码
LASSO
[1]
import numpy as np
import matplotlib.pyplot as plt
[2]
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1,1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
[3]
plt.scatter(x,y)
[4]
from sklearn.model_selection import train_test_splitnp.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
[5]
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScalerdef PolynomialRegression(degree):return Pipeline([("poly",PolynomialFeatures(degree=degree)),#!!!!!!!!!("std_scaler",StandardScaler()),("lin_reg",LinearRegression())
])
[6]
from sklearn.metrics import mean_squared_errorpoly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train,y_train)y_poly_predict = poly_reg.predict(X_test)
mean_squared_error(y_test,y_poly_predict)
167.9401086187559
[7]
def plot_model(model):X_plot = np.linspace(-3, 3, 100).reshape(100,1)y_plot = model.predict(X_plot)plt.scatter(x,y)plt.plot(X_plot[:,0],y_plot,color='r')plt.axis([-3, 3, 0, 10])plot_model(poly_reg)LASSO
[8]
from sklearn.linear_model import Lassodef LassoRegression(degree, alpha):return Pipeline([("poly",PolynomialFeatures(degree=degree)),("std_scaler",StandardScaler()),("lin_reg", Lasso(alpha=alpha))])
[10]
lasso1_reg = LassoRegression(20, 0.01)
lasso1_reg.fit(X_train,y_train)y1_predict = lasso1_reg.predict(X_test)
mean_squared_error(y_test,y1_predict)
1.1496080843259961
[11]
plot_model(lasso1_reg)[13]
lasso2_reg = LassoRegression(20, 0.1)
lasso2_reg.fit(X_train,y_train)y2_predict = lasso2_reg.predict(X_test)
mean_squared_error(y_test,y2_predict)
1.1213911351818648
[14]
plot_model(lasso2_reg)[15]
lasso3_reg = LassoRegression(20, 1)
lasso3_reg.fit(X_train,y_train)y3_predict = lasso3_reg.predict(X_test)
mean_squared_error(y_test,y3_predict)
1.8408939659515595
[16]
plot_model(lasso3_reg)
8-10 L1,L2和弹性网络
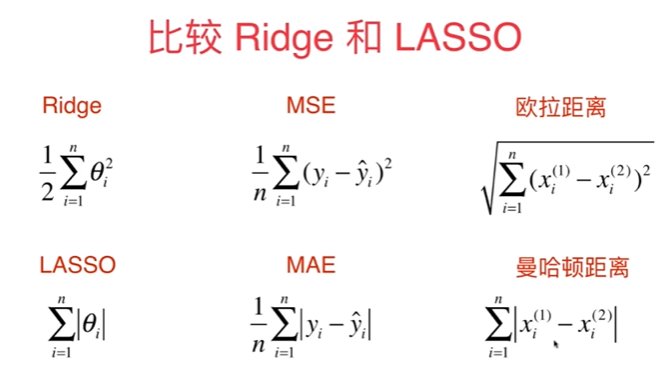

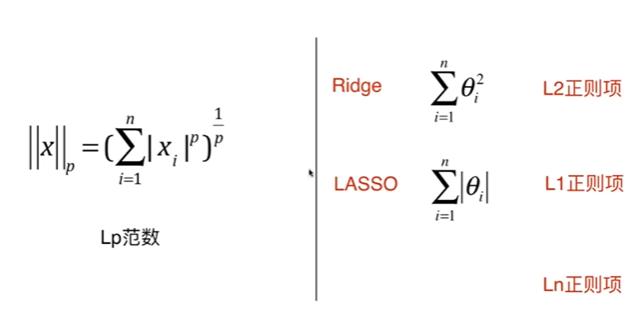



本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!