部分背包问题证明贪心算法正确性

部分背包问题

证明贪心算法的结构

第一步：符合贪心选择的特性（Greedy Choice Property）

我们需要证明我们的第一个选择（贪心选择 Greedy Choice，First Choice）包含在某些最优解中

第二步：符合归纳法结构（Inductive Structure）

我们需要证明第一个选择（贪心选择）之后，子问题和原问题还是同一类问题，意味着我们的选择不改变问题的结构，并且子问题的解可以和第一个选择（贪心选择）合并

第三步：最优子结构（Optimal Substructure）

如果我们可以最优的解决子问题，我们可以将子问题的解和贪心选择得到原问题的解

问题本身

输入：

• 个物品，每个物品有自身的重量和价值
• 1个背包，背包最多可以存放重量为的物品

前提：每个物品可以只取其中的一部分，比如拿0.5个某物品

输出：

• 在每个物品可以只取其中的一部分的前提下，使得背包内物品价值最大

定义我们的算法：

按照每个物品的密度给物品进行升序排列，然后从密度最高的物品开始选，如果空间不够存放一整个物品，就能存放多少部分这个物品就存放多少部分（Best fit）

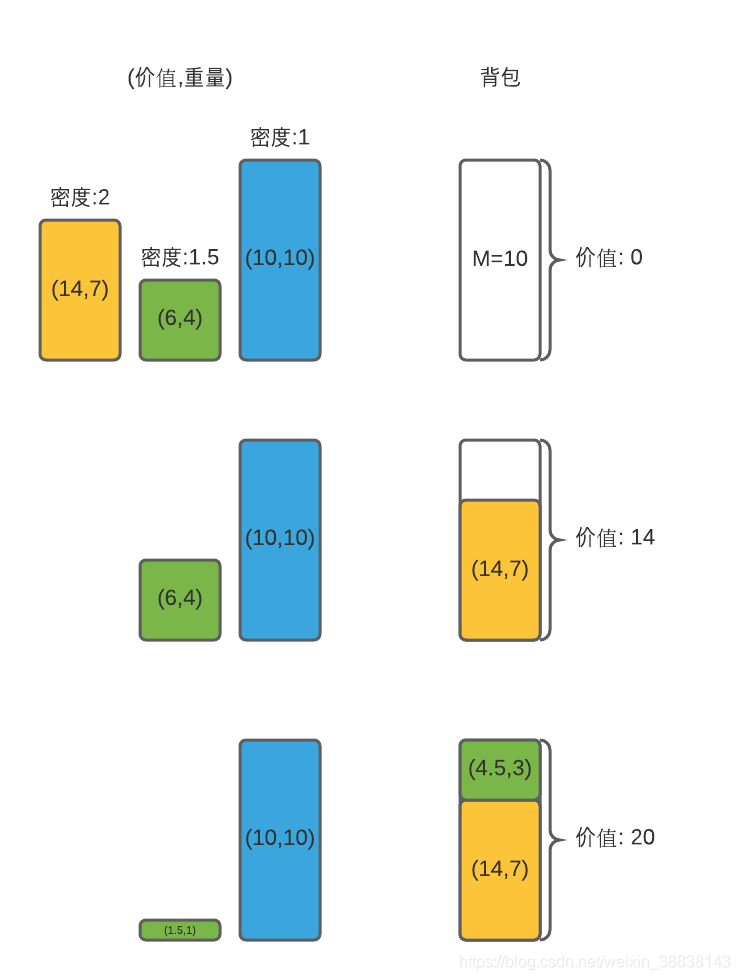
证明符合贪心选择的特性：

Claim：让物品为最高密度的物品，假设这里存在一个最优解用到了这么多重量的物品

证明：

让为最优解，

• 如果用到了多的物品，那么已经证明了我们的第一个选择（Greedy Choice，First Choice）包含在某些最优解中。
• 如果没有用到多的物品，那么我么可以将背包中任意一部分和物品进行交换，因为我们是按照物品密度排序，而且我们已经定义物品为最高密度的物品，所以与物品交换的物品必然比物品的密度要小，所以等量交换后，我们得到的解会比更优，这个结论与和为最优解的假设冲突，所以最优解中必然含有多的物品。因此符合贪心选择的特性（Greedy Choice Property）。

证明符合归纳法结构（Inductive Structure）

Claim：在完成第一个选择（贪心选择）之后，子问题和原问题还是同一类问题，意味着我们的选择不改变问题的结构，并且子问题的解可以和第一个选择（贪心选择）合并

证明：

• 子问题含有除了物品之外的所有物品，背包容量变成了，因此物品可以和子问题的解合并。

证明最优子结构（Optimal Substructure）

Claim：定义为原问题，为在完成第一个选择（贪心选择）之后的子问题，为子问题的最优解，那么为原问题的最优解

证明：

• 让为贪心选择（是）
• 那么

假设不是最优解，有一个其他的最优解，因为我们已经证明了算法符合贪心选择的特性，所以我们知道最优解中一定含有贪心选择

• 那么就应该是子问题的解
• 所以
• 但是这与为子问题的最优解的定义产生冲突，所以不可能不是最优解，因为为原问题的最优解。QED

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！