BP网络过程推演 完整过程及公式

BP(back propagation)网络，学习笔记，有不足或错误的以后继续增改

参考图

X输入数据

V输入层到隐层间的权重

B隐层的输出值

W隐层到输出层的权重

Y输出层的输出值

前向传播：

输出就是这个公式的结果

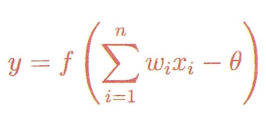
不多说了。

反向传播：

1  均方误差

想要学习反向传播，你得先知道均方误差。

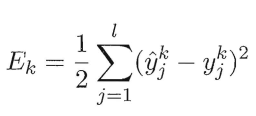
也就是预测和实际的一维向量每个位置对应相减的求平方，在相加的和的二分之一。

2  梯度

第二个就是梯度的计算，通过上面的方差和求得

xi                      yj                    zk                     dk

输入层             隐层               输出层               真实值

1/2为了去掉求导后的2

        从第三个式子可以看出y层的第j个节点(神经元)的残差等于z层与其所连接的所有节点(神经元)的残差与权值的乘值的和再乘以对该节点(y层的第j个节点)的导数。

        想象一下，反馈传播的思想，第一个残差是从输出层得出的（上面第二个公式），然后再传给隐层，一层一层的往前影响个层间权值和偏置。

         这里还要注意卷积层和卷积核的概念不要混淆，他们不都是层。

3  △权值

最后的权值和偏置的更新公式。原公式如下，经过带入替换后得出后面的

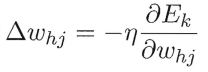
η就是学习率，这个式子就权值更新公式。负号表示了反向传播。均方误差与当前权值的导数（梯度项），再乘以学习率。

注意到叫Whj先影响到第 j 个输出层神经元的输入值岛，再影响到其输出值βj，然后影响到 Ek ，有

——————————————————————

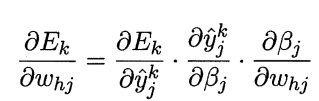
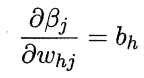输出层的输入值比上每对神经元间的权重，也就是bh隐层的输出值

——————————————————————

f是激活函数，对其求导。

再根据预测值和均方误差公式

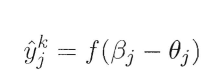
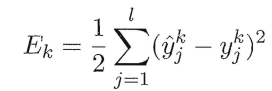
求出下面的梯度项

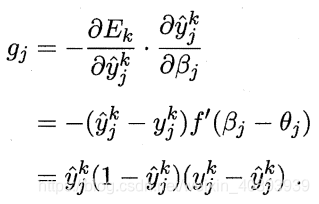
注意到最后一项即输出层的误差

——————————————————————

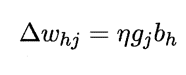
最后的ΔW求解公式也就成了这个形式，学习率*梯度项*上一层的输出值。

偏置计算过程类似

总结

所以说整个过程关键在于三个，一个是你得知道均方误差的计算，另一个就是残差的计算方法，最后是权值（偏置）更新公式。

人为可以调节的就是学习率。

学习的最终目的是为了将残差降低。或者说，BP算法的最终目标是要最小化整个训练集D上的累积误差。

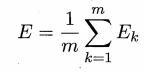
BP的求解过程关键词应该有四个：权值更新，梯度项计算，学习率

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！