HENAU 冬令营 搜索专题
A 棋盘问题
在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放k个棋子的所有可行的摆放方案C。
Input
输入含有多组测试数据。
每组数据的第一行是两个正整数,n k,用一个空格隔开,表示了将在一个n*n的矩阵内描述棋盘,以及摆放棋子的数目。 n <= 8 , k <= n
当为-1 -1时表示输入结束。
随后的n行描述了棋盘的形状:每行有n个字符,其中 # 表示棋盘区域, . 表示空白区域(数据保证不出现多余的空白行或者空白列)。
Output
对于每一组数据,给出一行输出,输出摆放的方案数目C (数据保证C<2^31)。
Sample Input
2 1 #. .# 4 4 ...# ..#. .#.. #... -1 -1
Sample Output
2 1
我觉得是简化版的八皇后问题
#include
#include
int num,d,n,k;
char a[100][100];
int vis[100];
void dfs(int i)
{
if(k==num)
{
d++;
return ;
}
if(i>=n)
return ;
for(int j=0;j
if(a[i][j]=='#'&&vis[j]==0)
{
vis[j]=1;
num++;
dfs(i+1);
num--;
vis[j]=0;
}
}
dfs(i+1);
}
int main()
{
while(scanf("%d %d",&n,&k)!=EOF)
{
num=0;
d=0;
if(n==-1&&k==-1)
break;
memset(vis,0,sizeof(vis));
for(int i=0;i
dfs(0);
printf("%d\n",d);
}
}
B-perket
你有 NN 种配料,每种配料有酸度 SS 和苦度 BB 。用这些配料做成Perket时,总的酸度为所有配料酸度的乘积,总的苦度是所有配料苦度的和。你至少需要添加一种配料。
为了使口感适中,总的酸度和苦度之差的绝对值应该尽可能小,求这个最小值。
输入
第一行 11 个整数 N \ (1\le N\le 10)N (1≤N≤10) —— 配料的数量。
接下来 NN 行每行 22 个整数 S_iSi 和 B_iBi —— 每种配料的酸度和苦度。如果用所有配料来做Perket,总的酸度和苦度都 \le 10^9≤109 。
输出
NN 行,每行 11 个整数 —— 所求的最小值。
| Sample Input 1 | Sample Output 1 |
|---|---|
1 3 10 | 7 |
| Sample Input 2 | Sample Output 2 |
|---|---|
2 3 8 5 8 | 1 |
| Sample Input 3 | Sample Output 3 |
|---|---|
4 1 7 2 6 3 8 4 9 | 1 |
#include
#include
int n;
int s[100],b[100];
int vis[100];
int sum,num;
int min=999999;
void dfs(int x)
{if(x>n)return ;for(int i=1;i<=n;i++){if(vis[i]==0){vis[i]=1;num=num*s[i];sum=sum+b[i];if(abs(num-sum) C-全排列
给定一个由不同的小写字母组成的字符串,输出这个字符串的所有全排列。 我们假设对于小写字母有 'a' < 'b' < ... < 'y' < 'z',而且给定的字符串中的字母已经按照从小到大的顺序排列。
输入格式
输入只有一行,是一个由不同的小写字母组成的字符串,已知字符串的长度在 11 到 66 之间。
输出格式
输出这个字符串的所有排列方式,每行一个排列。要求字母序比较小的排列在前面。字母序如下定义:
已知 S = s_1s_2...s_k, T = t_1t_2...t_kS=s1s2...sk,T=t1t2...tk,则 S < TS Sample Input Sample Output Select Code D-自然数拆分 对于任意大于 11 的自然数 nn,总是可以拆分成若干个小于 nn 的自然数之和。 现请你编写程序求出 nn 的所有拆分。 输入格式 输入文件共一行,包含一个自然数,即要拆分的自然数 n(1 \le n \le 20)n(1≤n≤20)。 输出格式 输出文件有若干行,每行包含一个等式,即代表一种可行的拆分(格式与顺序参见样例)。 Sample Input Sample Output 题意翻译 输入正整数 n,把整数 1,2,…,n 排成一个环,使得相邻两个整数之和均为素数。输出时,从整数 1 开始逆时针排列。同一个环恰好输出一次。n≤16,保证一定有解。 多组数据,读入到 第 i 组数据输出前加上一行 相邻两组输出中间加上一个空行。 输入样例 6 输出样例 Case 1: Case 2: 输出格式提示 行末无空格 Select Code F - Red and Black 有一个长方形的房间,覆盖了正方形的磁砖。每块磁砖的颜色,要么是红色,要么是黑色。一名男子站在一块黑色的磁砖上。他可以从一块磁砖移至相邻四块磁砖中的某一块。但是,他不允许在红色磁砖上移动,他只允许在黑色磁砖上移动。 输入 输入由多个数据集组成。数据集的起始行包含了两个正整数 W 和 H;W 和 H 分别是 x- 和 y- 方向的磁砖数量。W 和 H 不超过 20 。 输出 对于每个数据集,程序应当输出一行,包含他从初始磁砖所能抵达的磁砖数量 (包括初始磁砖自身)。 示例输入 示例输出 Select Code 题目描述 原题来自:POJ 1915 编写一个程序,计算一个骑士从棋盘上的一个格子到另一个格子所需的最小步数。骑士一步可以移动到的位置由下图给出。 输入格式 第一行给出骑士的数量 nn。 输出格式 对每一个骑士,输出一行一个整数表示需要移动的最小步数。如果起始点和终点相同,则输出 00。 样例 数据范围与提示 对于 100\%100% 的数据,有 4\le L\le 3004≤L≤300,保证 0\le x,y\le L-10≤x,y≤L−1。 Select Code H - Oil Deposits 某公司负责探测地下油层,每次处理一个大的矩形区域。先创建一个网格,将土地划分为许多方形块,然后用传感设备分别探测每个地块,以确定该地块是否含有石油。一块含有石油的土地叫做pocket。如果两个pocket边相邻或对角相邻,则它们属于同一油层的一部分。你的工作是确定在一个网格有多少不同的油层。 Input 输入包含多组数据。每组数据都以包含m和n的一行开始,m和n是网格中行和列的数量(1 <= m <= 100,1 <= n <= 100),由一个空格分隔。如果m = 0,则表示输入结束。下面是m行,每行有n个字符(不包括行尾字符)。每个字符对应一块土地,要么是“*”,代表没有油,要么是“@”,代表一个pocket。 Output 输出网格有多少不同的油层。 Sample Input Sample Output 0 Select Code I - Lake Counting 由于最近的降雨,农夫约翰的农田里形成了不同位置的水塘。农田被表示为一个矩形,它包含了 N x M (1 <= N <= 100; 1 <= M <= 100) 个小方格。每个方格中,要么包含了水 ('W'),要么包含了旱地 ('.')。农夫约翰想要弄清楚,他的农田中形成了多少个水塘。一个水塘是由包含了水的方格连通而成,这里一个方格被视作与周围的全部八个方格相邻。 输入 * 第一行:两个以空格分隔的整数: N 和 M 输出 * 第一行:农夫约翰的农田中,水塘的数量。 示例输入 示例输出 提示 输出细节: Select Code J - 二叉树先序遍历 输入一个整数n(n <= 100000),表示二叉树中节点个数,编号为1~n。约定1号节点为二叉树的根节点。然后输入n行,每行包括两个整数,第i行表示编号为i的节点的左子节点和右子节点的编号。如果某个节点没有左子节点,那么对应输行的第一个整数为0;如果某个节点没有右子节点,那么对应行的第二个整数为0。 先序遍历(DLR),是二叉树遍历的一种,也叫做先根遍历、前序遍历、前序周游,可记做根左右。前序遍历首先访问根节点然后遍历左子树,最后遍历右子树。 Input 第一行:一个整数n 接下来n行,每行有两个整数 Output 输出n行,每行一个整数,表示节点编号。 Sample Input Sample Output Select Code K - 迷宫(一) 一天蒜头君掉进了一个迷宫里面,蒜头君想逃出去,可怜的蒜头君连迷宫是否有能逃出去的路都不知道。 看在蒜头君这么可怜的份上,就请聪明的你告诉蒜头君是否有可以逃出去的路。 第一行输入两个整数 nn 和 mm,表示这是一个 n \times mn×m 的迷宫。 接下来的输入一个 nn 行 mm 列的迷宫。其中 输出一个字符串,如果蒜头君可以逃出迷宫输出 1 \le n, m \le 101≤n,m≤10。 Sample Input Sample Output Sample Input 2 Sample Output 2 #include 马在中国象棋以日字形规则移动。请编写一段程序,给定n*m大小的棋盘,以及马的初始位置(x,y),要求不能重复经过棋盘上的同一个点,计算马可以有多少途径遍历棋盘上的所有点。 Input 第一行为整数T(T < 10),表示测试数据组数。每一组测试数据包含一行,为四个整数,分别为棋盘的大小以及初始位置坐标n,m,x,y。(0<=x<=n-1,0<=y<=m-1, m < 6, n < 6) Output 每组测试数据包含一行,为一个整数,表示马能遍历棋盘的途径总数,0为无法遍历一次。 Sample Input Sample Output M - 八皇后问题 努比亚和苏丹没有子女,所以他要从一些有集成资格的继承者中挑选一个出来继承王位。他希望这个继承者足够聪明,所以他准备了一个西洋棋盘,上面的每个格子中均有一个 1-991−99 的数字。他又准备了 88 个皇后棋子。 88 皇后的规则就是不能有任何棋子同行或者同列或者同斜线,在满足这个规则的同时,王位继承者还需要让 88 个皇后所在的位置的数字的和是最大的。 输入一个数字 k(k\leq 20)k(k≤20),代表棋盘的数量。 接下来有 kk 个棋盘,每个棋盘有 6464 个数字,分成 88 行 88 列出入,具体可见样例,每一个数字均小于 100100。 每一个棋盘对应输出最大的数值, 一共输出 kk 行。 Sample Input Sample Output Select Code N - 选数 已知 nn 个整数 x_1,x_2,\cdots,x_nx1,x2,⋯,xn,以及一个整数 kk(k 3+7+12=223+7+12=22 3+7+19=293+7+19=29 7+12+19=387+12+19=38 3+12+19=343+12+19=34 现在,要求你计算出和为素数共有多少种。 例如上例,只有一种的和为素数:3+7+19=293+7+19=29。 输入格式为:nn,kk(1 \le n \le 20,k x_1,x_2,\cdots,x_nx1,x2,⋯,xn(1 \le x_i \le 50000001≤xi≤5000000)。 输出格式为:一个整数(满足条件的种数)。 Sample Input Sample Output Select Code O - 打开灯泡 Switch the Lamp On 达达是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女翰翰,从而被收留在地球上。 翰翰的家里有一辆飞行车。 有一天飞行车的电路板突然出现了故障,导致无法启动。 电路板的整体结构是一个R行C列的网格(R,C≤500),如下图所示。 每个格点都是电线的接点,每个格子都包含一个电子元件。 电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。 在旋转之后,它就可以连接另一条对角线的两个接点。 电路板左上角的接点接入直流电源,右下角的接点接入飞行车的发动装置。 达达发现因为某些元件的方向不小心发生了改变,电路板可能处于断路的状态。 她准备通过计算,旋转最少数量的元件,使电源与发动装置通过若干条短缆相连。 不过,电路的规模实在是太大了,达达并不擅长编程,希望你能够帮她解决这个问题。 注意:只能走斜向的线段,水平和竖直线段不能走。 Input 对于每组测试数据,第一行包含正整数R和C,表示电路板的行数和列数。 之后R行,每行C个字符,字符是"/"和"\"中的一个,表示标准件的方向。 Output 对于每组测试数据,在单独的一行输出一个正整数,表示所需的缩小旋转次数。 如果无论怎样都不能使得电源和发动机之间连通,输出NO SOLUTION。 Example 样例输入 样例输出 Hint 1≤R,C≤500, Select Code q;
int main() {scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) {scanf("%s",s[i]+1);}for(int i=1;i<=n+1;i++)for(int j=1;j<=m+1;j++)d[i][j]=-1;d[1][1]=0; q.push_back(make_pair(1,1));while(q.size()) {P now=q.front(); q.pop_front();if(now.ff==n+1&&now.ss==m+1) break;for(int i=0;i<4;i++) {int nx=now.ff+dx[i],ny=now.ss+dy[i];if(nx>=1&&nx<=n+1&&ny>=1&&ny<=m+1&&(d[nx][ny]==-1||d[nx][ny]>=d[now.ff][now.ss]+1)) {int xx=now.ff+bias_x[i],yy=now.ss+bias_y[i];if(s[xx][yy]==val[i]) {d[nx][ny]=d[now.ff][now.ss];q.push_front(make_pair(nx,ny));}else {d[nx][ny]=d[now.ff][now.ss]+1;q.push_back(make_pair(nx,ny));}}}}if(d[n+1][m+1]==-1) puts("NO SOLUTION");else printf("%d\n",d[n+1][m+1]);return 0;
} abc
abc
acb
bac
bca
cab
cba
#include5
5=1+1+1+1+1
5=1+1+1+2
5=1+1+3
5=1+2+2
5=1+4
5=2+3
E - Prime Ring Problem
EOF结束。Case i:
8
1 4 3 2 5 6
1 6 5 2 3 4
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
最后一个Case输出后不换行#include
编写一个程序,使得他允许重复上述的移动,判断他所能到达的黑色磁砖的数量。
在数据集中,还有 H 行,每行包含了 W 个字符。每个字符按如下方式表示一块磁砖的颜色。
'.' - 一块黑色的磁砖
'#' - 一块红色的磁砖
'@' - 一名男子,站在一块黑色磁砖上 (在一个数据集中,恰好出现一次)
以包含两个 0 的一行,表示输入结束。6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
11 9
.#.........
.#.#######.
.#.#.....#.
.#.#.###.#.
.#.#..@#.#.
.#.#####.#.
.#.......#.
.#########.
...........
11 6
..#..#..#..
..#..#..#..
..#..#..###
..#..#..#@.
..#..#..#..
..#..#..#..
7 7
..#.#..
..#.#..
###.###
...@...
###.###
..#.#..
..#.#..
0 0
45
59
6
13
#includeG - Knight Moves
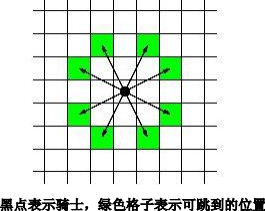
在接下来的 3n3n 行中,每 33 行描述了一个骑士。其中,Input Output 3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1
5
28
0
#include1 1
*
3 5
*@*@*
**@**
*@*@*
1 8
@@****@*
5 5
****@
*@@*@
*@**@
@@@*@
@@**@
0 0
1
2
2#include
给出农夫约翰的农田数据图,判断图中有多少个水塘。
* 第 2..N+1 行:每行 M 个字符,表示农夫约翰的农田中的一行。每个字符要么是 'W' 要么是 '.'。字符之间没有空格。10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
3
有 3 个水塘:一个位于左上方,一个位于左下方,还有一个位于右边。#include
先序遍历输出此二叉树每个节点的编号,每行输出一个编号。5
2 5
3 4
0 0
0 0
0 0
1
2
3
4
5
#include输入格式
'S' 表示蒜头君的位置,'*'表示墙,蒜头君无法通过,'.'表示路,蒜头君可以通过'.'移动,'T'表示迷宫的出口(蒜头君每次只能移动到四个与他相邻的位置——上,下,左,右)。输出格式
"yes",否则输出"no"。数据范围
3 4
S**.
..*.
***T
no
3 4
S**.
....
***T
yes
using namespace std;
int n,m;
int sx,sy,fx,fy;
int xx[4]={-1,1,0,0};
int yy[4]={0,0,1,-1};
int vis[15][15];
int f;
char s[15][15];
void dfs(int x,int y)
{
for(int i=0;i<=3;i++)
{
int dx=x+xx[i];
int dy=y+yy[i];
if(dx==fx&&dy==fy)
{
f=1;
return ;
}
if(1<=dx&&dx<=n&&1<=dy&&dy<=m&&vis[dx][dy]==0&&vis[dx][dy]!='*')
{
vis[dx][dy]=1;
dfs(dx,dy);
vis[dx][dy]=0;
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>s[i][j];
if(s[i][j]=='S')
sx=i,sy=j;
if(s[i][j]=='T')
fx=i,fy=j;
}
}
f=0;
dfs(sx,sy);
if(f==1)
cout<<"yes";
else
cout<<"no";
}
L - 马走日1
5 4 0 0
32
#include
#include
int n,m,x,y;
int d=0;
int temp[30][30];
int vis[8][2]={{-2,-1},{-2,1},{-1,2},{1,2},{2,1},{2,-1},{1,-2},{-1,-2}};
void dfs(int x,int y,int tep)
{
for(int i=0;i<=7;i++)
{
int xx=x+vis[i][0];
int xy=y+vis[i][1];
if((!temp[xx][xy])&&xx>=0&&xx
{
d++;
return ;
}
else
temp[xx][xy]=1;
dfs(xx,xy,tep+1);
temp[xx][xy]=0;
}
}
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
memset(temp,0,sizeof(temp));
d=0;
scanf("%d %d %d %d",&n,&m,&x,&y);
temp[x][y]=1;
dfs(x,y,2);
printf("%d\n",d);
}
return 0;
} 输入格式
输出格式
11 2 3 4 5 6 7 89 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
48 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64
260
#include输入格式
输出格式
4 3
3 7 12 19
1
#include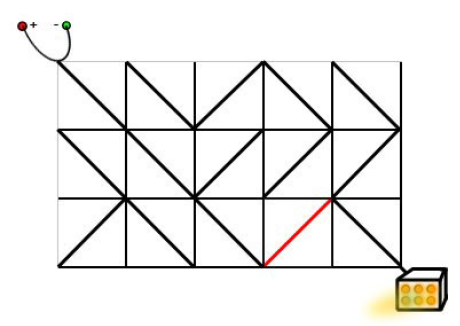
3 5
\\/\\
\\///
/\\\\1
1≤T≤5#include 本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!
