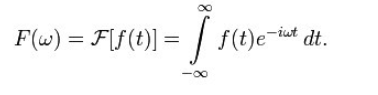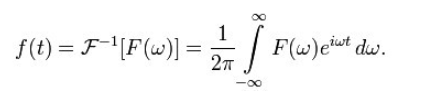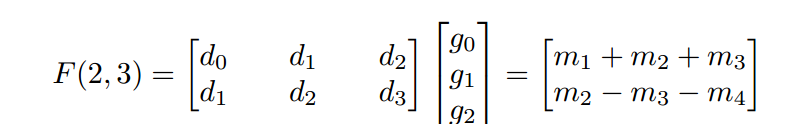一种快速卷积实现方法
本文基于论文Fast Algorithms for Convolutional Neural Networks,并且整理了相关知识点。
我们首先了解一下傅里叶变换:
对于连续型傅里叶变换的频域核时域转换公式:
对于离散的傅里叶变换:
关于傅里叶的理解 可以看这篇文章介绍 讲解的很好 https://zhuanlan.zhihu.com/p/19759362
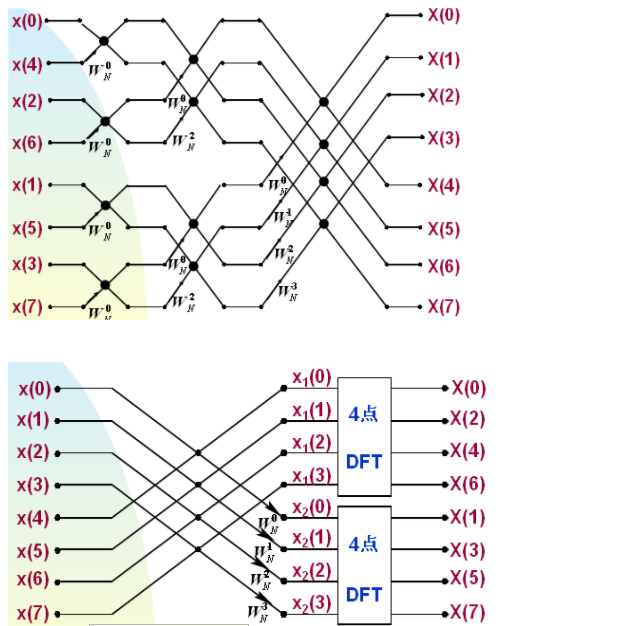
FFT是一种快速求解DFT的一种方法,我们在大学都学过,你可能忘记了,但是下面这个图是不是很熟悉
没错FFT的原理便是如此。在卷积的时候我们利用时域的卷积等于频域的相乘的结果去进行基于FFT的卷积操作。
我们知道当长度为r 的FIR滤波器得到一个长度为m 的输出的时候需要做m+r-1次乘法(F(m,r)),因而我们可以退出通过一个r*s大小的滤波器的时候我们得到m*n的输出,我们需要进行的计算(m+r-1)(n+s-1)次乘法(F(m*n,r*s))。
当我们计算F(2,3)
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!