【数模】方差分析
文章目录
- 单因素方差分析
- 简介
- 计算步骤
- SPSS操作步骤
- 结果分析
- 多因素方差分析
- 简介
- SPSS步骤
- 结果分析
单因素方差分析
简介
方差分析主要研究数据变异来源对总变异的贡献大小,从而确定变异是否是组间差异造成的。
适用条件:1.组内变量为连续数值型变量;2.组内变量符合正态分布;3.不同组方差必须相等。后两个条件可以适当程度减弱一些。
计算步骤
| SS | Df | MS | F | |
|---|---|---|---|---|
| 组间 | ∑ i = 1 n n i ( x i ˉ − x ˉ ˉ ) \sum_{i=1}^{n} n_{i}(\bar{x_{i}} - \bar{ \bar{x} } ) ∑i=1nni(xiˉ−xˉˉ) | m - 1 | S S 组间 / D f 组间 SS_{组间} / Df_{组间} SS组间/Df组间 | M S 组间 / M S 组内 MS_{组间} / MS_{组内} MS组间/MS组内 |
| 组内 | ∑ i = 1 n ∑ j = 1 m ( x i j − x i ˉ ) 2 \sum_{i=1}^{n} \sum_{j=1}^{m} (x_{ij} - \bar{x_{i}} ) ^2 ∑i=1n∑j=1m(xij−xiˉ)2 | n - m | S S 组内 / D f 组内 SS_{组内} / Df_{组内} SS组内/Df组内 |
其中,Df为自由度。
使用F值进行F检验可以计算出假设检验的P值。
此时的原假设为:不同组之间没有显著性差异。
备择假设为:至少有一对组之间存在显著差异。
SPSS操作步骤
这里选用鸢尾花数据,但只比较不同组数据(3组数据)的萼片宽度是否由组间差异造成。(手头暂无数据出此下策)
- 导入数据依次选择:分析->比较平均值->单因素ANOVA检验:
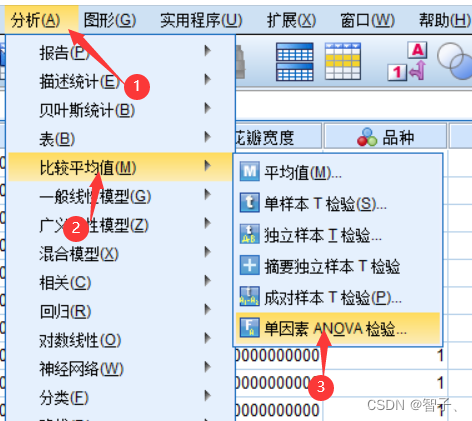
- 选择因子和因变量:
选择因子:
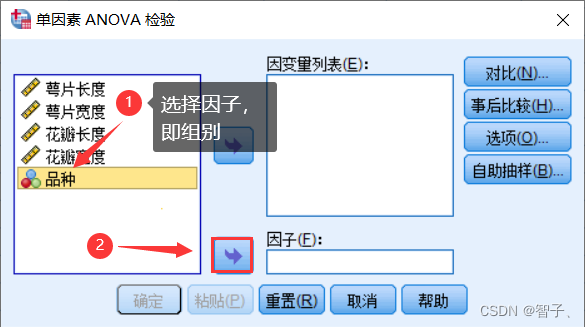
选择因变量(这里只选择萼片宽度):
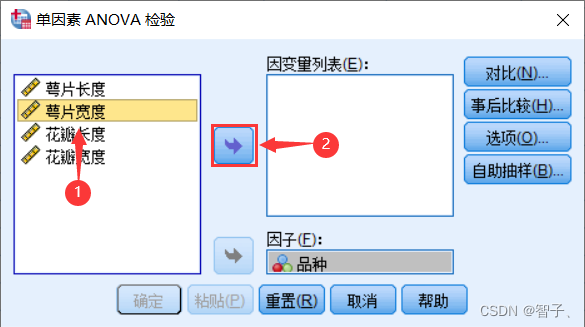
- 点击对比并进一步勾选:
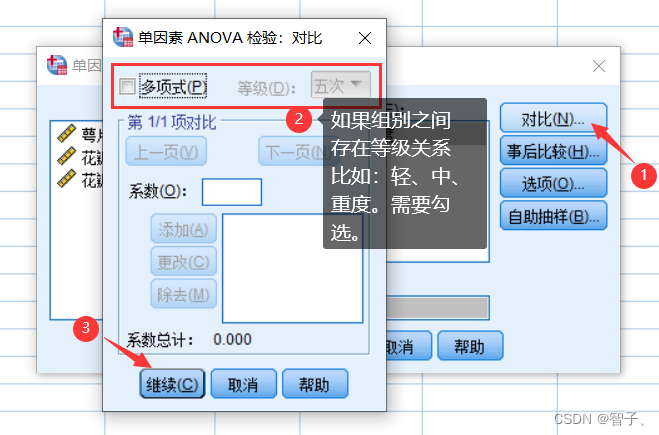
- 点击事后比较并进一步勾选:
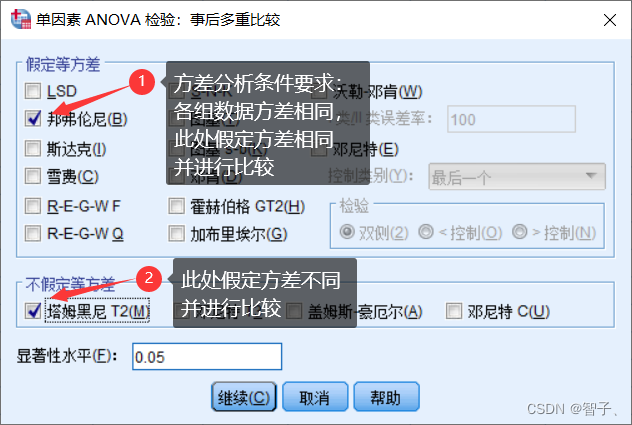
- 点击选项并进一步勾选:
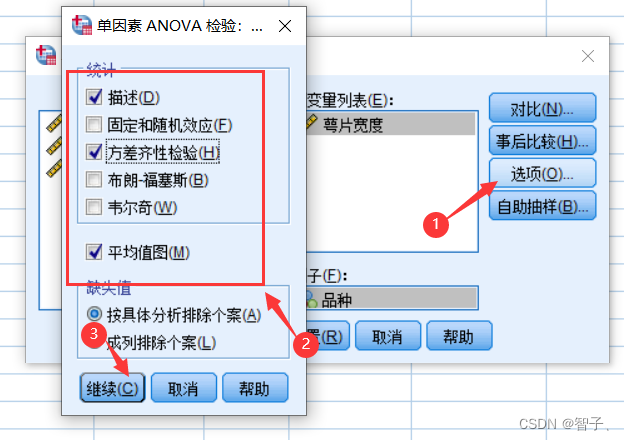
- 点击确定,输出结果。
结果分析
-
方差奇性检验:
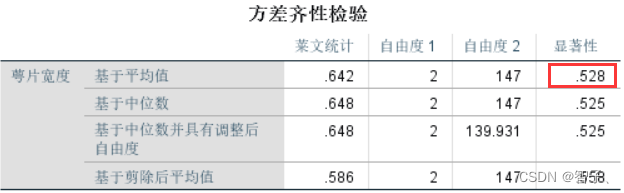
此处,方差在90%的置信水平上保持一致。注意:方差齐性检验不通过的话方差分析就失败了。 -
方差分析结果
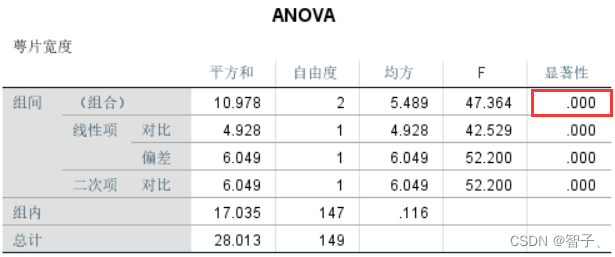
红框包围的区域即:方差分析的结果P值等于0.000。说明在99%的置信水平上拒绝原假设,即拒绝不同组之间没有显著性差异。 -
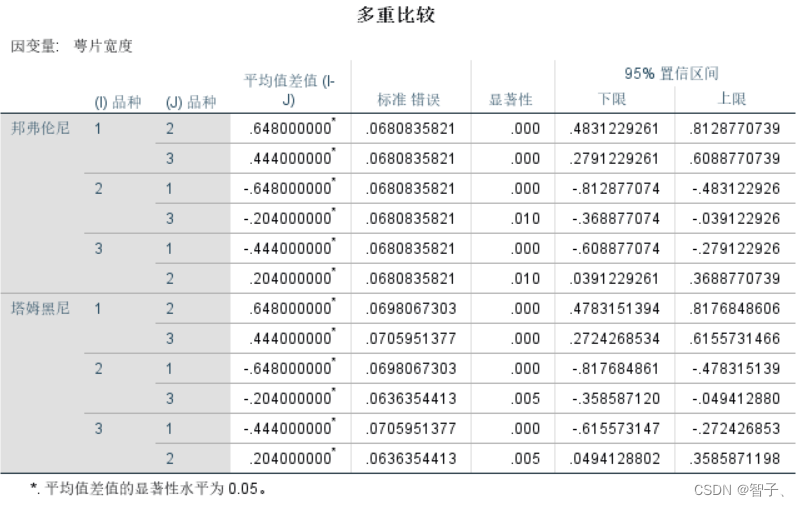
事后比较:
即不同组别两两比较的结果,可以得到两两之间是否存在显著差异。注意:方差齐性检验通过看邦费伦尼子表,不通过看塔姆黑尼子表。
多因素方差分析
简介
当有两个或者两个以上的非数值型因素对数值型因变量产生影响时,可以用多因素方差分析的方法来进行分析。
多因素方差分析亦称“多向方差分析”,原理与单因素方差分析基本一致,也是利用方差比较的方法,通过假设检验的过程来判断多个因素是否对因变量产生显著性影响。
在多因素方差分析中,由于影响因变量的因素有多个,其中某些因素除了自身对因变量产生影响之外,它们之间也有可能会共同对因变量产生影响。在多因素方差分析中,把因素单独对因变量产生的影响称之为“主效应”;把因素之间共同对因变量产生的影响,或者因素某些水平同时出现时,除了主效应之外的附加影响,称之为“交互效应”。多因素方差分析不仅要考虑每个因素的主效应,往往还要考虑因素之间的交互效应。此外,多因素方差分析往往假定因素与因变量之间的关系是线性关系。从这个方面来说,方差分析的模型也是如下一个一般化线性模型的延续:因变量=因素1主效应+因素2主效应+…+因素n主效应+因素交互效应1+因素交互效应2+…+因素交互效应m+随机误差。所以多因素方差分析往往选用一般化线性模型(General Iinear Model)进行参数估计 。
SPSS步骤
这里选择性别和是否使用手机对驾车得分的影响来分析。
- 导入数据并依次点击:分析->一般线性模型->单变量:
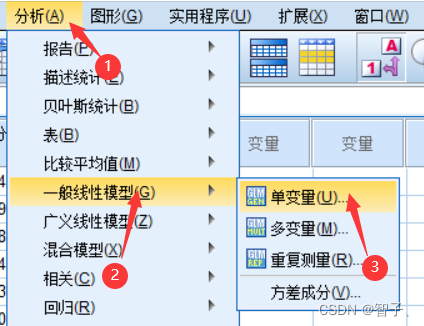
- 设置因变量和组数:
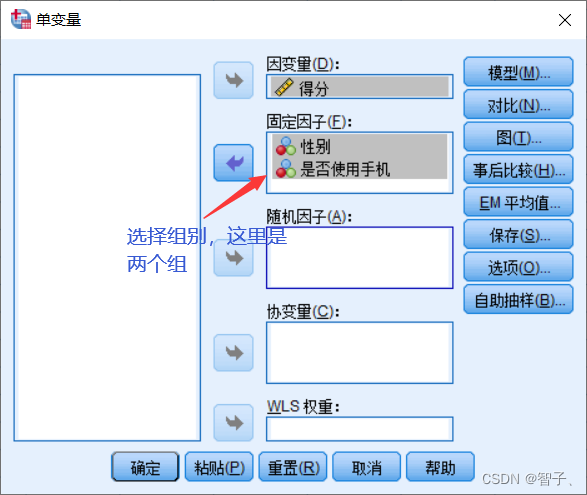
- 作图:
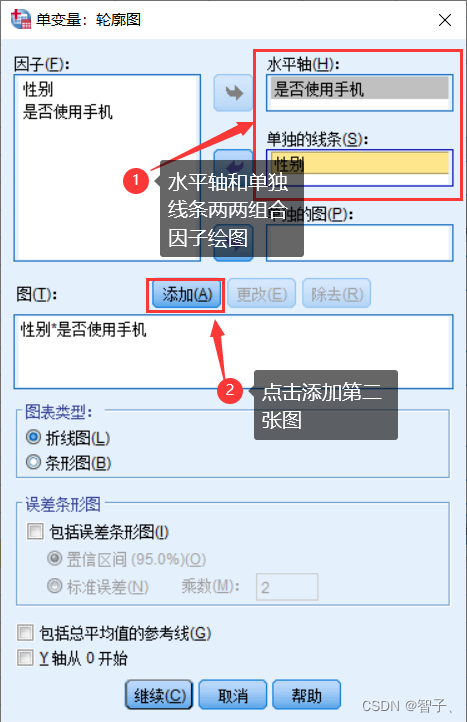
- 估计因子效应量:
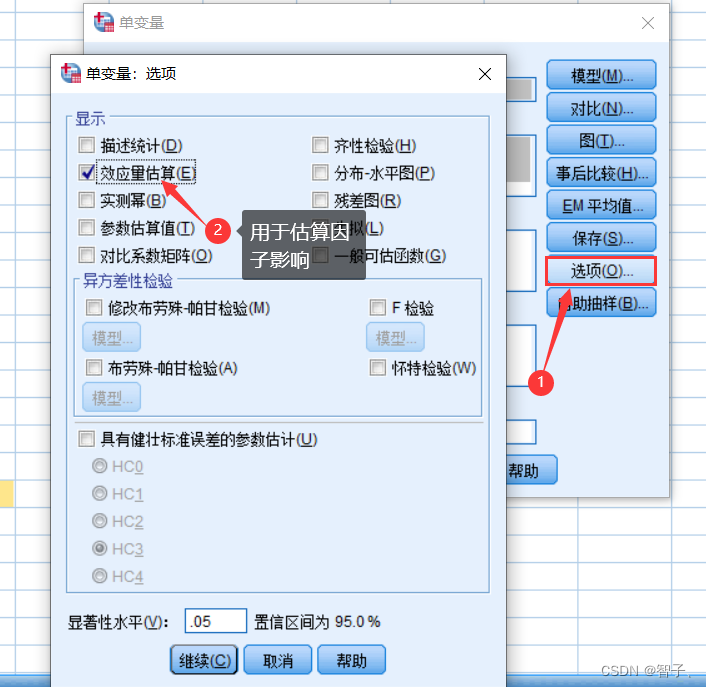
- 点击确定并输出结果。
结果分析
- 效应量分析:
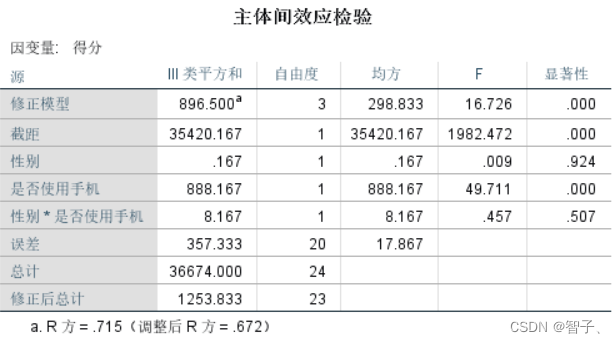
由表得:性别对得分影响不显著,而是否使用手机在99%的置信水平上影响得分。 - 图分析:
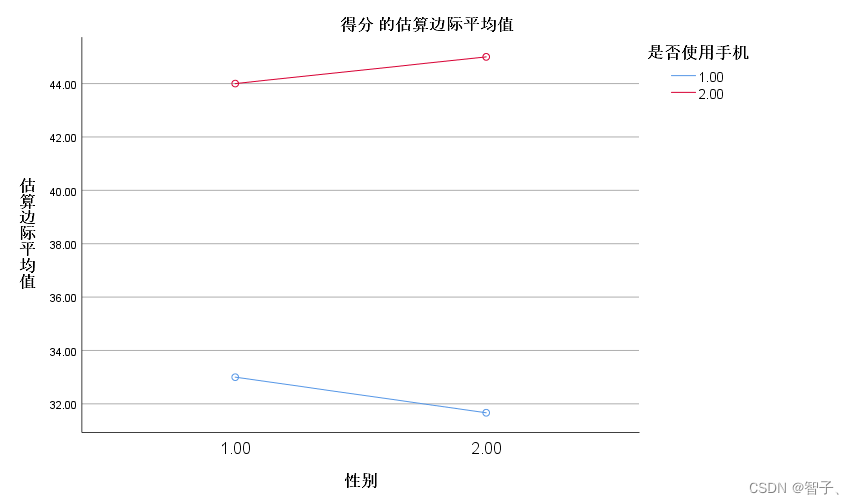
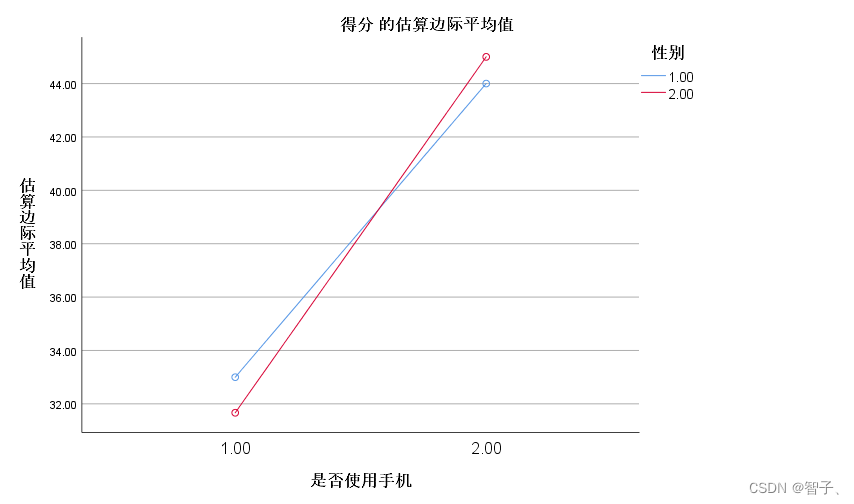
图和表结论基本一致。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!