集合论与图论期末复习
难记知识点分章节
图论：
图的基本概念
1.导出子图：//由顶点导出
设S为图G=(V,E)的顶点集V的非空子集,
则G的以S为顶点集的极大子图称为由S导出的子图,记
为
迹：各边不同的通道；路：顶点不同的通道
定理6.3.2 设G=(V,E)是一个有p个顶点的图, 若对G 的任两个不邻接的顶点u和v:degu+degv≥p-1 ,则G 是 连通的 。 定理6.3.3 设G=(V,E)是至少有一个顶点不是弧立 顶点的图, 如果对于任意 u属于 V,degu为偶数,则G中有圈。 3.偶图定义：顶点集V有一个二划分{V1,V2}；使得G的任一条边的两个端点一个在V1中，另一个在V2中。 偶图充分必要条件：所有圈长都是偶数长 4.欧拉图当且仅当G是连通的且每个顶点的度都是偶数 ->图G有一条欧拉开迹当且仅当G是连通的且仅有两个奇度顶点 2n个奇度顶点，n>=1，则G的全部边可以排成n条开迹，且至少有n条开迹 
5.哈密顿图的性质：G（V,E）
- 对V的每个非空子集S，均有w（G-S）<=|S|
- 定理6.6.2 （Dirac)p个顶点，p>=3,如果顶点最小度数>=p/2，则G是一个哈密顿图
- ->任意一对不邻接的顶点u和v均有degu+degv>=p-1，则G有一个哈密顿路或生成路
树和割集
1.树：连通且无圈的无向图 <=> 连通且p=q+1 <=> 无圈且p=q+1；
- 树--极小连通图
- 顶点偏心率（连通图G（V,E））：e（v)=max{d(v,u)}(u∈V）
- 半径：min{e(v)}
- 非平凡树是偶图->可用两种颜色染色
2.生成树 G（V,E）
- 生成子图T=（V,F）
- G有生成树的充分必要条件<=>是一个连通图
- 任意图都有生成森林
- 具有p个顶点的完全图Kp有p的p-2次方棵生成树
- 最小生成树不一定唯一
- Kruskal算法：依次取出现有图中最小权的边直至最后生成树
- prime算法：任取一个点，选最小权边，再选这多加的一个点的最小权的边
割点、桥和割集
- 割点/桥：G-v/G-x的支数大于G的支数
- 最长路的两个端点不是割点
- 割集S：去掉S中所有边得到的G-S支数大于G支数，去掉S任一真子集中的边，支数不大于G支数
连通图和匹配
k（G）<=入（G）<=顶点最小度
平面图与图的着色
V-E+F=2->p-q+f=2
平面连通图G，每个面由长为n的圆圈围成->q=n(p-2)/(n-2)
->G是最大可平面图：q=3p-6；每个面都是长为4的圆圈围成：q=2p-4
->K5与K3，3都不是可平面图
->顶点度最小值<=5
- k个支平面图：p-q+f=k+1
- G是顶点数p>11的平面图，G的补图不是平面图
错题
1.在边长为 1 的等边三角形内任意放置一些点，要使得至少存在 2 个点之间距离不超过
1/n 那么至少应该放几个点 （） 答： n^2+1 把等边三角形的每一边分为n份 每两个点之间连线，则把三角形分为n^2个相同大小的三角形，分布在各个三角形里的点距离都不超过1/n，则至少要放n^2+1个 2.设 f:X→Y。X 和 Y 为有穷集合。如果 f 是左可逆的，那么 f 有多少个左逆映射？( |X|^(|Y|- |X|) ） 3.设 f：X→Y，C ⊆Y ， D⊆Y 。则 f -1 （ C\D ） =f -1 （ C ） \f -1 （ D ） 正确！ 4.有理数和自然数一样多 有理数是可数集！ 5. 证明 n 个人参加会议至少有两个人认识的人数是一样的 答： 这n个人认识的人数的情况最多有n-1种情况 ，由抽屉原理，至少有两个人认识的人数相同。 6.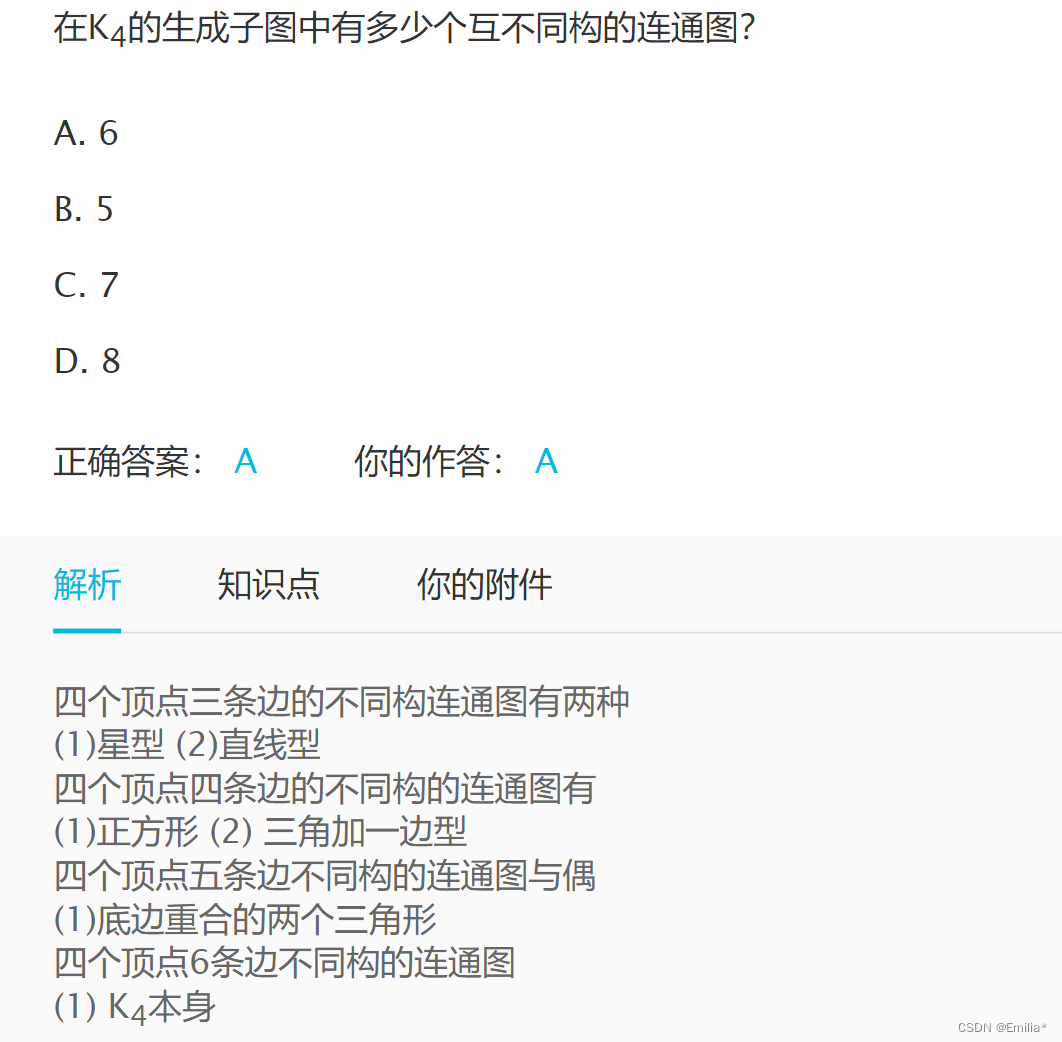
//数生成图中互不同构的连通图的个数可以按边数从小到大依次数，不会漏
7.K3，3至少需要三笔画画成
/*有6个奇度顶点，所以至少可以3笔画。欧拉闭迹要求包括所有的顶点和边，所以每个顶点的度一定是偶数，奇度顶点只能是出现在欧拉开迹两端，所以2*n个奇度顶点-->n条欧拉开迹*/
8.K5存在欧拉闭迹；K5，5没有欧拉闭迹//前者每个顶点度为偶数，后者每个为奇数
9.
n笔画-->2n个奇度顶点；能一笔画-->是欧拉图||连通&&只有两个奇度顶点
10.
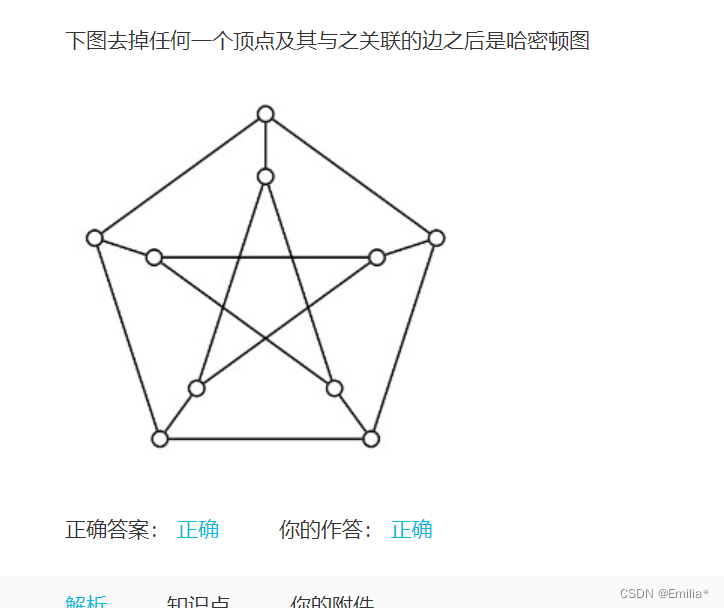
哈密顿图：哈密顿圈，要包括所有点，不用所有边
11.哈密顿图需要特殊记忆：
- 去掉顶点后支数小于等于去掉的顶点数
- 能染色且两种颜色顶点数相同-->推论：Km，n是哈密顿图则m=n
12.哈密顿路：3个1度顶点肯定没有哈密顿路
13.哈密顿圈：
14.
15.顶点最小度>=p/2是判断是哈密顿图的充分不必要条件
16.
17.
18.
19.
零碎知识点✌
1.关系的合成与映射的合成写法和运算是不同的！
没有问题！就是按顺序合成！
2.正五边形的补图为五角星，而且他们同构
3.关系闭包等记法：
自反闭包：r（R）
对称闭包：s（R）
4.集合的（ 描述）表述方法能够引起悖论
5.映射是一种特殊的关系
6.求传递闭包的过程：
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！